基于BP神经网络的学生综合考评预测研究
冯相榕 李鹏 孟旭莹
摘要:为探究传统成绩评定模型与综合考评模型的不同,以及对学生最后成绩进行科学准确地预测,提出通过搭建神经网络,基于Code Blocks和Matlab平台,运用BP算法分别对传统成绩评定模型和综合考评模型进行预测分析。结果表明,使用神经网络算法预测成绩的正确性及有效性,并对比得出使用综合考评模型预测时,对学生的评估效果更优。
关键词:神经网络;BP算法;成绩预测模型;综合素质教育
中图分类号:TP301.6文献标志码:A文章编号:1008-1739(2019)20-65-4

0引言
目前部分高校的綜合考评制度存在一些问题,在秦非[1]的研究中,针对目前综合考评体系存在的问题提出了相应的改进措施。以往的工作中,普遍采用通过各项成绩占比进行算术运算的方式,得出学生最终综合考评成绩。据调研,目前已有基于机器学习、对话流、数据挖掘和卡尔曼滤波算法等方法对成绩进行预测的研究。本文主要利用已知的传统测评方式及综合测评方式,结合BP神经网络模型得出学生最终综合考评成绩。BP神经网络能通过反复学习,将大量已知的匹配输入量和输出量及其映射关系保存下来,而不需要提供相应的数学方程,通过学习训练样本发掘映射关系。通过神经网络搭建的模型具有自组织自学习性、便捷性、有效性和容错性等优点。通过此模型预测出学生的综合考评成绩与学生实际综合考评成绩是相拟合的。
1反向传播神经网络
1.1网络拓扑结构
神经网络分为输入层、输出层和隐藏层[2]。同一层的神经元之间没有连接,相邻2层之间有连接,每一个连接均具有一个权值。不同的神经网络中,连接规则不同。例如,在全连接神经网络中,第-1层神经元的输出是第层神经元的输入,第-1层的所有神经元和第层的每个神经元相连。除此之外,还有很多不同的神经网络,如卷积神经网络(CNN)、循环神经网络(RNN)等。
基于ConvNetJS平台对神经网络的立体结构进行模拟,如图1所示。
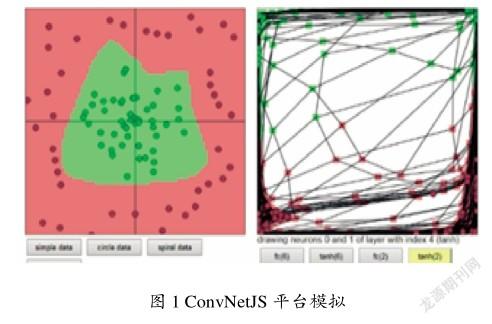
该神经网络可将数据简单分成2类。通过模拟,发现神经网络可为处理数据而变换坐标空间,降低维度,也可以升高维度;可以变成圆形,也可以变成方形;可以放大,也可以收缩。
1.2 BP算法
1.2.1基本思想
学习规则采用有导师学习的连续感知器规则,学习过程由信号的前向传输和误差的逆向反馈构成。
前向传输过程中,逐层波浪式地传递输出值。将输入样本传入输入层,经过每个隐藏层计算和处理,在输出层传出[3]。当输出层的期望值与实际输出值有偏差时,进入误差的反向传播阶段。
逆向反馈过程中,将实际输出经过隐藏层反馈给输入层,以将误差划分到各层,从而得到各部分的误差信号,即得到对每层调整的依据[4]。依此,对每层的权重及偏置进行修正。
1.2.2伪代码

2模型建立
2.1传统成绩评定模型
2.1.1理论模型
学生素质综合测评实行百分制,考评内容分为平时成绩与期末卷面成绩,传统成绩评定模型如表1所示。

2.1.2神经网络模型
利用随机函数产生800组同学的数据样本,各项成绩作为输入,即平时成绩与卷面成绩,所以输入层选用2个神经元,隐藏层选用6个神经元,输出层选用1个神经元将对应的期末成绩输出。利用Neural Network Playground平台对模型架构进行模拟,如图2所示。

2.2综合考评评定模型
2.2.1理论模型
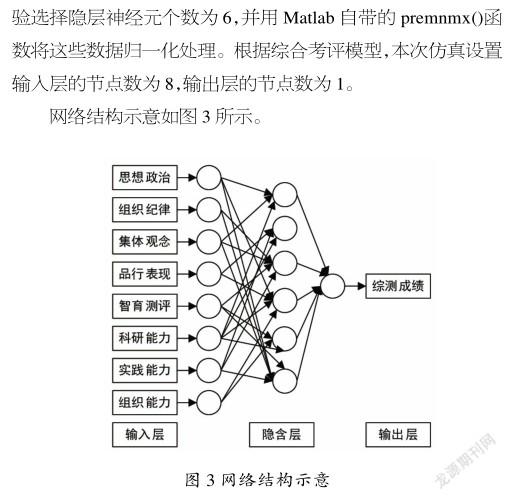
将前14组同学各项成绩作为输入,对应的综测成绩作为输出。其中,思想政治、组织纪律、集体观念和品性表现各占总成绩的2.5%,智育成绩占总成绩的80%,科研能力占总成绩的5%,实践能力占总成绩的4%,组织能力占总成绩的1%。
2.2.2神经网络模型
实验采用单隐层的神经网络模型,即3层多输入单输出。搭建神经网络时,假如隐层网络神经元个数过多,则会导致机器运算量直线上升,造成结果过度拟合;过少又会给运算结果带来较大偏差,难以得到预期结果。
因此,隐层网络神经元个数的确定与实际问题息息相关,并且与输入层及输出层神经元个数及设定的期望误差值等因素都有关系。在建模过程中,使用下面的公式确定隐层网络神经元个数[5]:

2.3学习过程建模
建模过程中,采用的激活函数是Sigmoid函数(S函数)。在输入层中,归一化样本数据,初始化偏置与权值,使BP神经网络的收敛速度变快,训练效率得到有效提升[6]。反馈调节从输出层开始逆向进行修正网络的权重值和偏置值,按权重累加隐藏层通过下一层的所有结点的误差,计算出误差率之后,根据误差率的值,对偏置值和权重进行修正,更新偏置,对整个网络的平均误差进行记录,当与其设置的训练精度一致时,停止训练。
3模型训练与结果
3.1传统成绩评定模型
基于Code Blocks平台,采用C语言编写程序,对模型进行仿真。训练代码如下:

该部分是BP神经网络的反馈学习的核心,将实际预测结果与样本預期的结果进行对比,然后对网络中各层各单元涉及的权重进行逐层修正。
3.2综合成绩评定模型

该部分是核心代码,完成了从样本数据归一化、创建神经网络、设置相关参数和进行测试等全过程。
4预测与分析
4.1传统成绩评定模型预测
手动给定数据进行期末成绩的预测,结果如图4所示。

比较预测成绩和期望成绩可知,在进行了314次训练之后,通过神经网络进行预测的成绩与期望成绩相差在0~0.6之间。
4.2综合模型预测
测试数据对比结果如图5所示。
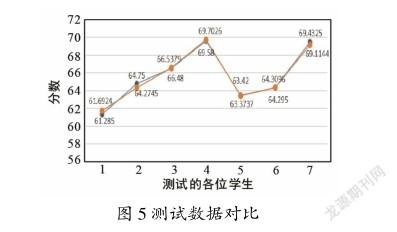
首先对样本数据进行归一化处理,将归一化后的数据输入网络。然后根据输入层及输出层神经元个数确定隐层神经元的个数为6[9]。设置神经网络中输入层、隐藏层和输出层的激励函数分别为tansig,tansig,purelin函数,将traingdx函数设置为神经网络的训练函数,并设置学习速率等网络参数。最后对数据进行反归一化进行输出。本次采用Matlab平台的神经网络工具箱对搭建的神经网络进行训练[10],从实验结果来看,通过神经网络进行预测的成绩与期望成绩相差在0.04~0.5之间。
5结束语
针对目前高校教育中广泛关注的成绩评估问题,进行了仿真实验与验证。发现了综合素质教育及评定在目前大学教育中仍旧是非常重要的,所以学校在加强文化课的同时要积极拓展素质教育。实验基于Code Blocks和Matlab平台,实现了关键算法,并将传统成绩评定模型和综合考评模型结合,对最终成绩开展预测,证明了算法的正确性和有效性。
参考文献
[1]秦非.论高校综合考评积分实施细则[J].陕西师范大学学报(哲学社会科学版),2008,37(S2):142-144.
[2]孙文.基于深度学习模型的感应电机故障诊断方法研究[D].南京:东南大学,2017.
[3]贺清碧.BP神经网络及应用研究[D].重庆:重庆交通学院, 2004.
[4]吴涛.车型识别系统的设计与实现[D].桂林:广西师范大学, 2011.
[5]韩航星,王金全,方建华,等.全钒液流电池SOC估算方法研究[J].电源技术,2017,41(4):661-664.
[6]薛航.神经网络用于地基辐射计大气参量反演算法研究[D].武汉:华中科技大学,2016.
[7]张方.基于BP神经网络的税收预测研究[D].西安:长安大学,2016.
[8]肖霜.神经网络方法在收益法参数确定中的应用[D].重庆:重庆理工大学,2016.
[9]韩少波,邵婷婷.基于BP神经网络的油井井斜角误差补偿研究[J].内蒙古石油化工,2015,41(1):37-38.
[10]郭凌云.基于RBF神经网络的液体细分器的设计[D].北京:北京邮电大学,2013.

