高空薄膜相机设计参数优化
付慧 唐园亮 毛力奋 蒋光南 王普勇 原力
摘要:文中通过对高空薄膜相机进行有限元计算,获得在初始设计变量条件下薄膜相机的变形量,并以此作为在EMT优化平台中的初始数据,采用超拉丁方程计算,以薄膜相机的最大变形量为目标函数,以弹性模量与薄膜材料厚度为约束条件,对薄膜相机进行结构优化设计,得到多组优化方案,为设计人员进行结构设计提供7有用的信息及多种设计方案的选择。
关键词:薄膜相机 EMT平台 有限元分析 参数优化
引言
为解决传统反射式空间光学系统在口径增大时面临的重量和拼接精度要求高的难题,提出了将微结构亚波长光学元件应用于空间光学成像系统中。使用透射的微结构亚波长光学元件作为空间光学系统的主镜以及其它光学元件有两个特有的优势,可以同时克服反射系统所遇到的困难宽松的面形公羞重量轻、结构灵活,便于运输和部署。
1薄膜相机模型及工况
l.1材料属性
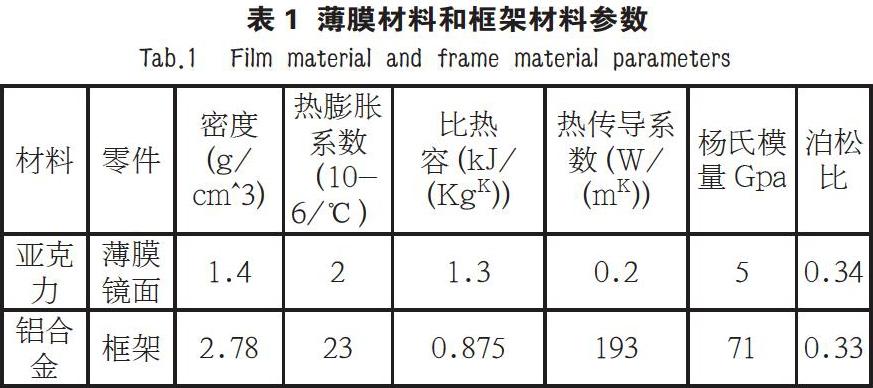
薄膜相机结构有两种材料,包括亚克力(薄膜镜面材料)和铝合金(框架材料)。如表1所示为薄膜材料和铝合金材料的参数。
1.2薄膜相机模型参数
薄膜相机结构:薄膜相机由薄膜和框架组成:薄膜相机的CAD模型如图l所示,薄膜厚0.5mm,直径440mm;框架厚度20mm,内径400mm,外径440mm。薄膜与框架的接触部分采用的是环向粘接装配。
1.3薄膜相机工况及要求
研究薄膜相机的载荷工况是:在相机水平放置时只考虑重力作用下薄膜相机的变形情况。
·重力作用下的变形
·透镜水平放置
镜头成像要求:薄膜相机在受重力载荷时,会产生变形量,最大变形量在薄膜镜片上,但是为了满足相机视场、焦距等要求,薄膜镜片的变形量为:
变形量≤2.5mm
影响薄膜镜片性能的因素有很多,如:弹性模量、材料密度、薄膜材料厚度等等,此处考虑薄膜密度不变,只考虑弹性模量与薄膜材料厚度对变形量的影响。
2模型参数优化及方案对比
2.1结构参数优化的数学模型
基于高空薄膜相机的工作要求,建立如下的数学模型。
目标函数:
f(x)≤2.5
约束条件:
4000≤g(x)≤6000
0.4≤h(x)≤0.6
其中f(x)为最大变形量(单位mm)g(x)为弹性模量:单位MPal单位mm),h(x)为薄膜材料厚度(单位mm)。
o.o优化流程
首先将初始数据输入EMT平台中,在集成的CAD软件中建模,之后将建立好的模型导入网格划分求解器中进行网格划分,得到CAE模型并在EMT平台集成的有限元软件中进行仿真分析,得到初始输入参数下薄膜相机结构的最大变形量,然后将仿真结果导入优化模块中进行优化计算,再以优化结果进行循环计算。
2.3优化结论
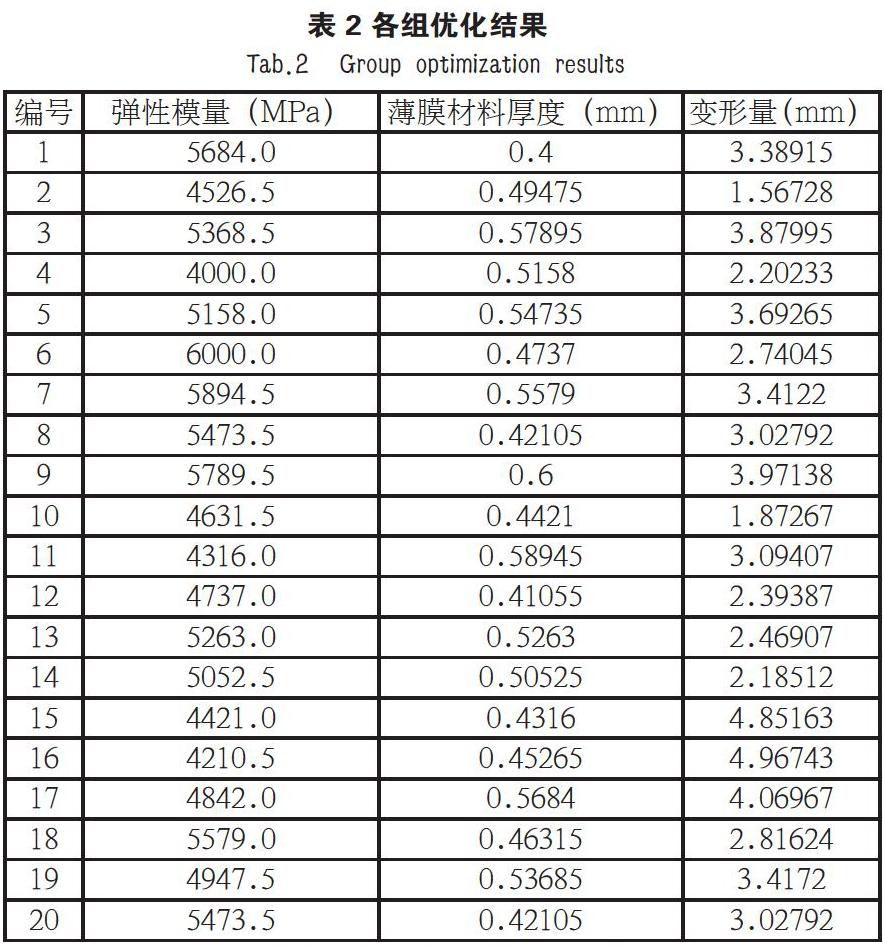
设定20种优化方案,得到如表2所示的优化方案。
要考虑高空材料对重量和材料属性的要求,最终选择第14组数据,确定的最优化参数:薄膜材料厚度为0.5mm,弹性模量为5052.5MPa,对应的薄膜最大变形量为2.2mm。
本文针对高空薄膜相机的初步设计结构进行了更深一步的轻量化优化研究,给薄膜相机的轻量化工作作了很好的探索。研究中,首先对薄膜和框架结构形式作了重新考虑,选用了亚克力作为基材進行制作,降低了薄膜相机的重量;然后利用EMT技术优化其结构尺寸,以改善薄膜变形;最后,通过比较得到了薄膜相机的最优化设计方案。该方案兼具经济、适用的优点,满足设计要求。
参考文献
[1]王松,应用于空间光学的聚合物薄膜性能研究[D],中国科学院研究生院(光电技术研究所),2016.
[2]王瑞.亚克力替代TAC的现状与未来[J],信息记录材料,2014,15(06):45-48.
[3]余金宝,范元勋.基于Isight和ABAQUS软件的柔轮筒体应力与结构优化[J],机械制造,2018,56(11):60 63.
[4]孙荣阁,易葵,范正修,真空镀膜中基底预应力的有限元分析[J].中国激光,2006,33(7).

