基于功效散度和成对约束的半监督聚类算法

向思源，金应华，徐圣兵

（广东工业大学应用数学学院，广东广州510520）

在当今大数据时代,信息技术迅猛发展，极大地提高了数据收集和存储能力，各个领域都积累了海量的数据，促使数据处理技术得到广泛应用。聚类分析属于机器学习和数据挖掘领域的经典课题，是数据处理的主要工具之一。传统的聚类算法是一种典型的无监督学习，例如K-均值（K-means）算法［1］、模糊 C 均值（Fuzzy C-means，FCM）算法［2］和极大熵聚类（Maximum Entropy Clustering，MEC）算法［3］等。MEC算法是在FCM算法的目标函数中加入信息熵惩罚项，利用最大熵原理，使得聚类结果更符合实际。针对各类背景复杂的实际应用问题，已有多种MEC算法的变种［4-10］。相对于无监督学习，有监督学习也是数据处理常用方法之一，两种方法的本质区别是后者已有训练集，对训练集进行建模的方法有很多，例如支持向量机、线性判别分析、K-近邻、神经网络和决策树等［11］。

一般地，实际数据既含有大量未标记的样本，也含有少量已标记样本或少量样本的类关系信息。无监督学习和有监督学习分别利用未标记样本和已标记样本（训练集）进行建模，但两者都不能有效分析包含类关系信息的聚类分析问题。针对这一缺陷，半监督学习方法应运而生，并得到快速发展。半监督学习能有效利用少量已知样本的类关系监督信息，提高聚类算法的性能。根据监督信息形式，半监督聚类方法可分为以下两类。

（1）监督信息为少量已标记类别样本。聚类算法利用这部分标签信息来引导聚类过程，以期得到更好的聚类结果［12-15］。近年来，此类半监督聚类有向高维数据发展的趋势［16］。另，此类基于少量已标记类别样本半监督聚类方法与本文的研究内容联系甚少。

（2）监督信息为成对约束，即样本对之间的类关系信息。成对约束是一种普遍存在且应用广泛的数据信息，因此基于成对约束的半监督聚类研究具有十分重要的实际意义［17-29］。该类研究的基本框架是以MEC算法为基础，加入成对约束对应隶属度的惩罚项，用它表示成对约束的信息。现有文献中，已有多种基于成对约束的半监督聚类方法，例如竞争凝聚态算法［17］、基于贝叶斯先验理论的概率方法［18-19］、基于谱分解的聚类方法［26-29］等。

在聚类分析领域，可以利用交叉熵刻画样本对之间的成对约束信息，并且以此来构造聚类分析方法［30-34］。李晁铭等［34］用样本交叉熵描述样本自信息与成对约束信息，提出了基于成对约束的交叉熵半监督聚类算法（Cross-Entropy Semi-supervised Clustering Based on Pairwise Constraints，CE-sSC）。CE-sSC算法是MEC算法在半监督学习领域中的一种推广形式。

本文在文献［34］研究结果的基础上，提出了一类半监督聚类算法。该算法剔除了CE-sSC算法中交叉熵之间的重复部分，避免了各熵项之间的相互干扰，使得惩罚项系数的选择简单明了。新算法推广了惩罚项的形式，提供了一族选择，包含相对熵特例。实证分析表明，在成对约束较少时，新算法具备良好的聚类性能；与CE-sSC算法相比，惩罚系数的选择更简洁高效。

1 算法

1.1 原理

MEC算法有收敛速度快、数值稳定性好、容易实现等优点，缺点是其中的惩罚项（信息熵）仅能表达样本点属于同类的自身性的自信息（Self-information），即各样本自身的内部信息。信息熵定义如下。

定义1设样本点xj的隶属度向量为μjT（μ1j，…，μcj），其中T为转置符号，c为聚类数。称

为样本点xj的信息熵。

信息熵仅含有各样本自身的内部信息［34］。当数据带成对约束时，就需要构造新的惩罚项。成对约束是不同样本之间的类关系信息，要求新的惩罚项能够充分利用此类信息。一般采用的成对约束为must-link约束类和cannot-link约束类，具体定义如下。

定义 2 must-link 集合 ML=｛（xj，xk）│j＜k｝，若（xj，xk）∈ML，则表明xj和xk必须属于同类，也称xj和xk存在正关联约束关系。

存在正关联约束关系的样本对xj和xk包含信息如图1所示，其中实线圈代表类簇，小三角形代表样本点，同一实线圈中的样本点属于同一类簇，灰色小三角形代表样本点xj，黑色小三角形代表样本点xk·xj和xk属于同一类簇cluster1，即存在正关联约束关系。

定义 3 cannot-link 集合 CL=｛（xj，xk）│j＜k｝，若（xj，xk）∈CL，则表明xj和xk必须属于不同类簇，也称xj和xk存在负关联约束关系。

存在负关联约束关系样本对xj和xk包含信息如图2所示，其中实线圈和小三角形的含义同图1，不同实线圈中样本点属于不同类簇，灰色小三角形代表样本点xj，黑色小三角形代表样本点xk·xj和xk分别属于类簇cluster1和类簇cluster2，即存在负关联约束关系。

在正关联约束和负关联约束的直观意义下，李晁铭等［34］借用交叉熵，构造了CE-sSC半监督聚类算法。该算法推广了传统MEC算法中的惩罚项（信息熵），使其能充分利用成对约束信息。

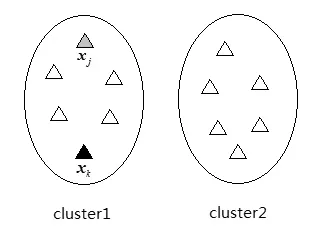
图1 正关联约束关系样本点示意图

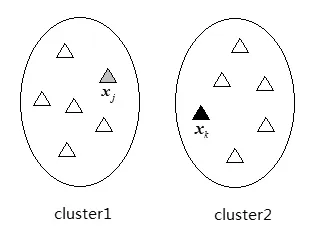
图2 负关联约束关系样本点示意图

定义4 定义样本点对（xj，xk）的交叉熵为

式（2）给出了交叉熵的具体数学表达式，该表达式与信息熵（1）的数学表达式相似。从结构上看，可把信息熵H（xj）看成是样本点xj对其自身的样本交叉熵H（xj，xj），是交叉熵的一种特殊情形。式（2）交叉熵有如下分解

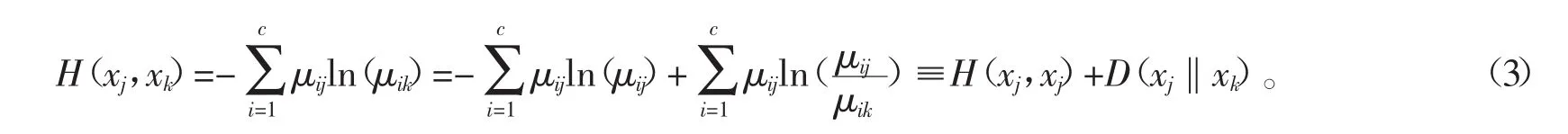
在式（3）中，H（xj，xj）即为信息熵H（xj），表示样本xj的自信息（Self-information），D（xj‖xk）为样本点对（xj，xk）的相对熵（外部信息）。下文中的信息熵，皆用符号H（xj，xj）表示。在CE-sSC算法中，每对成对约束的交叉熵皆可分解成信息熵和相对熵，经分析发现某些熵项之间存在互相干扰，这会使得惩罚项系数的调整复杂化。假设有两对正/负关联约束（xj，xk）和（xj，xk'），其中k≠k'；分解对应的交叉熵得到

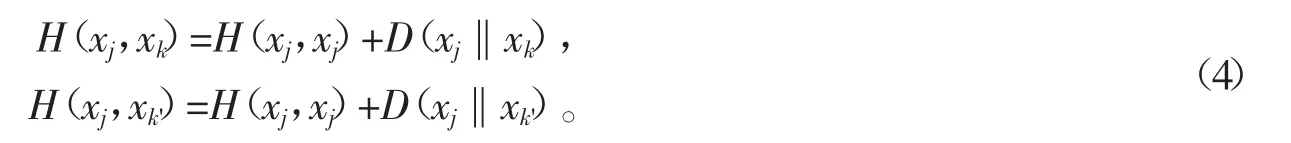
从式（4）可得，两对关联约束（xj，xk）和（xj，xk'）对应的交叉熵H（xj，xk）和H（xj，xk'）中皆包含样本xj的信息熵H（xj，xj）。此时，在CE-sSC算法的惩罚项中，H（xj，xk），H（xj，xk'）和H（xj，xj）三项之间存在相互干扰。正关联约束和负关联约束的惩罚项系数的符号相反，两者之间一旦存在干扰，会使干扰交叉化和复杂化。一般地，成对约束越多，干扰越复杂。

定义2和定义3强调了成对约束样本对的顺序；而在文献［34］中给出的must-link约束类和cannot-link约束类并没有强调顺序；这进一步强化了CE-sSC算法中各熵项之间的互相干扰。鉴于熵项之间的相互干扰，本文将对CE-sSC算法做相应的改进。

贺杨成等［35］研究了成对约束属性对半监督聚类效果所产生的影响；尹学松等［36］通过对正关联约束进行打包，提出基于成对约束的K均值算法（PCBKM），并结合线性判别分析处理高维数据的半监督聚类问题；蒋伟进等［37］提出了一种主动学习更新成对约束的半监督谱聚类算法（SSC）；肖宇等［38］研究了基于近邻传播的半监督聚类算法（SAP）。

相对熵D（xj‖xk）又被称为Kullback-Leibler（KL）散度［39］，可度量两个概率向量之间的距离。概率向量之间相似度越高，对应的KL散度越小。Cressie等［39］将KL散度推广到功效散度（power-divergence，PD），用于研究多项概率模型的拟合优度检验。在数据样本量很大时，基于PD散度的拟合优度检验与基于KL散度的拟合优度检验结果差别不大；但当样本量不大时，差别很明显，模拟实验表明，基于PD散度的拟合优度检验比基于KL散度的拟合优度检验结果更好。

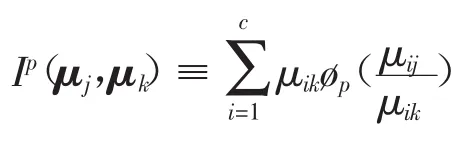
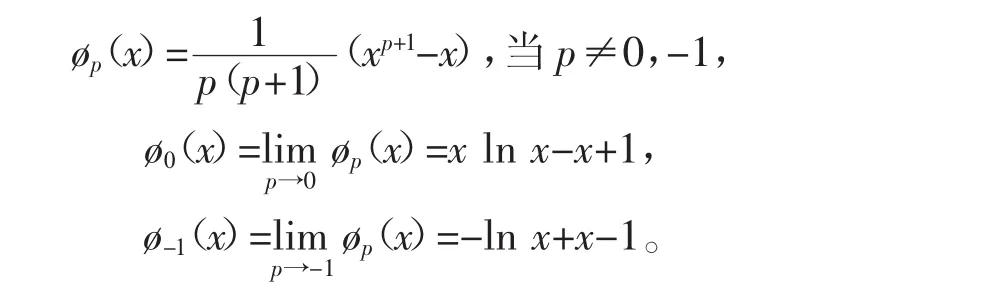
由定义5可知，PD散度是一族，当指标p=0时PD散度也为KL散度，即样本对之间的相对熵。PD散度随着指标p的改变而改变。还可将PD散度推广到更一般的形式，例如ø散度［40］。类似于KL散度，概率向量之间相似度越高，则对应的PD散度越小。基于PD散度和相对熵之间的关系，本文将在下一小节提出一种基于PD散度的半监督聚类算法（Power-divergence Semi-supervised Clustering Based on Pairwise Constraints，PD-sSC）。

1.2 目标函数

由定义1和定义2可知，同一个数据的must-link约束类和cannot-link约束类没有交集，即ML∩CL=Ø。基于集合ML、CL，下面定义惩罚系数矩阵。

定义 6 惩罚系数矩阵 Γ＝（Γjk）n×n，其中

显然，Γ为上三角形矩阵，其中所有γjk元素皆为正数。

CE-sSC算法的惩罚项为

由对式（4）的分析可得，CE-sSC算法的惩罚项Θ0内部之间存在相互干扰，且成对约束越多干扰越复杂。为克服此缺点，我们用PD散度构造如下新的惩罚项

构造如下PD-sSC算法的目标函数

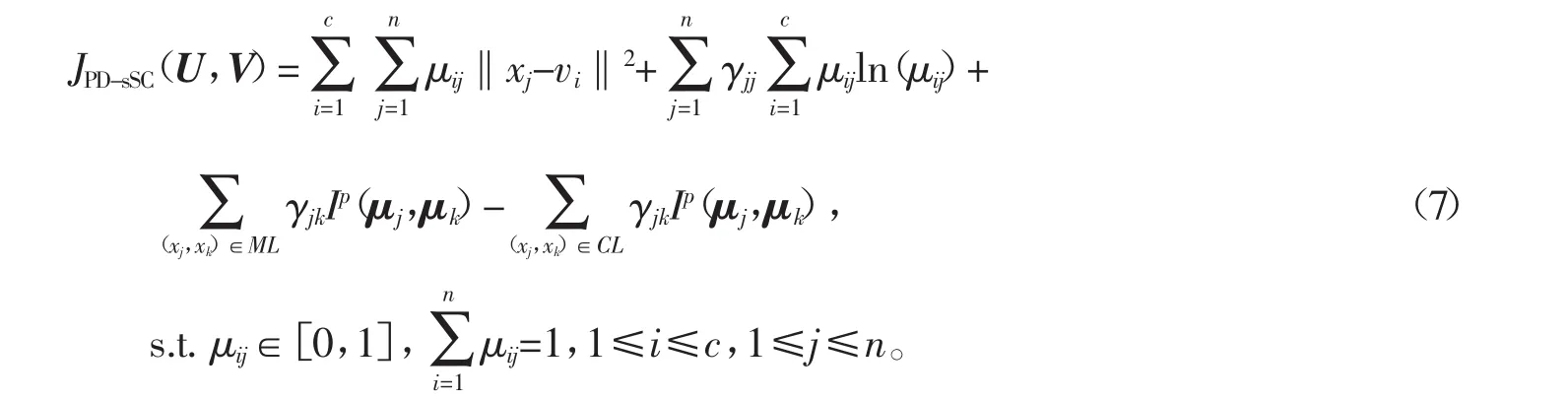
式（7）中的符号含义如表1所示。

表1 PD-sSC算法目标函数符号含义表

1.3 算法步骤

聚类的过程就是最小化目标函数，得出合适的隶属度矩阵和中心矩阵，本文采用极小值。设拉格朗日函数为 L（U，V，Λ），其中 Λ=（λ1，…，λn）T为拉格朗日乘子，则有

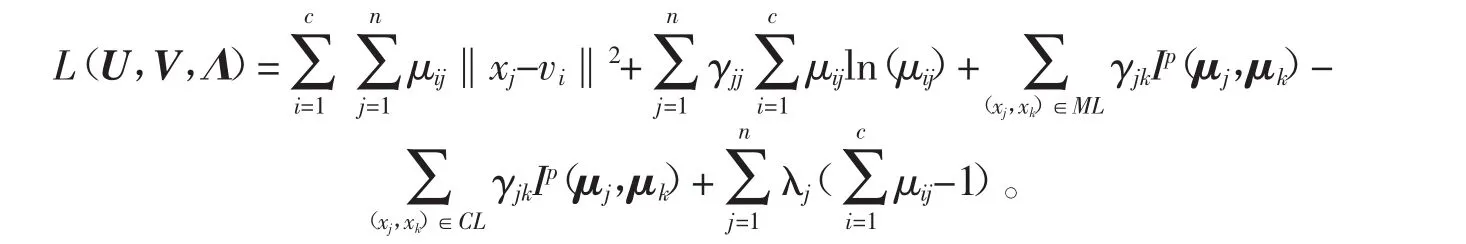
当 L（U，V，Λ）取极小值时，应满足

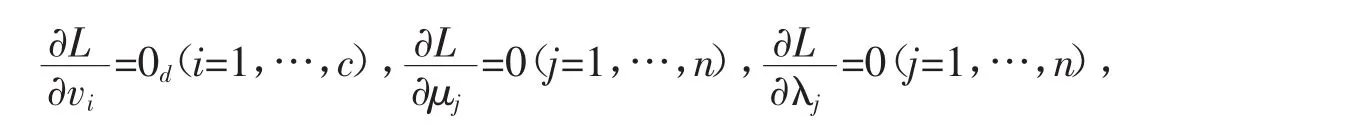
可得

由迭代式（8）和（10），可得PD-sSC算法的流程如下：

输入 数据样本集 X=｛xj│xj∈Rd，j=1，…，n｝，惩罚系数矩阵 Γ＝（Γjk）n×n，初始隶属度矩阵 U(0)，聚类数c（2≤c≤n），PD散度指标p，算法迭代终止条件ε，最大迭代次数T。

输出 隶属度矩阵U和中心矩阵V。

迭代过程：

S1设置迭代计数器t=0。

S2 利用式（8）和 U(t)计算出 V(t)。

S3 利用式（10）和 V(t)更新 U(t)为 U(t+1)。

S4若满足‖U(t)-U(t+1)‖F≤ε或t=T，则终止；否则令t=t+1，并返回S2。此处，‖·‖F表示Frobenius范数。

S5当算法收敛后，输出隶属度矩阵U和中心矩阵V。

聚类中心矩阵与隶属度矩阵的交替迭代更新是PD-sSC算法流程的主要思想。聚类中心矩阵和隶属度矩阵更新迭代计算的时间复杂度分别为

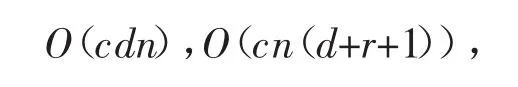
其中，c，n的含义见表1，d为数据样本集X的维数，r表示X中有成对约束关系的数据样本个数。若算法迭代t次，算法的时间复杂度为O（tcdn+tcn（d+r+1））。若仅考虑样本量n，PD-sSC算法的时间复杂度是样本量n线性函数。

2 实验分析

2.1 实验数据与评价准则

选用UCI数据库中常用的iris、wine、seeds、breast数据以及用于池塘水质评价水色图像特征数据集X1和用于区域环境质量状况评价的空气质量数据集X2作为实验数据，特征见表2。表2中breast数据有16个缺失值，在实验过程中将包含缺失值的行做删除处理。实验前，对数据进行中心化与标准化处理，以消除指标的量纲差异。

对比算法选择了 CE-sSC［34］算法、PCBKM［36］算法和 SSC 算法［37］。本文没有考虑文献[34]选中的 SAP算法［38］，是因为SAP算法没有事先固定聚类数c，而是通过偏向系数来自动控制聚类数。实际的数据分析表明，通过调节偏向系数而把最终聚类数恰好控制为c，此过程并不容易实现。

表2 数据集的特征

为了准确评价聚类算法的性能，本文选择了三类常见的聚类评价指标：1）准确率（Accuracy Cluster，AC）指标：描述聚类正确的百分比；2）标准互信息（Normalized Mutual Information，NMI）指标：衡量两个数据分布的吻合程度；3）兰德指数（Rand Index，RI）指标：用来表现聚类结果与真实情况的吻合程度。三类指标取值都在0到1之间，越大说明聚类效果越好。

2.2 实验结果与分析

实验过程中对每个数据集分别固定成对约束数目，其中iris选择的固定成对约束数目依次为10，15，20，25，30，35，40，45，50，55 对；wine 选择的固定成对约束数目依次为 8，16，24，32，40，48，56，64，72，80 对；seeds、X1、X2选择的固定成对约束数目依次为 10，20，30，40，50，60，70，80，90，100 对；breast选择的固定成对约束数目依次为 20，40，60，80，100，120，140，160，180，200 对。对各个数据集中每个固定数目成对约束都进行1 000次的重复实验，每次实验都从数据集中随机抽取相应数目的成对约束，用于指导各算法对数据集的聚类学习。把1 000次重复实验结果的平均值作为该固定数目成对约束的最终实验结果。本文PD-sSC算法的PD指标p选择了区间［-2，2］中的等距格子点，间距为0.05，对应的实验结果有好有坏，罗列出来的是表现较好的PD指标p的实验结果；不同数据的PD指标p 的结果有区别，例如 iris、wine、seeds、breast数据 p=-1，X1数据 p=0.25，X2数据 p=-1.75；实验结果表明，在实际的数据分析中，通过调整PD指标p来选择PD-sSC算法具有一定的意义。算法迭代终止条件为ε=le-5，最大迭代次数T=100。

图3～10分别为6个数据集的3个指标值实验结果。其中，横坐标为成对约束数目，纵坐标分别为AC指标的值、NMI指标的值、RI指标的值。

图3显示当成对约束数目不大于45时，PD-sSC算法的AC与RI指标值高于3个对比算法，NMI指标值比CE-sSC和PCBKM高。PD-sSC和CE-sSC算法的3个指标值都在缓慢下降；在约束数目为50时，PD-sSC和CE-sSC的指标值下降较为明显。虽然SSC算法的NMI值远超PD-sSC算法和CE-sSC算法，但SSC算法中含有两个对算法效果影响很大的超参数，计算速度相较其他三种算法十分缓慢，SSC算法复杂度高。

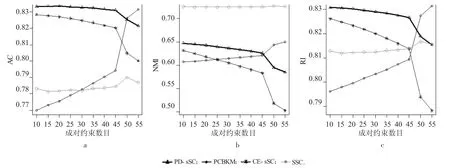
图3 iris数据集实验结果

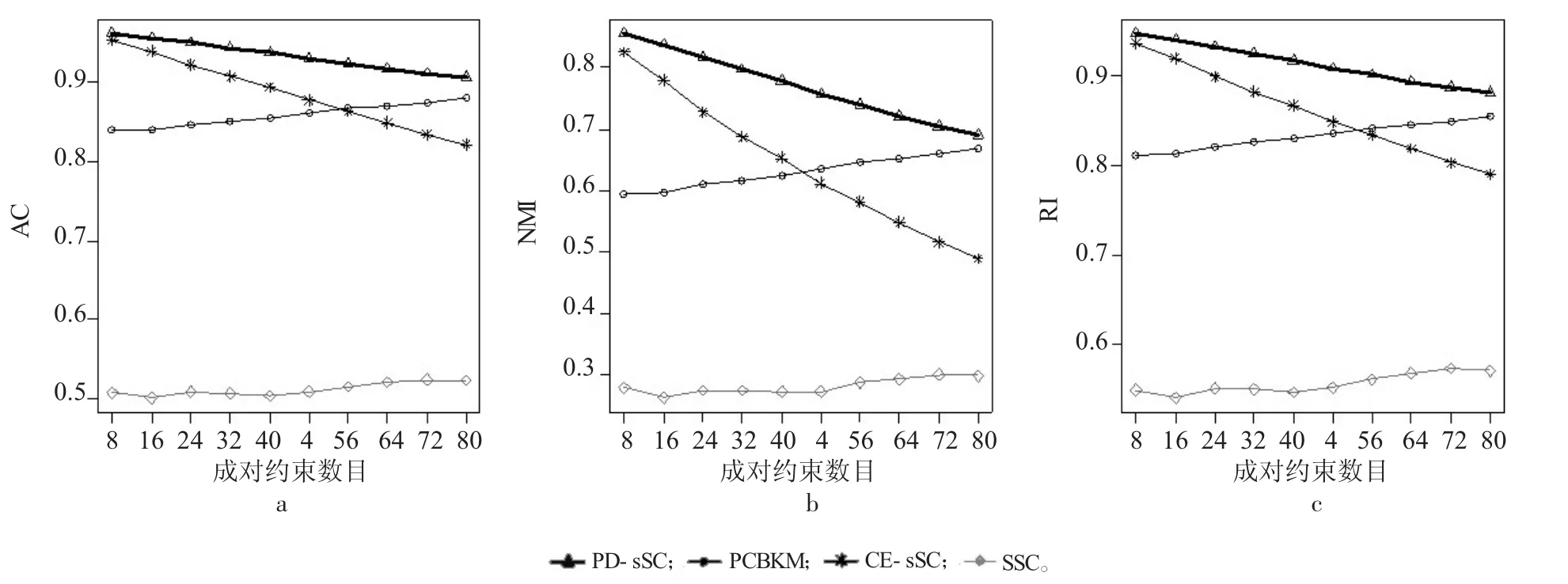
图4 wine数据集实验结果

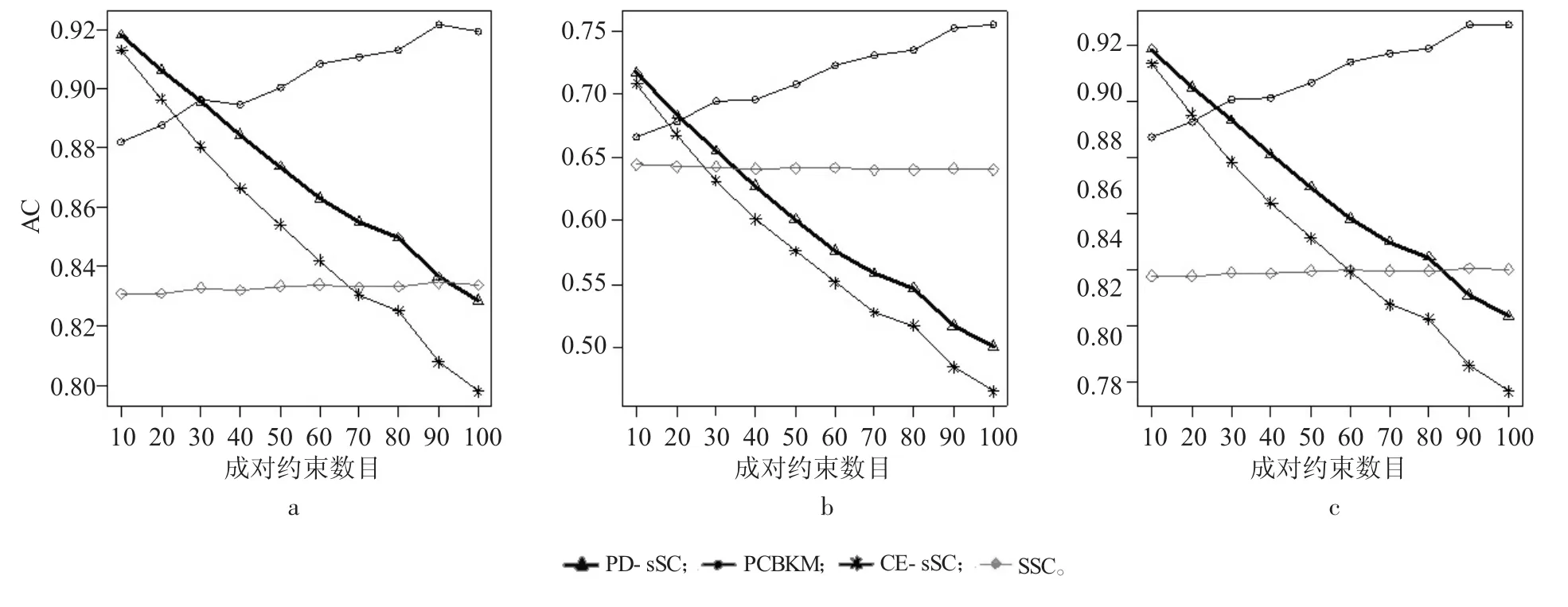
图5 seeds 数据集实验结果

图4中wine数据集实验结果表明，PD-sSC算法的AC、NMI和RI指标值都明显高于其他3个算法，PD-sSC算法和CE-sSC算法曲线都呈下降趋势，且AC和RI指标值都高于0.85。PD-sSC算法的聚类效果最好。

在图5中，PD-sSC算法成对约束数目小于20时，3个指标值比对比算法高。PD-sSC算法聚类效果优于CE-sSC算法，且AC和RI指标值都高于0.80。随着成对约束数目的增加，PD-sSC算法和CE-sSC算法聚类效果随之下降，但PD-sSC算法的下降速度稍缓于CE-sSC算法的下降速度。

图6 breast数据集实验结果

图7 X1数据集实验结果

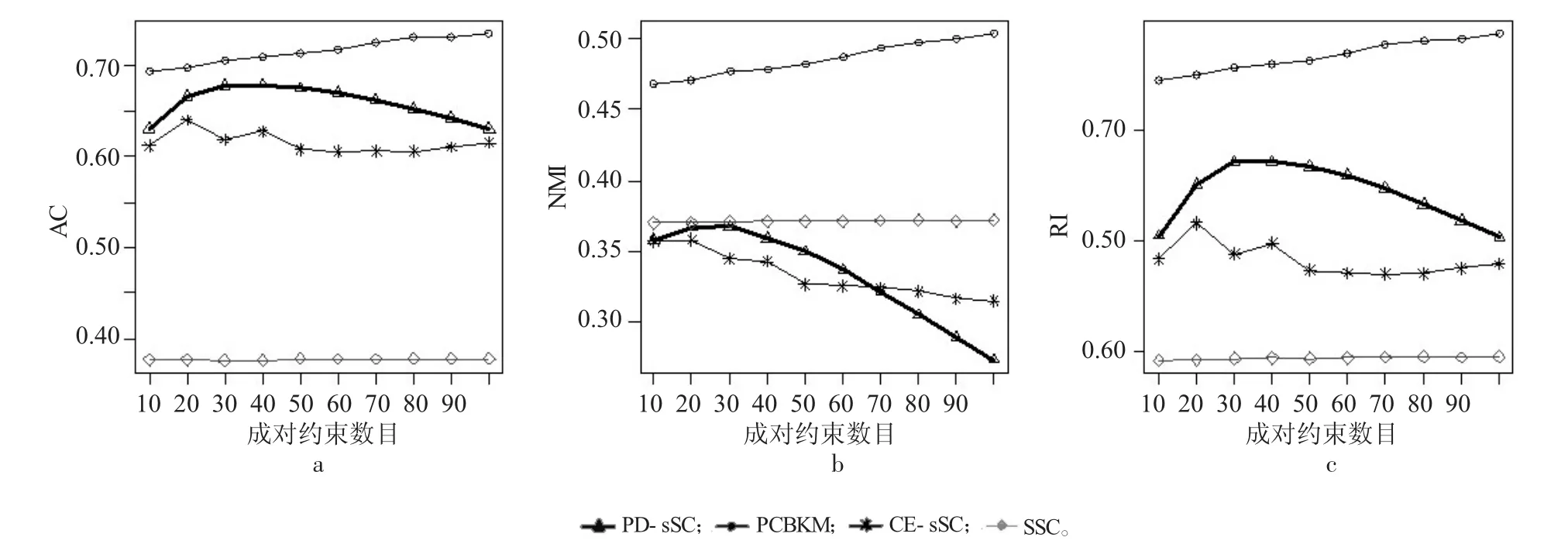
图8 X2数据集实验结果

图6表明PD-sSC算法对breast数据集聚类效果最好。由于breast数据集样本量相对较大，SSC算法速度极慢，因此在计算时没有考虑SSC算法中主动学习部分，只考虑了半监督谱聚类算法。随着成对约束数目的增加，除SSC算法的指标值基本固定不变外，其他3个算法的指标都有下降趋势，其中PCBKM算法降幅最大，PD-sSC算法降幅最小，且AC和RI值都大于0.85。

由图7可知，当成对约束数目小于30时，PD-sSC算法与CE-sSC算法的AC、NMI和RI指标值相差不大，但明显优于其他两个算法。随着成对约束数目的增多，PD-sSC算法的AC和NMI指标值高于CE-sSC算法，当成对约束数目大于80时，PD-sSC算法的RI指标值略高于CE-sSC算法。从整体看，PD-sSC算法的AC、NMI指标值是波动上升的，且聚类效果优于其他三个算法。图8给出的X2数据集实验结果表明，PCBKM算法的聚类效果最好，PD-sSC算法的AC指标值与RI指标值一直高于CE-sSC算法。

一般而言，成对约束数量越多，聚类效果应该会越好，但根据上述分析，PD-sSC算法和CE-sSC算法的聚类效果都随着成对约束数目的增多呈下降趋势。此现象的可能原因是，为简化实验过程，选择了固定的惩罚系数，当成对约束数目增加时，目标函数JPD-sSC（U，V）中的惩罚项比重会增加，从而影响了聚类效果。此时，可选择随成对约束数目增加而减小的惩罚项系数，降低惩罚项的比重，以期获得更好的聚类效果。以iris、wine数据集为例，随着成对约束数目的增加，适当减小惩罚系数的值，对CE-sSC算法惩罚系数分别取为（10/N）3，（10/N）4.5，对 PD-sSC 算法惩罚项系数分别取为（10/N）4，（10/N）5.5，其中 N为成对约束数目。

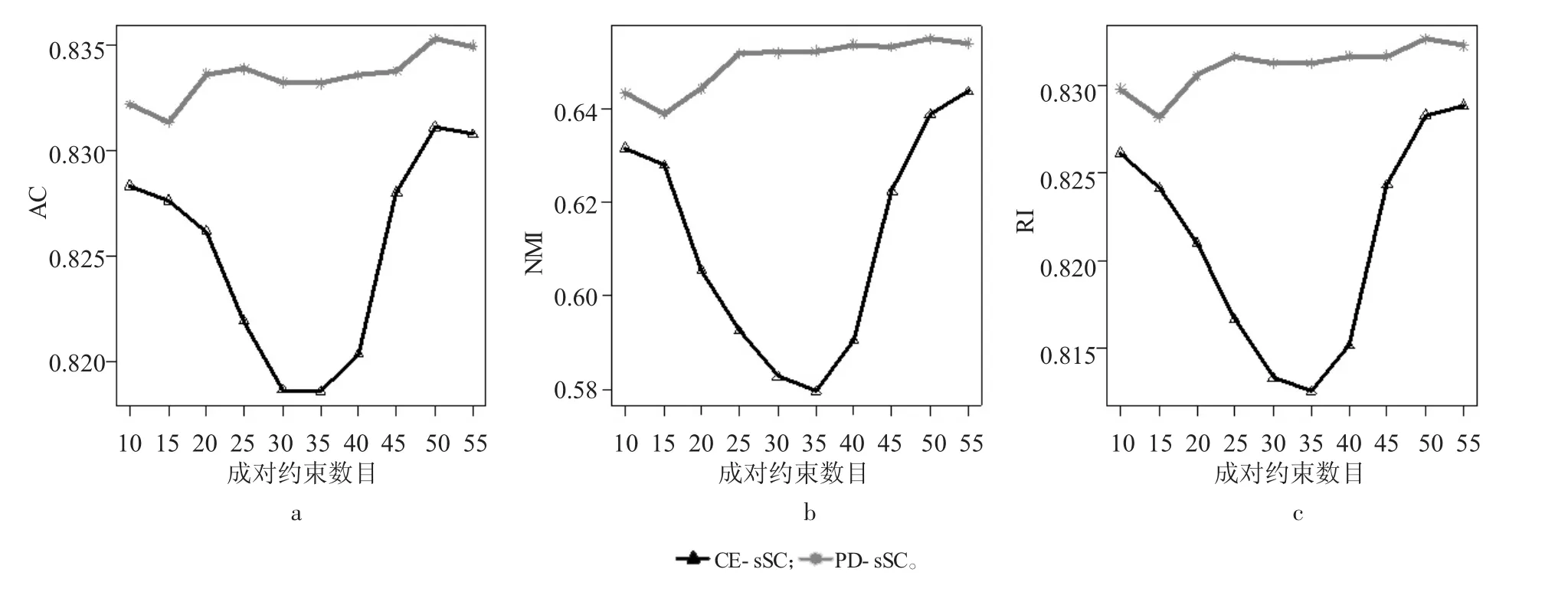
图9 iris数据集调整惩罚项系数后实验结果

图10 wine数据集调整惩罚项系数后实验结果

由图9～10可知，惩罚系数被调整以后，PD-sSC算法的3个指标值都有波动上升趋势，聚类效果有明显提升。在图9中，当成对约束数目为大于35时，CE-sSC算法指标值持续上升；PD-sSC算法的指标值在成对约束数目大于15时小幅波动上升。在图10中，CE-sSC算法在成对约束数目为20～80时指标值都持续下降，而后小幅上升，成对约束数目取100时，3个指标值都比成对约束数目取10时低；PD-sSC算法的指标值在成对约束数目为20时达到最高，但总体呈小幅上升之势。试验中对CE-sSC算法的惩罚系数进行调整比PD-sSC算法难，因为CE-sSC算法的惩罚项内部之间互相干扰，影响了惩罚系数的调整效果，这也是本文引进PD-sSC算法的原因之一。

综合图3～10的实验结果得出，对成对约束数目较少的数据集，PD-sSC算法的聚类效果优于其他对比聚类算法。生活中获取带成对约束的数据比较困难，因此本文所提出的算法是有意义的。PCBKM算法是利用Must-link约束对数据进行打包，然后再进行聚类分析，因此可预计，在成对约束数目较大时，该算法的聚类效果可能会很理想，图3～5以及图8证实了这种猜想。

表3列出了各算法计算时间的复杂度。可看出，SSC算法的时间复杂度为立方阶，相较其他3个算法，在实际运用时耗费的时间成本更高。虽然在PD-sSC算法中式（11）形式上较复杂，但程序实现并不复杂；PD-sSC算法和CE-sSC算法具有相同的时间复杂度，这在实验过程中就有体现。

表3 各聚类算法的时间复杂度

3 结语

为克服CE-sSC算法的惩罚项中各熵项之间的相互干扰，本文基于相对熵提出了PD-sSC算法，并把表示成对约束样本信息（外部信息）的KL散度（即相对熵）项推广到了PD散度。PD指标p可取任意的实数，当成对约束数较少时，可通过调整PD指标来选择比CE-sSC算法表现更好的PD-sSC算法。选择了CE-sSC算法、PCBKM算法和SSC算法作为对比算法，PD指标选择了区间［-2，2］中的等距格子点进行比较，挑选了表现较好的PD指标进行展示，不同数据的PD指标有可能不同。实验结果表明，在成对约束数目较少时，PD-sSC算法聚类效果比对比算法更好，在处理样本量较大的数据集（例如breast）时，PD-sSC算法明显优于其他对比算法。如果设定惩罚系数随成对约束数目的增多而减小，此时PD-sSC算法聚类效果会得到进一步提升。PD-sSC算法的惩罚系数调整比CE-sSC算法简单且高效。在分析iris、wine和seeds数据时，当成对约束数目相对较大时，PCBKM算法表现较好，这与该算法直接对must-link成对约束样本进行打包处理有关。未来的研究，将参照PCBKM算法的这个特点，对PD-sSC算法做进一步的优化处理。