一种利用级联小波变换的ICESat-GLAS波形去噪方法

谭建伟，王志勇,2，徐志达

(1.山东科技大学 测绘科学与工程学院，山东 青岛 266590；2.测绘工程国家级实验教学示范中心(山东科技大学)，山东 青岛 266590)

ICESat即冰、云和陆地高程卫星，是全球首个星载大光斑激光雷达测高卫星，搭载着地球科学激光测高系统(GLAS)[1]。由于其穿透能力强的特性，能高精度的获得地表物的垂直结构信息。大光斑激光雷达系统已被证明可准确估计森林结构特征[2]，如林区冠高、郁闭度和生物量等。但激光脉冲在大气层的传播过程中会产生折射、散射和延迟，加上系统本身的噪声影响，使得接收的波形存在大量的白噪声；另外当GLAS激光脚点照射在地形陡变处和枯草处等地物时，其回波信号可能会出现失真，波形信息叠加等情况[3]，为获得可靠性高的反演结果，需探寻一种去噪性能良好的波形去噪方法。

S.Mallat[4]提出用于多分辨率小波分析的Mallat算法来对原始含噪信号进行快速小波分解和重构，该算法能够避免信息采样密集度随尺度值大小变化的缺陷。DonohoD L[5]于1995年初次阐述了小波软阈值去噪的观念，并对“去噪”这一术语作出正式的解释，通过优化均方根误差来达到平滑信号的效果。邱赛[6]等人将小波去噪的方法应用到ICESat-GLAS波形数据处理中，通过对各小波基参数特性的分析比较，认为sym7小波基函数更适用于ICESat-GLAS波形去噪。谢加华[7]等人采用级联离散小波变换进行信号去噪，在同样的分解层次下，将分解的低频部分中的高频细节信号进行再分解，其去噪效果强于传统的小波噪声阈值法。在结果精度评价方法方面，朱建军[8]等人研究对比现有的均方根误差、信噪比、互相关系数、平滑度和综合评价法等小波去噪质量评价指标，发现前两种评价指标应用较为广泛且一般能获得较为可靠的评估结果，后三种质量评估指标的性能受数据条件的约束以至于可信度较低。为解决阈值选取难以及传统小波阈值法去噪效果不佳等问题，本文在上述学者提出的去噪方法基础上，采用自适应阈值的级联离散小波变换方法来对ICESat-GLAS波形进行去噪处理，并通过均方根误差和信噪比来评价其去噪性能。

1 ICESat-GLAS研究数据

ICESat是美国航空航天局(NASA)于2003-01-12发射到590 km高度的圆形极地轨道的空间激光雷达卫星[9]。GLAS数据产品包括15种标准数据产品以及一些辅助数据，分别为GLA01～GLA15。其中GLA01为全球测高的全波形数据产品，包括激光印点的位置、脉冲强度及接收时间等信息，1 s内的40个激光脚点共享一个地理坐标，每个激光足印在地表形成的直径约为72 m，相邻足印中心间距170 m[10]。记录回波样本中，以时间为序列，陆地记录544帧数据，对应地表81.5 m的测高范围；幅值代表波形脉冲的振幅大小。

本文采用的是美国冰雪数据中心(NSIDC)自2017年8月起推行的HDF5格式的GLA01数据，由于地物类型和脉冲包络形状(高斯峰的数量及其宽度)存在明确的依赖性[11]，为获得直观地去噪效果，选取2009-10-09的陆地平坦地区的地物回波信号，为level 1A级产品，利用MATLAB平台结合GLAS数据字典，可对原始波形信息进行读取，并将其幅值强度压缩至[0,255]，其波形信息如图1所示。

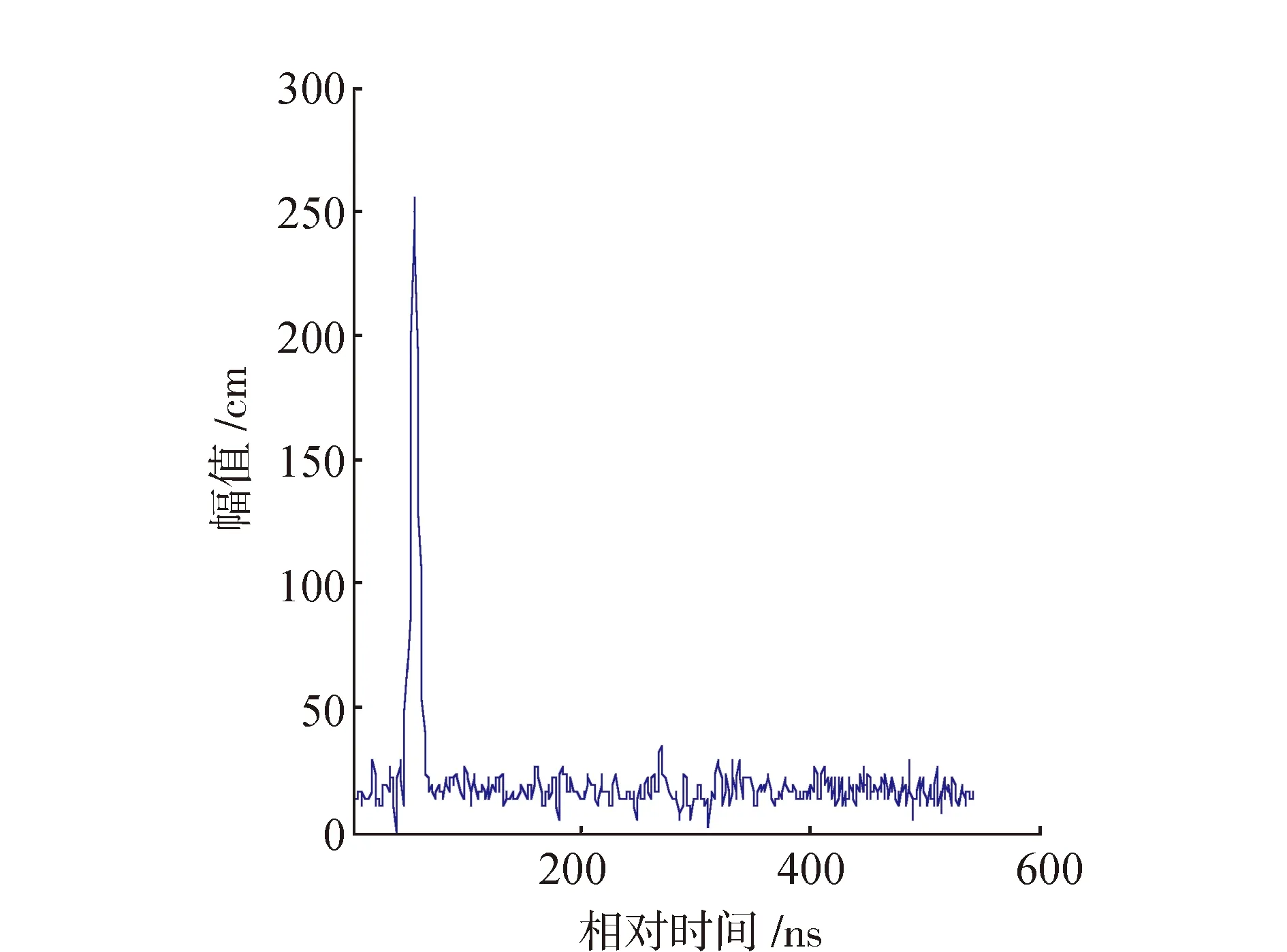
图1 GLA01原始含噪波形图

2 级联离散小波去噪原理

2.1 离散小波变换

(1)

2.2 级联离散小波变换

在小波分解中，大尺度因子分解系数用来代表信号的近似部分，小尺度因子分解系数则用来代表信号的细节部分。根据Mallat快速算法[4]，原始信号f(t)在分辨率为2-j+1下的近似部分可继续分解为分辨率2-j下的近似部分Cj和细节部分Dj之和[7]，即

(2)

其中，j为分解层数，k为采样点，φ(t)为尺度函数，Cj和Dj分别是由Cj-1与尺度函数的低、高通滤波器进行卷积运算而得。二者之间的系数关系：

(3)

(4)

式中：n为采样点数，cj,k,dj,k代表第j层小波分解得到的近似和细节部分系数；g0(n-2k)和h0(n-2k)分别为高、低通滤波系数。

根据式(2)将所提取的近似分量作一层小波分解，并将提取出的低、高频分量分别进行三层小波分解，同时将第一层分解获取的细节分量进行四层小波分解，最后对这3种路径获取的低、高频信号进行去噪处理，按照小波系数分解的逆过程可实现信号重构过程，获得去噪后的信号[7]。其具体流程如图2所示。

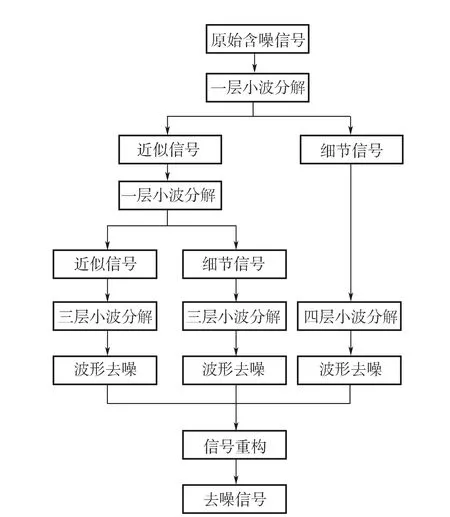
图2 级联小波变换去噪流程图

2.3 信号去噪

1)小波基选择。小波基函数的选择需参考不同的实验要求以及应用目的，即使对同一波形数据使用不同的小波基函数进行处理的结果也各不相同，所以选用合适的小波基函数对波形去噪尤为重要。Symlet小波系不仅包含Daubechies小波系的所有优良特点，同时为减少信号失真等情况，在对称性能进行改进。邱赛[6]等人通过分析各小波基函数数学特征(正交性、紧支性、对称性、正则性、消失矩)以及实验发现，sym7比db1、db6和sym4等小波基函数更适用于GLAS回波信号的去噪。

2)信号去噪。小波分析应用主要是进行信号去噪[13]，采集到的信号都具有一定的噪声且大多数都是高斯白噪声。根据Stein的无偏风险估计原理[14]可知，将选取的各阈值计算其风险并绘制风险曲线图，风险值最低处所对应的小波变换系数可被认为是最优解，从而达到自适应阈值选取的目的，下一级尺度的阈值选择由上一级尺度系数的噪声水平来决定，有效避免在每个级别尺度使用相同阈值的缺点，在软阈值函数条件下，所得到的阈值趋近于理想阈值[15]。其基本原理为

将原始信号y(i)中的N个分辨级元素的绝对值依次取平方，再按升序排列以获得新的信号向量序列f(i)，即

f(i)=(sort(|y(i)|))2,(i=0,1,…,N-1).

(5)

若取f(i)的第k个元素的平方根作为阈值λk，即

(6)

则该阈值产生的风险为

(7)

利用各风险值R(k)绘制风险曲线，其风险曲线最低处所对应的元素为kmin，根据式(6)可得阈值：

(8)

利用算法计算得到阈值后，需构建阈值函数来去除含有噪声因子的小波系数。软、硬阈值函数是目前应用较为普遍的阈值函数[16]，硬阈值函数注重于均方误差的大小，高于设定阈值的系数保持不变，反之则置为0，适用于对独立数值的优化问题求解，但其不连续性会产生阶跃现象，为防止出现过度平滑现象，本文采用软阈值函数对阈值进行处理，当小波系数ω的绝对值低于给定的阈值λ，将它设置为0；反之，则按某一固定量收缩[16]，即用ω减去λ，并通过符号函数sgn()来控制正负性，即

(9)

3 实验结果及分析评价

通过实验对比研究自适应阈值级联去噪法和3种传统的小波去噪方法在ICESat-GLAS波形去噪中的性能，为更好评价4种方法的优劣性，实验中均采用相同的sym7小波基函数进行5层小波分解。以激光点号1的波形为例，传统的噪声阈值法是通过获取噪声的方差来确定阈值，从而达到精确降噪的目的；噪声阈值级联法是通过噪声阈值法结合合级联小波变换的思想来实现去噪作用；自适应阈值法是采用SURE(Stein’s Unbiased Risk Estimation)准则[14]，即Stein的无偏风险估计原理确定阈值，进而达到降噪目的；本文采用自适应阈值级联去噪法则是在自适应阈值选取算法的基础上，对原始含噪信号的高频细节部分进行再分解，从而获得更为精确的去噪信号。四种方法的去噪效果分别如图3—图6所示。

图3 噪声阈值法

图5 自适应阈值法

图6 本文方法

在波形去噪性能评估体系中，常用的客观评价指标分别为均方根误差(RMSE)和信噪比(SNR)，其内涵都是通过比较处理前后信号的差异来衡量去噪的性能。RMSE是描述处理前后波形信号之间的均方误差，其值越小代表去噪的效果越理想。SNR是描述信号有效成分与噪声成分的比例关系参数，一般认为，SNR越大，去噪的效果越好[17]。其具体式分别为：

(10)

(11)

式中：y(i)和q(i)分别代表去噪前后信号，L代表信号的长度。

据表1可知，采用噪声阈值法对ICESat-GLAS波形数据进行去噪，其信噪比为20.625，均方根误差为2.840；采用噪声阈值级联法去噪的信噪比为25.028，均方根误差为1.739；自适应阈值的信噪比28.336,均方根误差为1.185。3种方法在一定程度上都达到波形去噪的目的，使去噪后波形都比原始波形更加平滑，但从图3—图6以及表1的误差对比结果来看，去噪效果都不理想，存在过度平滑、波峰前后噪声没有得到有效去除等问题。造成问题的主要原因：其一，阈值选取算法的不合理，根据整体波形的噪声水平来设置阈值，没有考虑波形前后元素间的相关性和部分高频细节信号也是有用信号以至于产生“一刀切”等过度平滑现象；其二，在小波系数分解过程中，没有将低频部分信号中的高频含噪信号进行进一步消除，以至于去噪效果不理想。

本文采用自适应阈值的级联小波变换来对GLAS回波信号进行去噪，在一定程度上克服了上述问题，使高频噪声信号得到有效去除，保留部分细节有用信号，避免过度平滑等问题。由表1可知，自适应阈值级联去噪法的信噪比为29.211，均方根误差为1.075，均优于前三种方法，可见该方法的去噪性能较传统的小波噪声阈值法而言，有着一定改进作用。

表1 4种方法去噪信噪比和均方根误差的比较

4 结 论

在ICESat-GLAS回波信号的预处理中，波形去噪的结果好坏关系着后续的波形分解以及特征参数的提取等步骤，进而影响GLAS回波信号在林区树高、生物量以及数字高程模型(DEM)提取等的精度。本文在分析传统小波变换去噪的基本原理和现有阈值选取算法的基础上，构建一种自适应阈值的级联离散小波变换进行ICESat-GLAS回波波形去噪的方法，该方法通过无偏风险估计原理自适应确定阈值结合级联离散小波变换的思想对ICESat-GLAS原始回波信号进行去噪处理。经实验结果对比表明，在ICESat-GLAS大光斑激光雷达波形数据去噪处理方面，自适应阈值级联去噪方法要优于传统的噪声阈值去噪和自适应阈值去噪等方法。

由于本文采取的实验样本有限，不排除偶然误差出现的可能。在今后的研究中，将增加实验样本数量，并将对阈值函数的选取进行进一步探讨，比如采用半阈值函数等，同时对不同位置和地形特征的波形信息进行处理比较以提高实验结果的可靠性。