基于卫星测高数据的萨德湿地水位变化研究

井发明，陈海珍，包 颖，李 璐

(宁波市测绘设计研究院，浙江 宁波 315042)

卫星测高是利用人造地球卫星携带的测高仪，测定卫星到瞬时海平面(或平坦地面)的垂直距离的主动式雷达遥感技术，具有覆盖范围大、重返周期短、精度较高等特点。最初目的是为测量全球海平面变化，随着技术的发展，卫星测高在反演陆地水域水面高度的应用潜力慢慢被挖掘。卫星测高在内陆水域的研究主要集中在大型河流湖泊，以及大型湿地的恒定水域范围，Brooks在80年代初就尝试用SeaSat卫星数据测量大型湖泊水位；Cheney在1988年使用Geosat数据绘制1986—1987年的厄尔尼诺现象[1]；但由于精度不高，数据时间周期短，早期的卫星测高应用有限。随着卫星测高技术的发展，测高精度不断提高，数据时间序列增长，90年代以来，国内外学者不断探索卫星测高在气候敏感型大型湖泊和大型内陆水域的应用，尤其是水位变化、水体范围变化与气候变化之间的关联。Siegert等对南极冰湖的变化进行了系列研究[2-5]；A.R. Harris等对全球几大湖区的水位变化和水体范围变化进行了监测和分析[3]；随着Topex/Poseidon(TP)卫星的发射，遥感测高精度得到进一步提高，其应用也更加广泛。Morris对北美的五大湖的水位变化进行了误差精度4 cm以内的分析[4]；Singh等学者利用卫星测高技术很好的展示了咸海的萎缩和消亡的历史变迁[5]；Zakharova等人还将卫星测高应用于亚马逊流域[6]；全球超过100个大型河流湖泊使用卫星测高技术进行水位和水域监测。目前已有少数利用卫星测高技术反演湿地及湿地的洪泛平原水位变化的研究[7]，但总体而言，在湿地的应用还很有限。

1 研究区域简介

萨德湿地位于非洲东北部南苏丹(如图1所示)，为世界上最大的湿地之一，萨德湿地的面积随着季节的变换而变化，占地面积平均为3万km2，而到了雨季最大可达到13万km2[8]。萨德湿地的恒定水域及其洪泛区给野生动植物提供了重要的生息场所，也是当地民众的谋生之地，萨德湿地(Sudd)已经被列入《拉姆萨尔公约国际重要湿地名录》。但由于其占地范围大，地理环境复杂，政治环境不稳定，给湿地研究带来了巨大的困难。

图1 萨德湿地地理位置

2 数据与方法

2.1 卫星测高数据

本文使用ENVISAT 和Jason-2卫星测高数据。ENVISAT卫星重返周期为30 d；Jason-2卫星重返周期为10 d。数据从OpenADB网站免费下载(http://openadb.dgfi.tum.de/).使用萨德湿地的范围进行查找(经度范围：29°—33°W，纬度范围：5°—10.5°N)，ENVISAT数据为006-094周期(2002年5月至2010年11月)期间，航迹线#0027、#0113、#0199、#0242、#0328、#0485、#0571、#0657、#0786、#0872和#0943。Jason-2数据为001-184周期(2008年8月至2015年4月)期间，航迹线#057、#120、#133和#196,见图2。

图2 ENVISAT(实线)和Jason-2(虚线)航迹(背景图引自Mohamed[17])

2.2 验证数据

本文用于精度检验的实测数据来自Petersen 博士的南苏丹道路和堤坝重建项目[9]，该项目收集了从2004—2006年共计15个实测站点的数据，站点沿着主要水道分布，每小时或每天采集一次。

2.3 卫星测高原理

卫星测高利用测高仪发射已知功率的雷达光束，并接收反射回来的光束，计算其时间间隔，结合卫星轨道高度、仪器校正、环境校正和大地水准面等来推算水面高度及其他相关信息。

水位高度:

WL=Orbital_altitude-Range+RCorrection.

(1)

其中Oribital_altitude为卫星轨道高度；Range为回波重定后的测距。

误差校正:

RCorrection=ΔRDry+ΔRwet+ΔRIonos+ΔRPtides+

ΔRSEtides+ΔRREO.

(2)

其中：ΔRDry+ΔRwet为大气校正；ΔRIonos为电离层校正；ΔRPtides为潮汐导致的垂直扰动；ΔRSEtides为由于太阳运动导致的垂直扰动；ΔRREO为多卫星数据融合时的校正。

2.4 方法流程

水位推算主要包括数据预处理、回波重定、高度计算和数据后处理几方面：①根据轨迹号下载相应的回波数据和各类参数数据；②针对数据进行研究区数据选定，根据数据中的辅助参数(卫星运行状况参数、测高仪角度参数、环境参数等)进行不稳定测量值的剔除，再根据测量值的直方图分布，将明显不合理的测量值剔除；③运用改进的阈值法进行回波重定，得到回波重定后的测距；④将重定的测距代入式(1)和式(2)进行计算得到初步的水位高度测量值；⑤将测量值划分到合适大小的网格中，对每个网格中的测量值进行奇异值剔除，将两组卫星数据进行融合，对长时间序列观测值进行平滑处理；最终得到时间序列的水位高度,具体流程见图3。

2.4.1 回波重定

由于陆地上的地表覆盖情况复杂，测高仪反射回的光束干扰众多，回波形式多样(见图4)，所以必须使用回波重定算法进行距离的重定，才能计算水位高度。

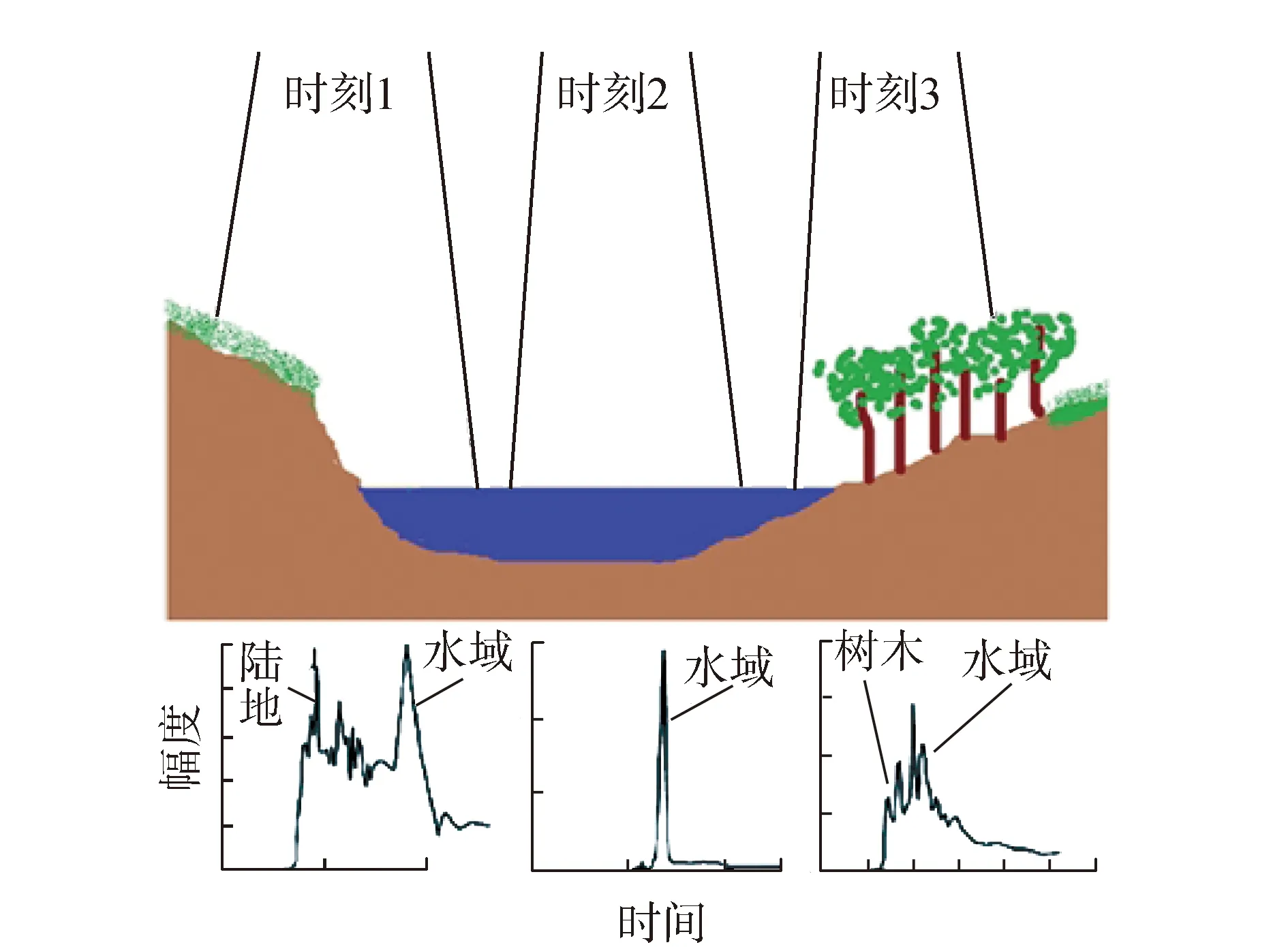
图4 陆地上的3种回波形式(改绘自Maillard[10])

国内外学者提出多种回波重定算法，包括：拟合算法、OCOG算法、ICE-1算法、ICE-2算法、阈值法、改进的阈值法等等；其中，拟合算法不适合内陆水域，OCOG算法在内陆水域中的应用具有不稳定、不收敛的缺点，ICE算法虽适用于内陆水域，但对冰盖回波最优。

本文通过OCOG算法、阈值法、改进阈值法的对比发现，改进阈值法的效果最佳。改进阈值法[11]是在阈值法的基础上，通过对回波的起始噪音部分的剔除，大大减少由于仪器设备等偶然误差导致的观测值误差。本文在研究区范围内随机选取5个试验网格，选取5%、10%、15%、20%和25%阈值分别进行试验对比发现，10%阈值法进行回波重定效果最佳，故本文使用阈值为10%改进的阈值法进行回波重定来推断水位高度。

2.4.2 研究区域网格化

为确保雷达遥感的覆盖范围以及足够的观测值，需对研究区划分网格，默认网格中水位一致，本文测试了0.1°×0.1°，0.2°×0.2°，0.25°×0.25°，0.5°×0.5°，1°×1°等5种网格划分，权衡其覆盖研究区范围及网格内观测值数量(至少20个观测值)，最终选取0.25°×0.25°(约700 km2)的网格(见图5)进行数据的划分。数据并未全部覆盖湿地全区，图中白色区域有观测数据，黑色区域无观测数据。

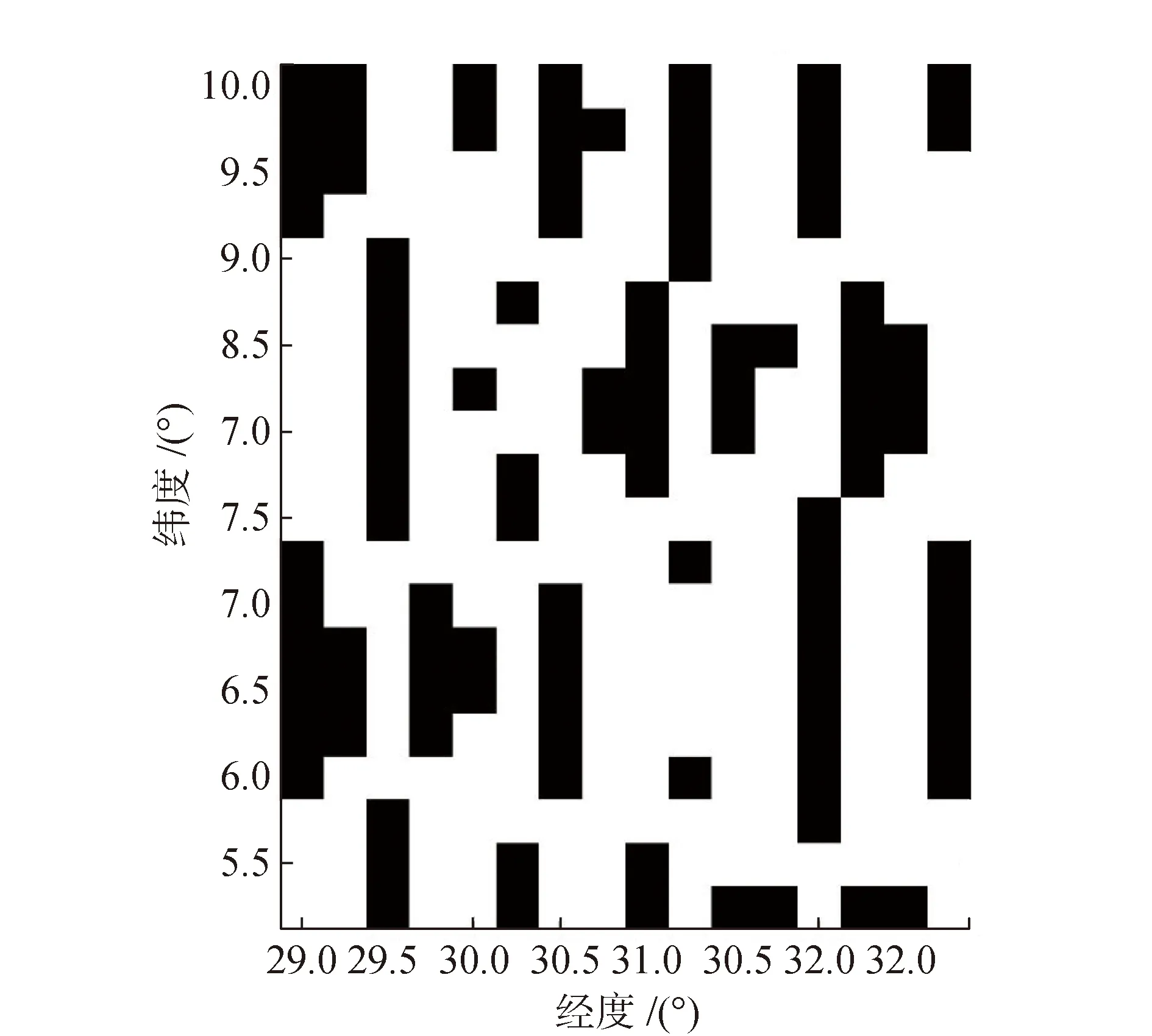
图5 观测值覆盖范围

2.4.3 奇异值剔除与平滑算法

在进行计算之前，首先需要进行数据奇异值的剔除，剔除主要包括4步:①在数据筛选时，应将不准确的测量值去除，包括轨道机动(orbital maneuver)期间的测量值、角度过大时的测量值、雨雪天气的测量值等；②由于萨德湿地旱雨季变化显著，且范围大，水位变化幅度可能较大，数据预处理时，样本数据量大，本文首先选用3δ法则(与临近测量值相差超过3倍标准差的值为小概率事件)，进行全部观测数据的奇异值剔除，剔除约2%观测数据飞点；③在计算网格中水位高度时，网格中的观测值也可能存在奇异值，由于网格中的观测值数量从20至上百个不等，由于样本量较少，故本文测试了狄克逊准则法(Dixon)、格拉布斯准则法(Grubbs)和3δ法则，由于奇异值不止一个，且多分布于同一侧，狄克逊准则法和格拉布斯准则法效果不佳，本文采用3δ法则进行剔除；④每个网格中的水位变化时间序列中也存在奇异值，此时样本数据量适中(ENVI约为100个水位点，Jason-2约为300个水位点)且奇异值很少，本文采用格拉布斯准则法(Grubbs)并对每个剔除结果进行检查核实。

由于重返周期较长，数据为稀疏的点，本文使用局部回归算法(加权线性最小二乘算法)进行平滑和内插，提取趋势线。

2.5 精度检验

由于ENVISAT的重返周期为35 d，工作时间较短的站点实测数据无法使用，工作时间超过10个月的仅有3个实测站点可供对比，本文采用此3个站点水位数据进行精度验证。鉴于卫星测高数据与实测数据的时间重合点仅为2004—2006年期间的部分月份，理论上为同精度测量值，故选用与实测站点最为接近的网格中的水位进行检验，作为整个数据的精度检验结果。实测数据采用的大地水准面与卫星遥感测高数据所使用的不一致，故水位高度不能直接进行对比，常用的指标(如RMSE)不可用，只能对比其变化趋势的相关性。本文使用线性相关系数R(linear correlation coefficient)与光谱角SAM(Spectral angle mapper)作为相关性指标。

由于实测数据的稀缺，测高数据精度检验成为一大难点，卫星测高轨迹交点也是数据精度检验的可靠选择。有两种方式使用卫星测高数据进行精度验证：其一是使用单一卫星数据，将其轨道相交点的数据进行对比，选择最邻近时间点的轨道相交点数据，查看其时间序列，若水位变化趋势相同，略有偏移，则说明测量数据可靠；其二是使用两颗卫星轨道相交点数据进行对比验证。本研究区域中ENVISAT 和Jason-2卫星交点处为滩涂区域，不存在开阔水域，故仅使用ENVISAT 单一卫星数据轨道相交点的测量数据进行精度检验。

3 结果与讨论

3.1 精度检验结果

Shambe水文站点实测数据精度与卫星测高数据对比如图6所示，线性相关系数R为0.968 3，光谱角SAM= 0.000 193。两组数据的高度相关性表明卫星测高数据精度较高。

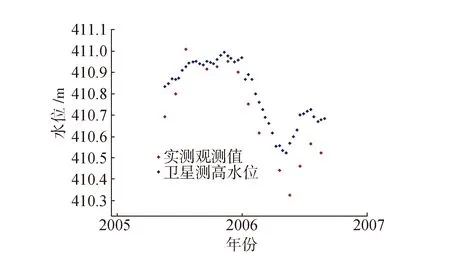
图6 Shambe 水文站点实测数据精度与卫星测高数据对比图

ENVISAT#571和#786轨迹推算的水位时间序列如图7所示，两个轨迹时间间隔为10 d，可以看出，两个轨迹的观测值非常接近，水位变化呈现极大相关性，由于观测时间的不同，略有位移。线性相关系数R为0.988 6，光谱角SAM=0.000 048。两组数据的高度相关性表明测高数据质量高。

图7 ENVISAT#571和#786轨迹推算的水位时间序列

3.2 水位变化分析

总的来说，萨德湿地的平均水位变化幅度随空间分布而呈现分异(如图8所示)。其水位变化分异分为3种不同类型。其中类型一最为常见(如图9所示)，空间上沿白尼罗河沿岸分布，可以看到水位较低的年份为2009—2010和2006—2007年，而在2002—2006年水位保持较高水平。而另外两种类型分布在白尼罗河支流地区，对于类型二(如图10所示),2002—2006水位相对类型一处于较低水平，2010年份水位下降明显；类型三(如图11所示)的干旱低水位年份为2002, 2004—2006, 2009—2010, 2011—2013，从2002年水位就持续走低，并在2005年达到研究期间的最低水位。水位变化的差异性表明了萨德湿地的全境水源供给并不单一。沿白尼罗河沿岸，水流供给主要来自河流。其他支流区域的水源供给更多的受到气候和周围环境的影响。

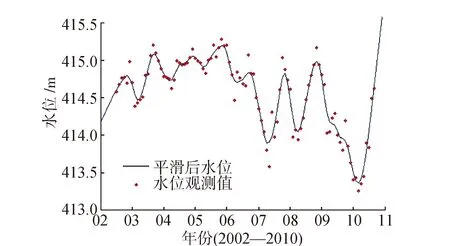
图8 类型一：白尼罗河沿岸水位变化图(萨德湿地南部)

图9 类型二：白尼罗河支流水位变化图(萨德湿地中部)

图10 类型三：支流水域沿岸水位变化图(萨德湿地北部)

图11 萨德湿地平均水位变化幅度

本研究可以发现4个现象：1)水位变化有很强的季节节律性；2)沿白尼罗河分布的水域以及位于白尼罗河支流的水域水位变化规律在呈现较大的分异的同时，各自呈现出区域性相似的变化规律；3)平均水位变化的幅度最高达到1.2 m，自南向北水位幅度变化逐渐减弱；4)2009—2010年全区域的水位都呈现明显下降，部分区域水位在2006—2007年也明显低于平均值。

3.3 维多利亚湖、阿尔伯特湖与萨德湿地南部水位对比分析

萨德湿地位于白尼罗河沿岸，受白尼罗河水位变化影响显著，而维多利亚湖是白尼罗河最重要水源供给，本文选取Sudd南部白尼罗河沿岸网格与维多利亚湖水位(下载于DAHITI(Schwatke et al. 2014, Schwatke et al. 2015b))进行对比，预期得到较高相关性，结果发现相关性很低(R=-0.152 0，SAM=0.001 1)，查看文献发现，2002—2006年，2009—2010年都是旱灾，但是维多利亚湖附近欧文瀑布大坝(Owen Falls)过度放水发电[12]，导致水位下降严重，而Sudd由于白尼罗河补水增多，旱灾水位不降反升。2005年维多利亚湖达到1951年以来史上最低，为保护湖泊，大坝的发电受到制约，开闸放水大量减少，白尼罗河补水减少，当遭遇2009—2010年旱灾时，维多利亚湖水位略减，萨德湿地的水位却大大下降了。

为验证这一说法，本文又对位于欧文瀑布大坝下游萨德湿地上游的阿尔伯特湖水位和萨德湿地南部水域水位变化进行对比分析，结果表明，二者水位具有很强的相关性(R=0.775 7以及SAM=0.000 182.)。

4 结束语

卫星测高对大型湿地的研究有很大的应用前景，尤其是对于难以实地观测的大型湿地，利用卫星测高可以对湿地水位变化进行观测和研究，进而可对湿地的洪泛机制进行探索。随着更高时空分辨率的测高卫星(Sentinels, SARAL和SWOT)的发射，卫星测高对内陆水域的应用前景会更加广阔。值得一提的是，高分七号卫星，也搭载激光测高仪，预计2018年发射。

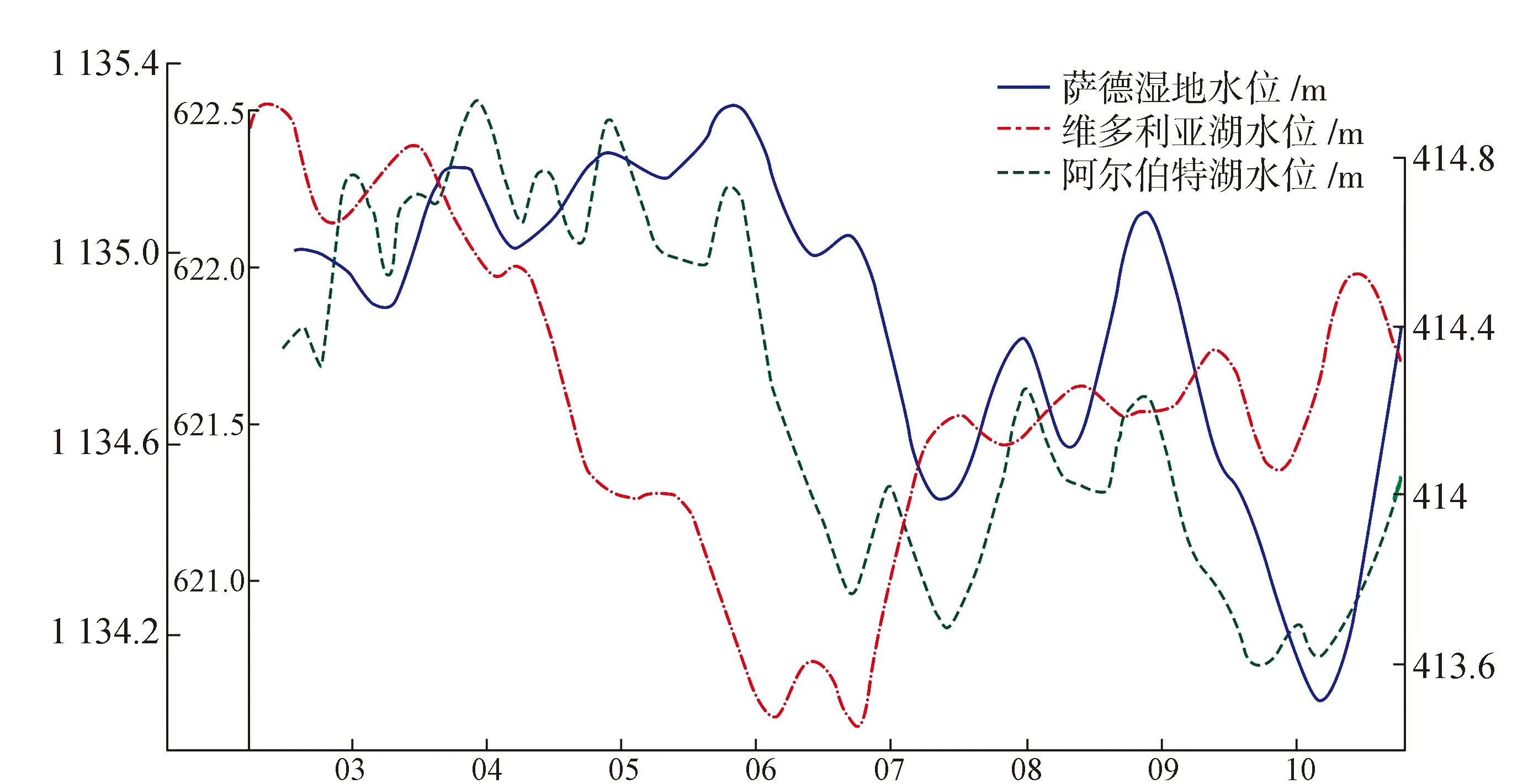
图12 维多利亚湖(红)、阿尔伯特湖(绿)与萨德湿地南部水位(蓝)对比图

但是，卫星测高的应用推广仍存在几个问题，一是回波重定和奇异值剔除等算法的普适性还较弱，需要针对研究区域进行较多试验；二是由于测高雷达数据足径(footprint)较大，遇到非均质、复杂下垫面的研究区，其反演精度将大打折扣；三是本文由于萨德湿地地势平缓，地形影响不大，但对于地势高程变化较大湿地地区，必须辅以高精度地表模型进行地形校正；四是当应用于大型湿地的研究时，卫星测高和其他遥感技术一样，其结果的精度检验是一大难题。由于大型湿地的水位实测数据匮乏，其他间接辅助数据(例如GRACE卫星的地球重力场数据以及全球降雨量等相关数据)分辨率过低，进行精度评价可靠性不高。