三峡工程与两湖河川径流丰枯遭遇研究
(长江勘测规划设计研究有限责任公司,湖北 武汉 430010)
《中共中央国务院关于加快推进生态文明建设的意见》和《长江经济带发展规划纲要》指出,要加强洞庭湖、鄱阳湖等重点湖泊生态安全建设。洞庭湖和鄱阳湖作为我国最大的两个淡水湖泊,是长江经济带、洞庭湖生态经济区、鄱阳湖生态经济区等国家战略的重要依托。极端水文事件已经成为限制社会经济可持续发展的瓶颈,导致水资源量时空分布不均[1]。由于江湖环衔,长江干流的水文情势变化势必会导致两湖产生连锁反应。因此,分析长江干流三峡工程与两湖地区天然径流丰枯遭遇规律对保障两湖水安全可提供理论支撑。
已有相关学者开展了关于两湖地区水文气象、水沙等方面的研究[2-4],取得了丰富的成果。周念清等[5]构建了洞庭湖的入出湖年径流量、年输沙量Copula联合分布函数,对水沙丰枯遭遇进行了分析;孙鹏等[6]选取鄱阳湖流域主要支流洪水和枯水流量,构建联合分布函数分析了流域的极值流量遭遇特征;张忠波等[7]利用联合分布模型对三峡工程供水期相邻时段丰枯遭遇变化进行了研究。关于三峡工程与两湖不同时期(全年期、汛期和非汛期)的天然径流丰枯遭遇研究比较少见。因此,本文利用多种统计技术对三峡工程水文控制站和洞庭湖、鄱阳湖的入湖控制站的天然河川径流进行趋势诊断,构建三峡工程和两湖入湖控制站天然河川径流的Copula联合分布模型,分析三峡工程与洞庭湖、鄱阳湖天然径流丰枯遭遇概率特征,为三峡水库供水调度减轻两湖地区供需矛盾的研究提供理论参考。
1 研究区域概况及资料
三峡工程作为长江流域的控制性骨干工程,对下游两湖地区的防洪、水资源安全具有关键作用。洞庭湖和鄱阳湖位于长江中游南岸,是中下游水资源的重要来源。三峡工程坝址宜昌代表站、洞庭湖区和鄱阳湖入湖控制站湘潭站、外洲站多年平均降水量分别为1 137.3,717.6,931.1 mm,年平均天然径流量为4 720亿,703亿,756亿m3。三峡工程与两湖地理位置示意如图1所示。
2 研究方法
2.1 趋势诊断
本研究对于天然河川径流长序列趋势诊断采用线性回归[8]、Spearman秩检验[9]和Kendall秩和检验[10]3种常用方法。
2.1.1线性回归
针对气象变量与时间之间的线性相关关系来描述序列中可能存在的趋势变化,气象要素x为因变量,时间t为自变量,线性相关关系r:
(1)

2.1.2Spearman秩检验
通过分析气象序列的秩与时间之间回归关系进而在给定置信度水平下检验趋势变化。变量序列xt与时间t的秩序τt,t=1,2,…,n,则秩相关系数计算公式为
(2)
类似地,t检验法对秩相关系数r进行显著性检验,统计量为
(3)
2.1.3Kendall秩和检验
Kendall秩和趋势检验统计量公式为
(4)
(5)
-1)(2th+5)]/18
(6)
(7)
式中,k为变量序列含有的相等数据的组数;th为第h组相等数据个数;当n>10时,E(S)=0;统计量Z在零假设下服从标准正态分布,原假设为无趋势。
2.2 Copula联合分布模型
2.2.1丰枯等级划分
丰枯等级划分依据水利部颁布的相关规定,本次研究以37.5%和62.5%来定义丰、枯频率(见表1)。

表1 丰、平、枯等级划分Tab.1 Classification for wet year, partially wet year, normal year, partially dry year, and dry year
2.2.2边缘分布模型
本文选取国内外常用的4个边缘分布模型,分别为皮尔逊III 型分布(P-III)、广义极值分布(GEV)、Logistic 分布(GLO)和对数正态分布(LN),关于各个边缘分布模型及估计参数详细的介绍见参考文献[11]。
2.2.3Copula联合分布模型
本文通过三峡工程坝址控制站与两湖入湖控制站天然径流量变量联合分布来构建Copula模型。联合分布模型的优势在于不需要要求独立变量服从相同的边缘分布,边缘分布中的各种信息将不会丢失。因此Copula函数被广泛用于多变量水文频率联合分布研究[12-15]。联合分布概率计算公式为
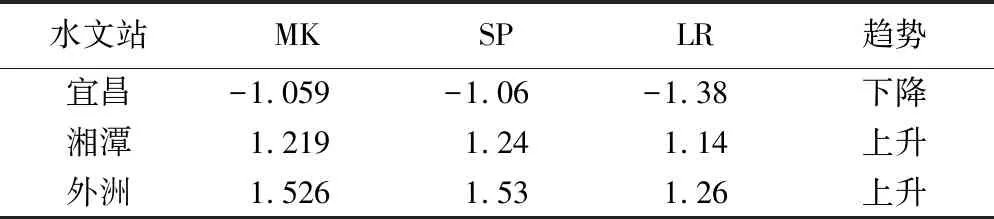
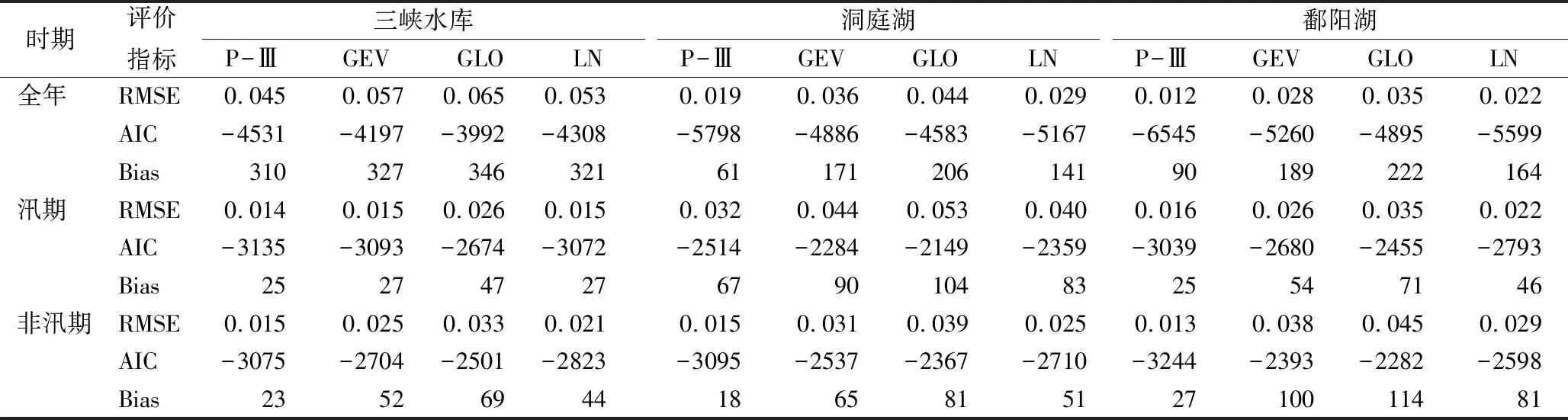
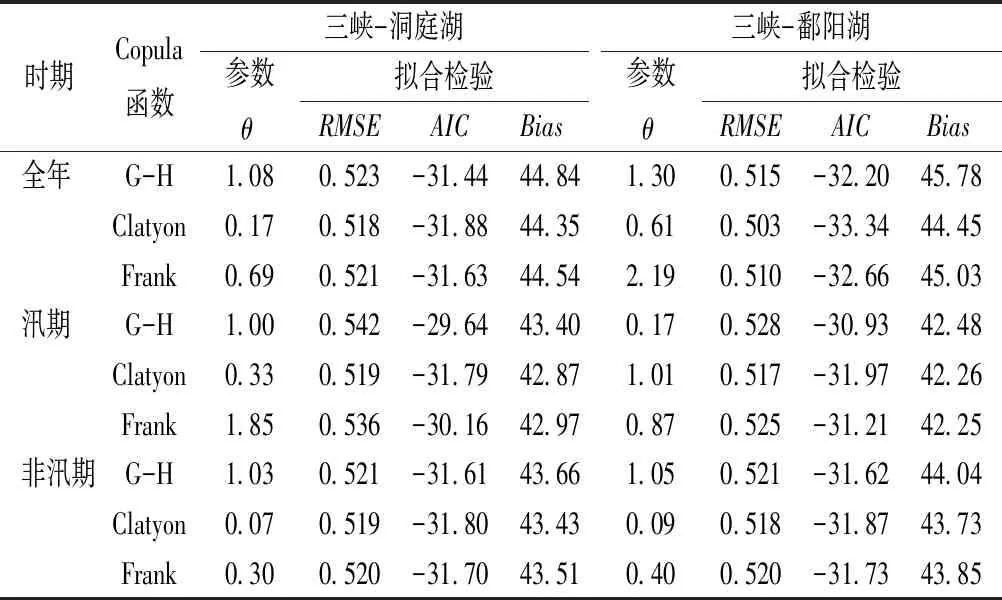
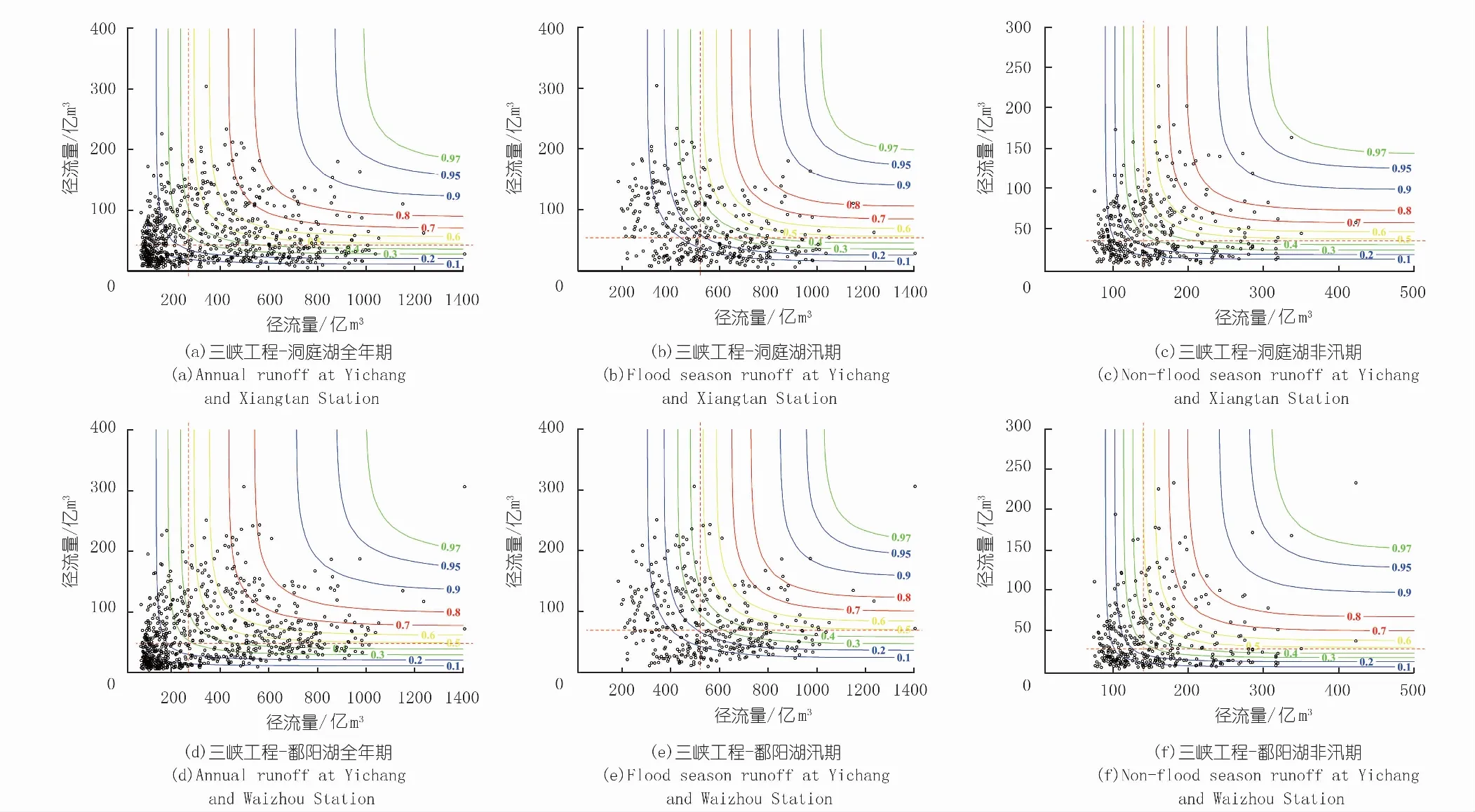
P(x1≤x F(x1,y2)-F(x2,y2)+F(x1,y1) (8) 式中,x1,x2和y1,y2分别为三峡工程坝址控制站和两湖入湖控制站不同时期不同频率径流阈值[16]。 本研究使用3个被广泛使用于水文多变量频率计算中的Archimedean Copula函数,分别为Gumbel-Hougaard (G-H) Copula, Clayton Copula和Frank Copula,函数及其参数θ与Kendall秩相关系数τ的关系如表2所示。 2.2.4模型优选 在95%置信度水平下,采用Kolmogorov-Smirnov(KS)检验方法对联合分布进行检验[16]。利用均方根误差(RMSE)、AIC准则(Akaike Information Criterion)和Bias 3种常用的拟合度评价方法对边缘分布和联合分布模型进行优选[17-19]。 (9) (10) (11) 式中,pei和pi分别表示经验和理论概率,N为气象序列的样品大小,M为时变边缘分布和Copula模型的评估参数个数。 利用线性回归法(LR)、Spearman秩检验(SP)和Kendall秩和检验(MK)3种方法对三峡工程坝址控制站、两湖入湖控制站1956~2016年天然年径流序列进行趋势诊断。如表3和图2所示,宜昌控制站天然年径流量呈现不显著下降趋势,湘潭、外洲控制站天然年径流量呈现不显著增大趋势。如图2中纵坐标所示,上游宜昌站天然年径流最小值为2 941亿m3,较下游湘潭、外洲控制站的天然年径流最大值1 103亿,1 205亿m3要大。年径流序列的线性趋势和滑动平均分析如图2所示。 表3 径流序列的趋势分析结果Tab.3 Statistical results of trend analysis in rainfall time series 3.2.1边缘分布模型 利用P-III、GEV、GLO和LN 4个边缘分布函数对三峡工程坝址控制站、两湖入湖控制3个不同时期(全年、汛期和非汛期)的天然径流量进行拟合模拟,边缘分布参数及K-S检验结果如表4所示。在95%置信度水平下,三峡工程和两湖区天然径流量边缘分布均通过了假设检验。天然径流量边缘分布频率拟合曲线如图3所示,P-Ⅲ分布3个拟合精度评价指标(RMSE、AIC和Bias)均较小,表明P-Ⅲ分布拟合效果更好。 表2 Archimedean Copula函数及其参数θ与Kendall秩相关系数τ的关系Tab.2 Forms of copula functions and parameter estimation formula 图2 三峡工程、洞庭湖和鄱阳湖河川径流序列趋势变化Fig.2 Runoff of trend analysis of Three Gorges Project,Dongting Lake and Poyang Lake 时期评价指标三峡水库P-ⅢGEVGLOLN洞庭湖P-ⅢGEVGLOLN鄱阳湖P-ⅢGEVGLOLN全年RMSE0.0450.0570.0650.0530.0190.0360.0440.0290.0120.0280.0350.022 AIC-4531-4197-3992-4308-5798-4886-4583-5167-6545-5260-4895-5599 Bias3103273463216117120614190189222164 汛期RMSE0.0140.0150.0260.0150.0320.0440.0530.0400.0160.0260.0350.022 AIC-3135-3093-2674-3072-2514-2284-2149-2359-3039-2680-2455-2793 Bias2527472767901048325547146 非汛期RMSE0.0150.0250.0330.0210.0150.0310.0390.0250.0130.0380.0450.029 AIC-3075-2704-2501-2823-3095-2537-2367-2710-3244-2393-2282-2598 Bias23526944186581512710011481 图3 三峡工程、洞庭湖与鄱阳湖3个不同时期径流量边缘分布频率曲线拟合Fig.3 Fitted marginal probabilities plots of theoretical and empirical probabilities of annual,flooding season and non-flood season for Three Gorges Project, Dongting Lake and Poyang Lake 3.2.2Copula联合分布模型 构建G-H Copula, Clayton Copula和Frank Copula 3个二维Copula联合分布模型,三峡工程与两湖径流量联合分布参数估计及评价结果如表5所示。从三峡工程与洞庭湖、鄱阳湖全年、汛期和非汛期3个不同时期径流量Copula联合分布拟合评价精度来看,Clayton Copula的RMSE、AIC和Bias 3个评价指标均较小,说明拟合精度较高。因此,Clayton Copula模型可以更好地模拟三峡工程与两湖径流量序列之间的独立结构。 表5 三峡工程、洞庭湖与鄱阳湖3个不同时期径流量Copula联合分布参数估计及评价结果Tab.5 Estimated parameters of joint distribution model and the goodness-of-fit results of Copulas of annual,flooding season and non-flood season 本研究丰、枯频率按37.5%和62.5%定义,利用构建的Copula联合分布模型计算三峡工程与两湖径流量丰枯遭遇概率,全年、汛期和非汛期3个不同时期径流量遭遇的联合分布等值线如图4所示。以全年期为例,从等值线图中可以得出以下结果。 (1) 当三峡工程控制站径流量小于180亿m3,且洞庭湖入湖控制站径流量小于31亿m3时,三峡工程与洞庭湖径流量全年期遭遇同枯的概率为11.74%;当三峡工程控制站径流量小于391亿m3,且洞庭湖入湖控制站流量小于60亿m3时,三峡工程与洞庭湖径流量全年期遭遇同丰的概率为42.10%。 (2) 从丰枯不同步遭遇的角度来分析,三峡丰洞庭湖枯、三峡枯洞庭湖丰的全年期遭遇概率分别为23.54%和19.65%。同样,可以分析得出三峡工程与洞庭湖径流量汛期遭遇同枯和同丰的概率分别为6.28%和35.06%,三峡丰洞庭湖枯汛期遭遇概率为15.58%、三峡枯洞庭湖丰的汛期遭遇概率为17.98%。三峡工程与洞庭湖径流量非汛期遭遇同枯和同丰的概率分别为11.31%和40.22%,三峡丰洞庭湖枯汛期遭遇概率为23.15%,三峡枯洞庭湖丰的汛期遭遇概率为19.12%。类似地,以三峡工程与鄱阳湖径流量遭遇情况分析可以得出:① 当三峡工程控制站径流量小于180亿m3,且鄱阳湖入湖控制站径流量小于35亿m3时,三峡工程与鄱阳湖径流量全年期遭遇同枯的概率为16.62%;当三峡工程控制站径流量小于391亿m3,而且鄱阳湖入湖控制站流量小于65亿m3时,三峡工程与鄱阳湖径流量全年期遭遇同丰的概率为44.71%;② 从丰枯不同步遭遇的角度来分析,三峡丰鄱阳湖枯、三峡枯鄱阳湖丰的全年期遭遇概率分别为28.45%和22.71%。同样,可以分析得出三峡工程与鄱阳湖径流量汛期遭遇同枯和同丰的概率分别为10.05%和36.25%,三峡丰鄱阳湖枯汛期遭遇概率为19.45%、三峡枯鄱阳湖丰的汛期遭遇概率为20.11%;三峡工程与鄱阳湖径流量非汛期遭遇同枯和同丰的概率分别为11.41%和40.72%,三峡丰鄱阳湖枯汛期遭遇概率为22.83%、三峡枯鄱阳湖丰的汛期遭遇概率为19.62%。 图4 三峡工程与两湖3个不同时期径流量遭遇的联合分布等值线Fig.4 Contours of joint distribution between Yichang Station and Xiangtan,Waizhou Stations 从时间尺度来看,丰枯同步的频率在非汛期要高,一般而言,丰枯同步尤其同枯情况下不利于供水,这对非汛期十分缺水的受水区来说是不利的,三峡与两湖同枯的概率都小于10%,理论上保证了供水的可能性;从空间尺度上来看,三峡与两湖丰枯同步的概率相当,三峡与鄱阳湖的丰枯异步概率较洞庭湖略大;当三峡丰洞庭湖或鄱阳湖枯时为最有利三峡供水情景,全年期、汛期和非汛期遭遇概率分别为32.44%,26.01%,30.38%和36.38%,28.69%,31.38%。由于三峡工程与两湖相距距离不同,距离越近径流在时间上分配就相对一致些,反而越不利于供水。三峡与两湖同枯遭遇概率越大,三峡工程实施供水越不利,三峡工程与洞庭湖和鄱阳湖全年期同时遭遇枯水的概率分别为11.74%和16.62%;汛期同时遭遇枯水的概率分别为6.28%和10.05%;非汛期同时遭遇枯水的概率分别为11.31%和11.41%。 本研究利用多种统计技术对三峡工程坝址控制站与两湖入湖控制站天然径流序列进行了趋势诊断。诊断结果表明:宜昌站呈现不显著下降趋势,湘潭、外洲站呈现不显著增大趋势;构建了多种边缘分布和Copula联合分布模型,并采用多种拟合精度评价方法优选出拟合精度较高的边缘分布和联合分布。利用优选构建的Copula模型计算分析三峡工程与两湖天然径流量丰枯遭遇概率及其变化规律。研究表明三峡工程与鄱阳湖丰枯遭遇概率较洞庭湖略大。全年期三峡工程与洞庭湖、鄱阳湖遭遇同丰同枯概率较汛期、非汛期要大,同丰同枯概率分别为42.10%和44.71%,同枯概率分别为11.74%和16.62%。三峡工程与两湖丰枯异步遭遇概率较同步概率要小。进一步研究了三峡工程实施供水最有利情景即三峡丰两湖枯时遭遇概率及其变化规律。研究结果可为定量认识三峡工程与两湖水量丰枯遭遇的发生频率以及减轻两湖地区供需矛盾的三峡水库供水调度研究提供理论参考。 考虑到人类活动和气候变化影响,未来要进一步研究非一致性条件下丰枯遭遇变化规律,识别引起变化的影响因子,制定不同情景下联合供水的供水调度方案,为提高三峡对两湖地区供水的效益提供基础。3 结果及分析
3.1 趋势分析
3.2 Copula联合分布模型构建



3.3 基于Copula理论的三峡工程与两湖径流量丰枯遭遇分析
4 结 论

