层次—模糊分析法在重力式挡土墙评估中的应用

王 威，杨正玉，刘顺青，黄贝贝，武 旻

（1.江苏省地质矿产局第三地质大队，江苏镇江212001；2.江苏科技大学土木工程与建筑学院，江苏镇江212005）

近年来各类工程安全评估方法的研究已成为工程界和学术界的热点问题［1］。挡土墙安全评估方面，万国环等［2］通过对重力式挡土墙安全性各要素进行打分，最后根据分值确定挡土墙的安全等级；杨昊等［3］对挡土墙的检测数据进行系统分类和评估，得到了一套针对挡土墙综合质量的安全评估标准； 陈立国等［4］针对重力式挡土墙，采用地质雷达的质量检测结果对其综合质量安全进行了分类评估； 张秀等［5］引入定性与定量评估相结合的手段，提出了挡土墙综合安全评估法。但是上述评估方法研究成果单一，不易操作和推广。

本文基于层次—模糊数学综合安全评估法［6］，建立了一套评估重力式挡土墙的安全指标体系，用于定量评价重力式挡土墙的运营状况。研究结果对正确地认识重力式挡土墙的运营现状，提高挡土墙的总体安全具有重要意义。

1 重力式挡土墙安全评估指标体系

1.1 指标体系的构建

参考文献［7］中指标体系的选取，本文选取表观情况、材质情况、受力情况作为重力式挡土墙安全评估的三大类指标，同时利用层次分析法对每一类指标进行二级划分，如图1。

1.2 评价目标的划分

重力式挡土墙安全评估系统中评价指标是分析系统的基础。参照已有的文献［1，8］，结合重力式挡土墙的特点，本文评价指标及评估目标都采用6级划分法，为良好、较好、一般、较差、差、危险，相应的评定标度分别为6，5，4，3，2，1。

图1 重力式挡土墙安全评估指标体系

2 重力式挡土墙安全评估模型

本文采用两级的模糊综合评价模型计算重力式挡土墙的安全评估指标体系。在该评价模型中，从分项指标层出发，首先一级模糊指标层的各个指标，而后二级模糊评价指标层。

2.1 一级模糊综合评价

2.1.1 评价指标集的建立

根据重力式挡土墙安全评估指标体系（图1），有Ai=（b1，b2…bn），i=（1，2，3），其中Ai为指标层的各个因素，bi为分项指标层的各个因素。

2.1.2 评价集合的建立

将重力式挡土墙的评价指标划分为6个等级（如前所述），分别采用安全等级向量v1，v2，v3，v4，v5，v6代表各评价指标。

2.1.3 单因素评价矩阵的确定

当x在研究的范围中变动时，A（x）为一函数，称为A的隶属函数。隶属函数为模糊数学的本质，可定量评估模糊事物的基础。采用隶属函数建立各分项指标bi对评价集合的隶属向量Rbi，表示为Rbi=（Rbi1，Rbi2，…，Rbi6）。而单因素评价矩阵R′bi由隶属向量建立，表示对指标层各因素的评价。

2.1.4 一级模糊的评价结果

模糊综合评价过程其实就是通过模糊算子和隶属函数建立一个评价模型。而模型的建立与矩阵相乘相对应，通过各单因素评价矩阵R′bi与其权重WAi相乘得到各因素Ai对评价集合的V的隶属向量。

2.2 二级模糊综合评价

将一级模糊评价结果集组成二级模糊评价的单因素评价矩阵，并乘以相应的权重向量，得到二级模糊评价结果——目标因素对评价集的隶属向量R，表示为R=W×（RA1，RA2，RA3）T。

2.3 模糊向量单值化

根据前文的分析，重力式挡土墙安全等级准则如表1。

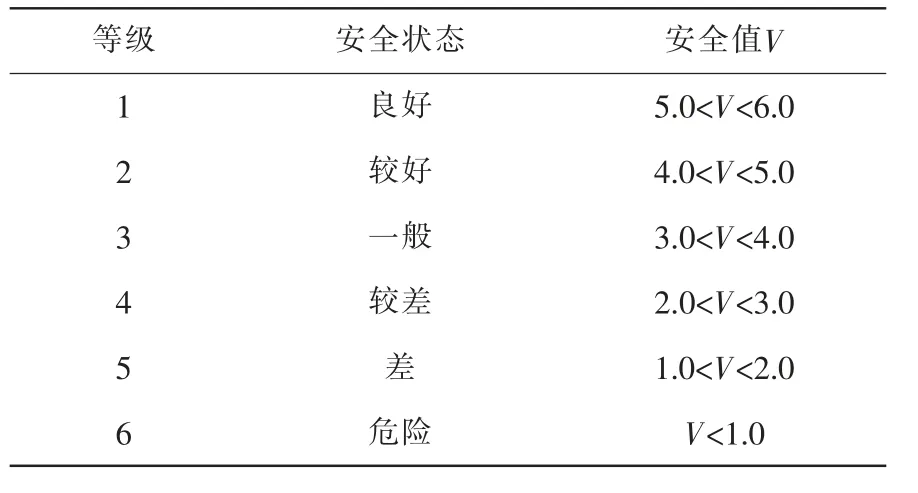
表1 重力式挡土墙安全等级准则

3 工程实例

3.1 一级模糊评价

以镇江城区某重力式挡土墙为例，邀请地灾专家分别对该重力式挡土墙进行一级和二级指标打分，求得了以下权重。

一级指标U1=（表观情况、材质情况、受力情况）的权重W=（0.24，0.30，0.46）。

二级指标U12=（墙身、墙顶、基础、伸缩缝、排水设施）的权重W12=（0.28，0.16，0.26，0.14，0.16）。

以此类推，计算出U22=（片石、砂浆） 的权重W22=（0.72，0.28），U32=（裂缝、位移）的权重W32=（0.24，0.76）。

采用隶属函数建立该挡土墙各二级指标安全等级的隶属向量，计算结果如表2。

表2 二级指标隶属向量

续表2

由表2中二级指标隶属向量为行组成单因素评判矩阵R′A1，则此时相应的R′A1=［R11，R12，R13，R14，R15］T，将权重向量W12与R′A1进行运算，可得到重力挡土墙表观情况安全等级的隶属向量RA1。

将二级权重向量与单因素评判矩阵进行模糊运算，可以得到一级指标安全等级的隶属向量。以表观情况为例，单因素评判矩阵为：

将权重向量W12与单因素评判矩阵进行模糊运算，可确定重力式挡土墙表观情况安全等级的隶属向量RA1。

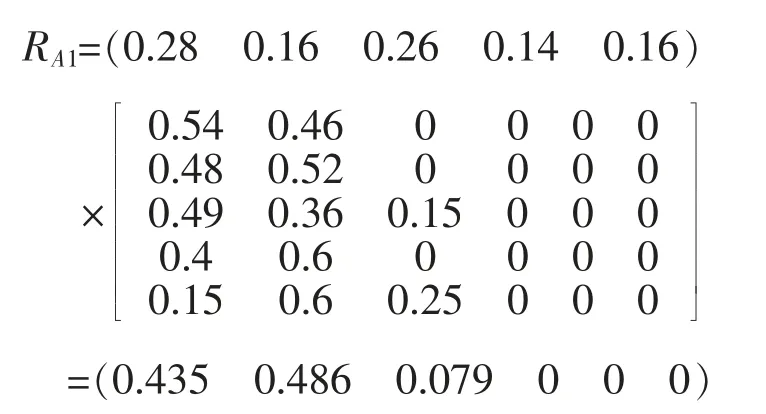
采用同样的方法，可计算得到材质情况及受力情况安全等级的隶属向量RA2和RA3。

3.2 二级模糊评价

将重力式挡土墙的表观情况、材质情况、受力情况安全等级的隶属向量构成二级模糊评价分析矩阵RA。

将权重向量W与二级模糊评价分析矩阵进行模糊运算，可确定重力式挡土墙安全等级现状的隶属向量R。

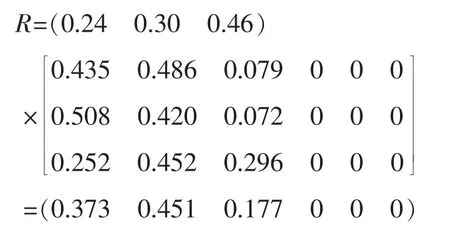
最后可得到重力式挡土墙的综合分值：

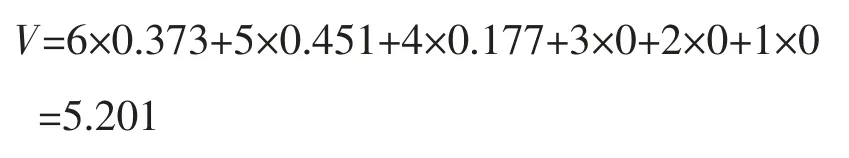
根据表1，5.0

4 结语

（1）综合考虑了影响重力式挡土墙安全的因素，采用层次分析法构建了其安全评估指标体系。

（2）提出了针对重力式挡土墙的层次—模糊分析法，该方法可将评估结果进行量化，使得评估结果更为准确。