欠平衡连续油管钻井中螺旋管段气液两相流摩阻压降特性研究

冯金禹，闫 铁，孙士慧，唐海燕，田 龙

(1.东北石油大学，黑龙江 大庆 163318；2.中国石油大庆油田有限责任公司，黑龙江 大庆 163511；3.中国石油新疆油田分公司，新疆 克拉玛依 834000)

0 引 言

连续油管钻井是一种新型的、低成本的钻井方式[1-5]。但在欠平衡连续油管钻井中，两相流在螺旋管段的摩阻压降难以确定，导致地面泵压以及其他相关水力参数计算困难。国内外许多学者对于流体在螺旋管段上的流动特性和摩阻压降特点进行了研究。Dean等[6]对螺旋管内液体的流动进行了实验研究，提出了狄恩数的定义，用于衡量离心力对流动的影响。Berger等[7]给出了牛顿流体在螺旋管内流动的摩阻压降系数的计算式。GUO等[8]以水为工质，对不同干度条件下，不同曲率比的螺旋管段内气液两相流流动特性进行了实验研究，根据实验数据给出了摩阻压降的实验关联式。陈勋等[9]利用流体力学原理，结合现场数据，推导出压裂液在螺旋管段的摩阻压降计算公式。张晋凯等[10]利用数值模拟方法，分析了液体在连续油管螺旋管段的流动特性，给出了摩阻压降计算经验公式。王洪涛[11]在实验的基础上对幂律流体在连续油管螺旋管段的流动特性以及摩阻压降进行了研究，并对经验公式进行了优选和分析。虽然相关交叉学科的学者对于螺旋管段内两相流的流动特性进行了研究，但大多局限于各自的实验特点，在工程上并不具有很好的通用性。目前国内外鲜见专门针对连续油管螺旋管段的气液两相流摩阻压降特性的研究。此次研究通过数值模拟方法，针对连续油管钻井的工程特点，研究了气液两相流在连续油管螺旋管段的流动特性，分析了影响连续油管螺旋管段摩阻压降的相关因素。

1 物理模型与网格划分

如图1所示，滚筒上的连续油管具有重复性，为便于计算和描述，只选取了其中的一段进行研究，称之为单元螺旋管段。单元螺旋管段参数为：连续油管的外半径为38.1 mm，内半径为30.2 mm；滚筒半径为1 219.2 mm。应用ICEM软件对物理模型进行网格划分，其中，入口和出口处进行O型剖分，边界层处网格进行适当加密，以保证求解的准确性(图2)。

图1 连续油管滚筒示意图

图2 物理模型网格划分示意图

2 数值模拟

2.1 两相流模型

当黏性流体流过螺旋管段时，由于离心力的作用，在管道截面上形成与主流方向垂直的流动，即二次流现象，影响螺旋管段内流体的流动。同时，由于两相流界面的存在，以及由此产生的质量、动量和能量的交换中，气液两相均处于不平衡的状态，各种参数也无法统一[12]。Fluent软件中欧拉-欧拉两相模型将气液看成相互贯穿的连续流，在任一空间内，各相的体积率之和为1，且各相都具有独立的守恒方程组，能够准确求解螺旋管段内两相流的流动参数[13]。因此，采用欧拉-欧拉模型进行求解。

2.2 控制方程

质量守恒方程：

(1)

式中：αi为流体的体积分数；ρi为流体的密度，kg/m3；ui为流体的速度矢量，m/s；下标i表示气相或液相。

动量守恒方程：

(2)

式中：pi为流体的热动力压力，Pa；τi为流体的压力应变张量；g为重力加速度，m/s2。

2.3 初始条件与求解方式

应用Fluent软件对模型进行数值模拟求解，选择压力基求解器，多相流模型选择欧拉-欧拉模型，湍流模型选择标准k-ε模型[14]。选择水为液相，密度为998.200 kg/m3，黏度为1.003 00 mPa·s；选择氮气为气相，密度为1.138 kg/m3，黏度为0.016 63 mPa·s，气液体积比为30∶1。

入口采用速度入口方式，入口速度为10 m/s，出口采用压力出口方式，压力设置为1.5 MPa。采用高斯格林迭代格式，选择交错压力差分格式，采用一阶迎风离散格式离散。为简化分析，管壁粗糙度设为水力光滑，并且在靠近壁面处使用加密网格，其中，速度入口采用边界法向方式，并设定壁面边界为静止壁面和无滑移壁面。

3 数值模拟结果及流动特性分析

图3为数值模拟计算后得到的螺旋管段截面云图，图中ex表示螺旋管段外侧，in表示螺旋段内侧。由图3a、b可知，流体速度由螺旋管段内侧向外侧呈阶梯状分布，越靠近内侧，流体的速度越大，这是由于流体自身具有黏性力的作用，同时，流体又受到离心力的影响，主流核心区并不在管道的中轴线上而是向管道的外侧偏移。由图3c、d可知，无论气相还是液相，压力均呈现由管道内侧向外侧逐渐增高的趋势，此时管道外侧的压力高于内侧，在内外侧压力差的作用下，部分流体会从管外侧高压区域向内侧低压区域流动。由图3e、f可知，由于管道内外侧存在压差，在管道截面上形成了与主流方向垂直的流动，这种不同于主流方向的流动，通常称之为二次流。正是由于这种垂直于主流方向的二次流存在，阻碍了主流方向上的流体流动，影响连续油管螺旋段的摩阻压降的大小。

图3 螺旋管段截面云图

4 连续油管螺旋段摩阻压降影响因素分析

4.1 充气量对摩阻压降的影响

物理模型中液相设置为水，气相设置为氮气，出口压力设置为1.5 MPa。根据文献[15]，质量充气量(气相质量占流体总质量的比例)分别选择0.22、0.27、0.36、0.63，在不同的入口速度(v)条件下进行数值模拟计算(图4)。

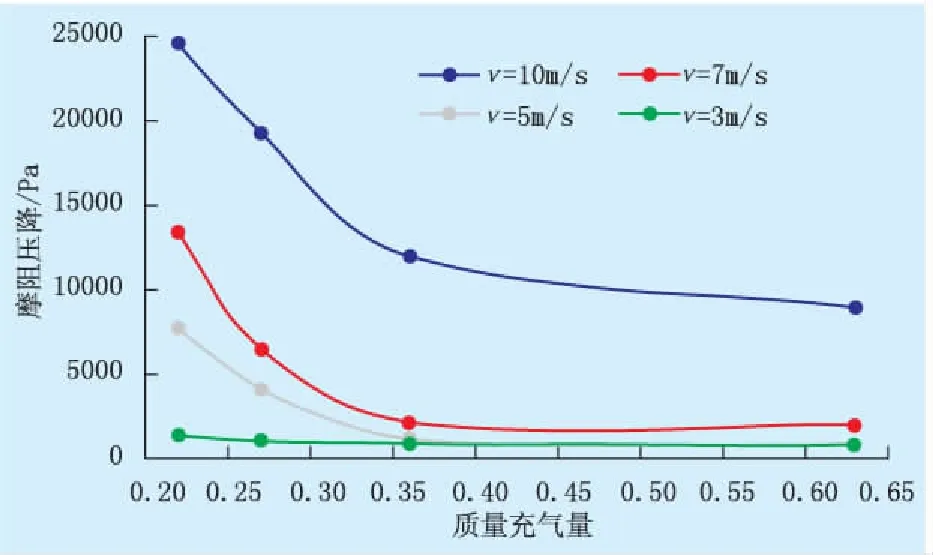
图4 充气量与连续油管螺旋管段摩阻压降的关系

由图4可知：在入口速度一定的条件下，随着充气量的增大，气相的含量增大，摩阻压降随之减小，但随着充气量的逐渐增大，摩阻压降减小的趋势明显减缓。这是由于随着管内气相含量逐渐增加，气相产生的摩阻压降占总压降的比例越来越大，且逐渐趋于稳定。通过图5可知，在相同充气量和压力条件下，随着入口速度的减小，摩阻压降也随之减小。

4.2 钻井液物性对摩阻压降的影响

根据文献[16-17]，选择4种不同物性的钻井液作为液相，钻井液物性参数见表1。入口速度设置为10 m/s，出口压力为1.5 MPa，气相均选择氮气，选择不同的质量充气量进行数值模拟计算(图5)。

表1 钻井液物性参数

图5 钻井液物性参数与连续油管螺旋管段摩阻压降的关系

由图5可知：无论采用何种钻井液，随着充气量的增大，摩阻压降均减小；通过对比钻井液A和钻井液C可知，在黏度、充气量相同的条件下，钻井液的密度越小，摩阻压降越小；通过对比钻井液B和钻井液C可知，在密度、充气量相同的条件下，液相钻井液的黏度越大，摩阻压降越大；通过对比钻井液B和钻井液D可知，虽然钻井液B和钻井液D密度接近，但由于2种钻井液的黏度差值较大，摩阻压降的差值相差也较大，可见钻井液黏度与钻井液密度相比，前者对于螺旋管段摩阻压降的影响更为显著。

4.3 螺旋管段曲率比对摩阻压降的影响

由于工程中使用的连续油管和滚筒的规格不尽相同，因此，研究曲率比(连续油管内径与滚筒内径之比)对螺旋管段摩阻压降的影响，对工程应用有重要的意义。

根据文献[18]，选取曲率比为0.012、0.016、0.022、0.035，水为液相，氮气为气相，气液体积比为30∶1，出口压力设置为1.5 MPa。设置不同的入口速度进行数值模拟计算(图6)。由于不同曲率的连续油管单元螺旋管段的长度不同，摩阻压降无法进行直接比较，因此，纵坐标采用单位长度摩阻压降进行表示。

图6 螺旋管段曲率比与连续油管螺旋管段摩阻压降的关系

由图6可知：随着连续油管螺旋管段的曲率比增大，管内的摩阻压降随之增大，这是由于随着曲率比的增大，流体受到的离心力变大，二次流现象明显，对主流方向的流体流动的阻碍作用加大，螺旋管段的摩阻压降随之增大；入口速度较小时，曲率比对于摩阻压降的影响并不大。

5 结 论

(1) 两相流在螺旋管段中流动时，由于螺旋管内侧区域和外侧区域压力不同，会在垂直于管道主流方向形成二次流，阻碍流体流动，这是螺旋管段摩阻压降较大的主要原因。

(2) 螺旋管段的摩阻压降随充气量的增大而减小；在相同充气量的条件下，摩阻压降随液相钻井液的密度和黏度的增大而增大。现场施工时，应在满足工程要求的条件下，适当增大充气量，并尽量选择黏度低、密度小的钻井液。

(3) 螺旋管段的摩阻压降随螺旋管的曲率比的增大而增大，在施工时，在管径相同的情况下，连续油管应尽量选择缠绕在滚筒半径较大的滚筒上进行作业。