蒙特卡罗模拟技术在计量经济学教学中的应用
韩猛
(内蒙古财经大学统计与数学学院,呼和浩特010070)
0 引言
借助计算机驱动的随机模拟技术来讲授计量经济学是帮助学生加深理解计量经济学理论方法的有效途径之一。通常,对于刚开始接触计量经济学理论的学生而言,因为理论的复杂性或理解能力的差异,准确地理解相关理论并不是一件容易的事情。这个时候,我们往往需要借助经验方法来帮助学生加深理解,这就要求我们必须找到若干合理的实际案例,但这通常是一个不可能的提议。因此,通过蒙特卡罗模拟技术来生成符合我们模型设定的数据就成了一种可行的有效方法。
本文重点演示了计算机编程和蒙特卡罗模拟技术如何为计量经济学理论教学服务。为了实现这一目标,本文将以案例的形式展示评估计量经济学教学过程中普通最小二乘估计量的统计性质以及基于R 的基本实现问题。
Mooney(1997)最早提出了关于蒙特卡罗模拟技术的基本分析框架,这一分析框架基本上包含以下五个步骤:①基于实际问题构造随机模型;②根据随机模型中随机变量的分布产生随机数;③根据随机模型的特点和随机变量的分布假设,选择合适的抽样方法对随机变量进行抽样;④根据随机模型进行仿真试验,求出问题的随机解;⑤对试验结果进行评估。本文将在这一框架内给出一个完整的蒙特卡罗分析框架及其案例演示。
1 蒙特卡罗模拟算法
这里,本文将以经典线性回归模型为例给出蒙特卡罗分析框架。记线性回归模型为:

这里y 是n×1 维被解释变量,x 是n×k 维解释变量,β 是未知的k×1 维参数,ε 为n×1 维残差向量。以上线性回归模通常满足如下假设:
A.2 x 为非随机矩阵,且满足cov(x,ε)=0;
A.3 x 是一列满秩矩阵。
基于以上假设条件,参数β 的最小二乘估计为:

在随机模拟试验中,我们关心的两个统计量评价标准:

基于以上理论模型,我们可以依照以下步骤进行蒙特卡罗试验:
Step 1.设定参数向量β 的真值,选定样本量n;在假设A.1-A.3 下,生成残差向量ε 以及解释变量x;根据式(1)计算解释变量值y。
Step 2.利用式(2)求β 的OLS 估计值;计算模拟标准
Step 3. 重复以上模拟试验(K-1) 次,获得L 个bias(β^ols)和var(β^ols)的估计值,在重复试验过程中,保持n、k、β 以及x 不变。
Step 4.求解蒙特卡罗估计值:
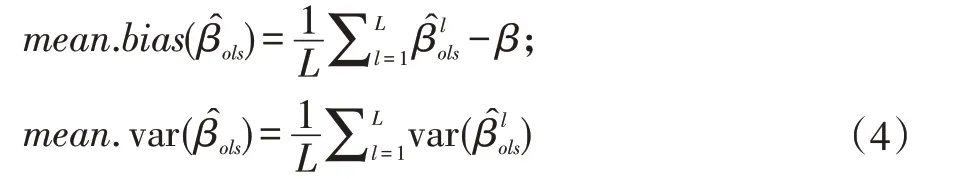
Step 5.对模拟结果进行检查,评估模拟结果和理论是否一致。
2 线性回归模型OLS估计和GLS估计的蒙特卡罗模拟试验
经典的线性回归模型通常假设ε 满足高斯假定,这一假定往往太过于严格,当这一假定不成立时,OLS估计量不再具有有效性,这一结论在理论上易于证明,但确无法通过实证验证。在这一节中,本文将基于蒙特卡罗模拟技术演示当残差项不满足A.1 条件时传统的OLS 估计方法为什么是无效的。为此,我们保持上述A.2 和A.3 不变,A.1 替换为如下A.4:
A.4 εi=ρεi-1+ηi,一阶自相关系数ρ 满足|ρ|<1,残 差 项 ηi满 足 E(ηi)=0 ,E(ηiεi-1)=0 ,以 及
基于以上设定,参数β 的的OLS 和GLS 估计分别为:

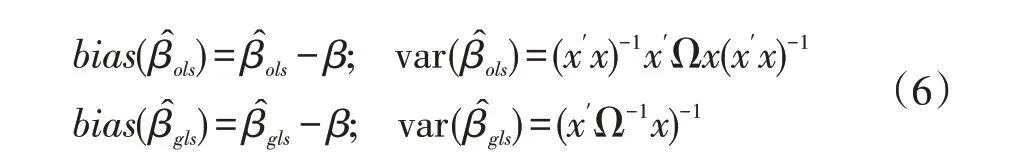
以下模拟过程中,设定β=(1,1)′,n=5,15,30,50,ρ=0.5,0.9 以及=1,5。基于以上蒙特卡罗算法,我们可以给出如表1 的模拟结论。
从表1 可以看出,在所有的模拟设定情况下,GLS估计的方差都小于OLS 估计的方差。此外,OLS 和GLS 估计的方差随着σ2η和ρ 的增大而增大。但是当n增加时,估计的方差减小。而所有估计的偏差值在所有模拟情况下都非常接近于零。

表1
3 结语
蒙特卡罗模拟技术为计量经济学教学提供了丰富的工具资源。在教学过程中,如何教学生有效地构造蒙特卡罗模拟算法是一项非常有挑战性的工作,可以想象,在本科和研究生阶段的课程中,把掌握蒙特卡罗模拟技术作为教学要求的一部分,不仅可以提高学生对理论方法的直观理解,还可以帮助学生掌握一种有效的分析工具。
——基于问卷调查数据分析
——《计量经济学方法论研究》评介

