改进的Hegselmann-Krause舆论演化模型

仝秋娟, 王 欢, 张建科, 李琳娜

(1. 西安邮电大学 理学院， 陕西 西安 710121； 2. 西安邮电大学 陕西省网络数据分析与智能处理重点实验室, 陕西 西安 710121；3. 西安邮电大学 通信与信息工程学院， 陕西 西安 710121； 4. 西安邮电大学 校友办公室， 陕西 西安 710121)

随着信息技术的快速发展，用户可通过微信、微博等社交媒体表达自己的观点与思想。社交媒体具有参与度高、信息发布方便、传播速度快、舆论演化迅速且多样化等特点[1]，已逐渐成为观点的主要源头，同时也影响着大众观点[2]。观点是由于各种事件的刺激，而产生的人们对于该事件所形成的比较一致性的意见倾向[3]。舆论观点是一种强有力的社会控制机制，对社会各方面都将产生深远的影响，网络信息传播及观点的演化是当下关注的一个热点问题。因此，研究观点的形成和演进过程，有助于认识各种观点的本质问题，有助于研究观点背后更深层次的原因及其发展规律，对认识和解释人类某些复杂的行为思想也有着重要意义[4]。

近年来，随着对谣言散播、舆论控制等事件的关注，群体内个体之间的观点交互及其演化过程也逐渐受到国内外学者的广泛关注[5]。通过观点动力学模型[6]，研究社会群体中观点形成、演化以及最终达成共识的过程。观点动力学模型分为离散观点模型和连续观点模型。离散观点模型主要采用有限的离散数值模拟个体的观点，比较典型的有Sznajd模型[7]、投票者模型[8]等；连续观点模型中，具有代表性的是基于有界信任的Deffuant模型[9]和Hegselmann-Krause(H-K)模型[10]。H-K模型中每个个体都有自己的有限置信度，也就是说，每个个体只能与其观点差异值在其置信区间内的个体进行观点交互[11]。对于连续观点的演化问题，H-K模型应用较广泛。利用分数阶非线性系统的观点形成模型，并在该模型中加入领袖观点，可使观点达到共识[12]；通过分数阶H-K领袖观点模型，寻求一种最佳控制策略，使系统最终达成观点共识，并通过数值例子证明了该控制策略的有效性[13]；文献[14]研究了H-K观点形成模型及领袖观点的控制策略，利用数值实验验证了控制策略的有效性以及系统最终达成共识的能力。但是，上述文献均只考虑到人们接受或采纳权威人士或与自身观点相似的观点，忽略了个体对某些话题观点拒绝与排斥的可能性。

在现实生活中，个体对领袖观点的看法介于接受与排斥两个极端心理之间。因此，本文加入非线性领袖观点，同时考虑个体对领袖观点的接受与排斥两类因素，构造非线性耦合函数，建立非线性领袖观点影响的H-K模型，以期研究个体对领袖观点的接受与排斥程度对系统观点达到共识的影响。

1 H-K舆论演化模型

H-K舆论演化模型是将个体观点与周围群体观点进行交互，从而促使整个群体的观点演化，最终形成一致或分散的观点。

1.1 H-K模型

假设系统中个体为N个，在t时刻个体i(1≤i≤N)的观点表示为xi(t)，且观点向量集合x(t)={x1(t),x2(t),…,xN(t)}T∈RN，则H-K模型[12]可表示为

(1)

其中，ξi∈RN为系统给定的初始值。aij=aij[‖xj(t)-xi(t)‖l2]表示个体i与个体j之间观点相互影响的方式。当aij>0时，表示个体j能够影响个体i的观点；否则aij=0。函数fj(·)(j=1,2,…,N)满足Lipschitz条件[12]，即对任意x,y∈RN，满足|fj(x)-fj(y)|≤lj‖x-y‖l2，其中lj是Lipschtz系数且lj>0，‖·‖l2表示欧几里德范数。

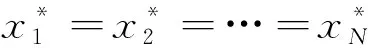
1.2 线性领袖观点影响的H-K模型

为了使所有个体i的观点达到共识，且权威人士的观点较有影响力，在系统(1)的基础上加入领袖观点x0，得到线性领袖观点影响的H-K模型[12]为

(2)

式中，ci=ci[‖xi(t)-x0(t)‖l2]表示领袖与个体之间的影响。当ci>0时，则认为领袖观点能够影响第i个个体的观点；否则ci=0。

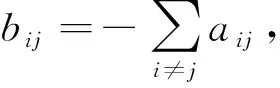
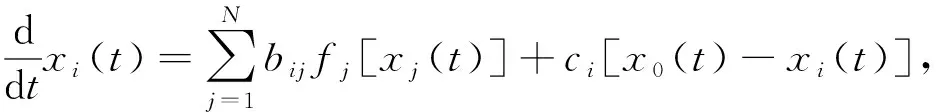
(3)

观点达到共识的定理[12]如下。

定理1 对任意i=1,2,…,N，假设fi(xi)=xi且ci>0，则系统(2)的解将达到共识，即x*=(ξ1,ξ2,…,ξN)T∈RN。

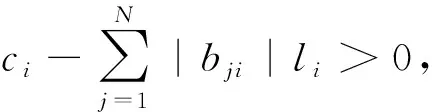
2 改进的H-K模型

综合考虑个体对领袖观点的接受与排斥两类因素，在线性领袖观点影响的H-K模型基础上，将线性领袖观点改进为非线性领袖观点。借鉴观点耦合动力系统[15]，构造非线性耦合函数，建立非线性领袖观点影响的H-K模型。

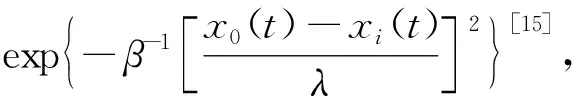
(4)

其中，λ为观点的接受因子，表示个体对领袖观点的接受与采纳程度；β为排斥因子，表示个体对领袖观点的排斥与拒绝程度，β为大于0的实数。

将非线性领袖观点加入系统(1)，得到改进的H-K模型为

(5)

改进的H-K模型利用非线性耦合函数，融合了个体对领袖观点的接受与排斥两类影响，综合考虑了积极与消极的作用。但是，接受和排斥程度不可能同时趋向于无穷，也就是说不存在同时无限接受和无限排斥的双重心理。

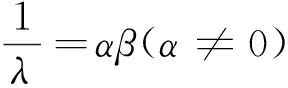
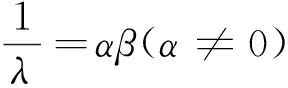
3 实验对比及结果分析

利用Windows7系统的MATLAB 2015a进行模拟仿真。分别以线性、加入噪声以及非线性等3个系统[12]为例，对比H-K模型、线性领袖观点影响的H-K模型和改进的H-K模型的观点演化速度。

3.1 线性系统

当N=4时，线性系统的H-K模型[12]为

(6)

初始条件为x1(0)=1，x2(0)=1.5，x3(0)=2，x4(0)=2.5。系统(6)的观点演化过程如图1所示。

图1 H-K模型观点演化过程

由图1可以看出，当无领袖观点时，由于个体的认知程度各不相同，所以会向与之观点相似的人群靠拢，最终形成几个观点簇，且观点没有达到共识。

在系统(6)的基础上加入线性领袖观点，得到线性领袖观点影响的H-K模型[12]

(7)

初始条件为x0(0)=5，x1(0)=1，x2(0)=1.5，x3(0)=2，x4(0)=2.5。系统(7)的观点演化过程如图2所示。

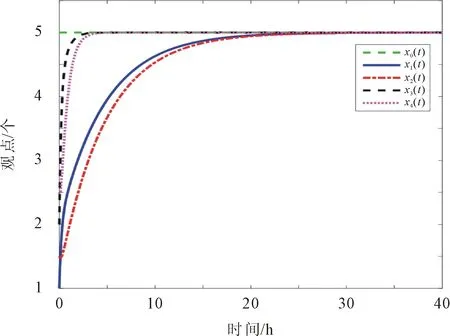
图2 线性领袖观点影响的H-K模型观点演化过程

由图2可以看出，当加入线性领袖意见时，个体倾向于接受权威人士的观点，最终个体的观点趋于领袖观点，使得观点达到共识。

在系统(7)的基础上加入非线性领袖观点，得到非线性领袖观点影响的H-K模型

(8)

初始条件为x0(0)=5，x1(0)=1，x2(0)=1.5，x3(0)=2，x4(0)=2.5。当接受因子λ与排斥因子β取不同值时，系统(8)观点达到共识速度有所不同，演化过程如图3所示。

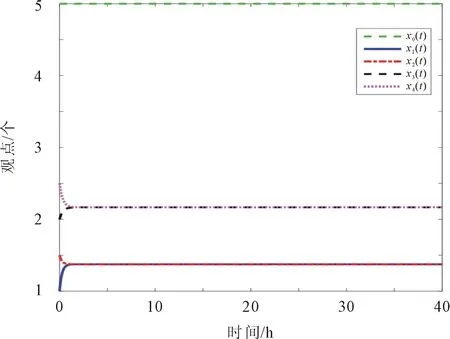
(a) λ=0.38, β=2

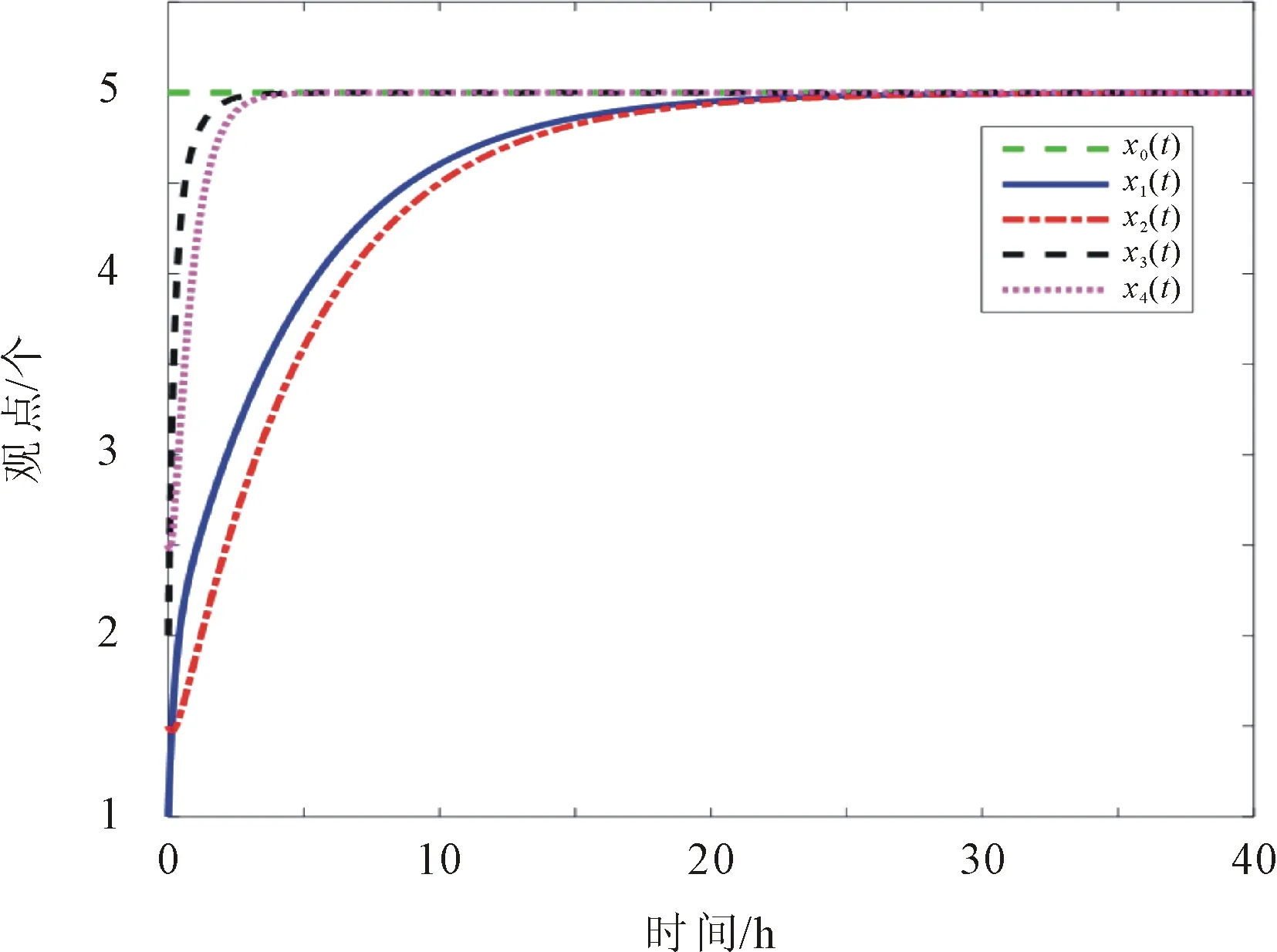
(b) λ=8, β=1

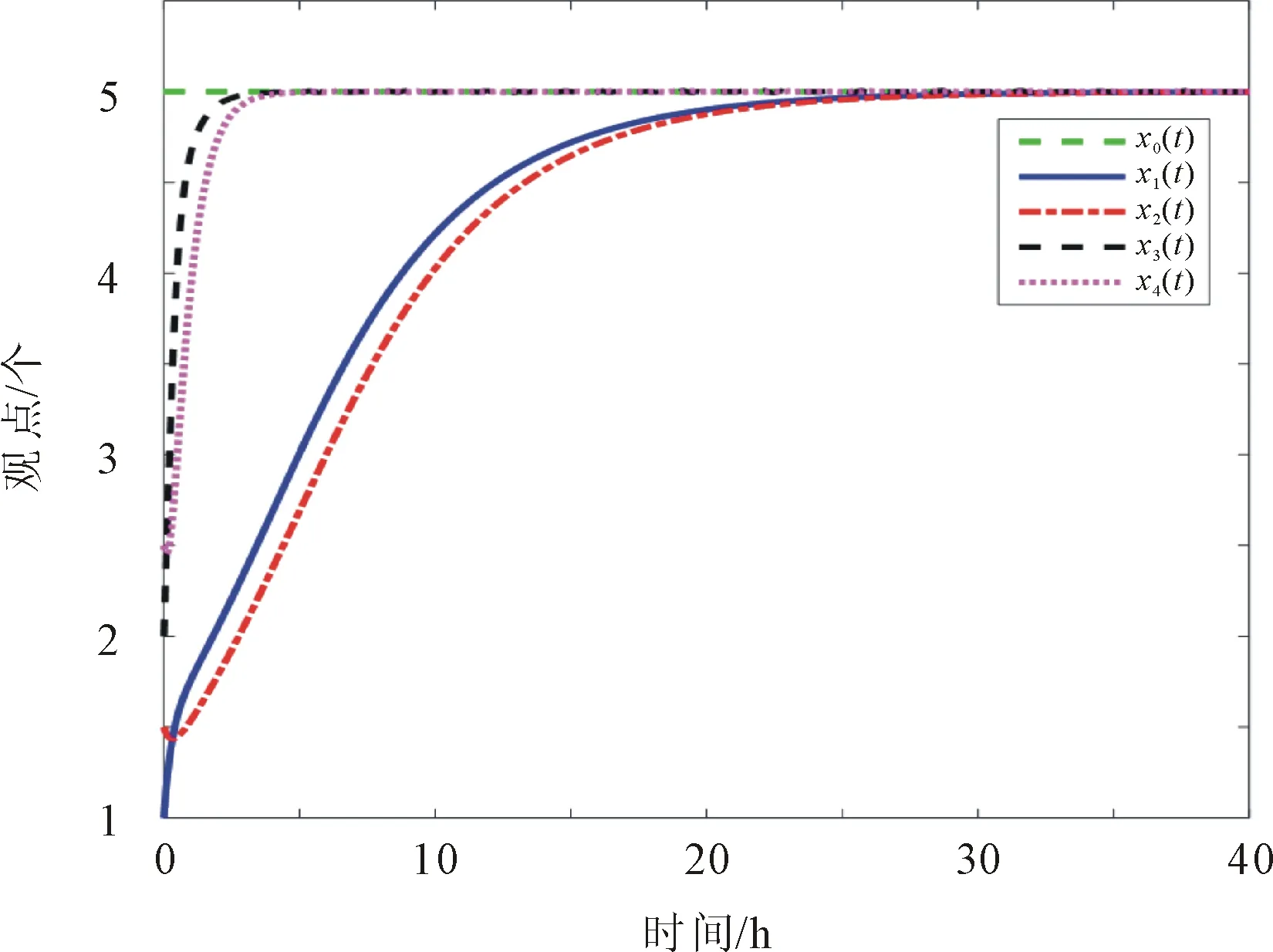
(c) λ=2.1, β=1

由图3(a)可以看出，当接受因子λ=0.38小于排斥因子β=2时，个体对领袖观点持排斥拒绝的态度，则个体坚持自身的观点，观点不能达到共识；当接受因子λ=8大于排斥因子λ=1时，个体对领袖观点持采纳接受的态度，在t=25 h时观点达到一致，如图3(b)所示；当接受因子λ=2.1大于排斥因子β=1，在t=38 h时观点达到一致，如图3(c)所示。由此可知，当接受因子λ与排斥因子β的比值较大时，观点达到共识的用时越短。

3.2 加入噪声后的系统

当N=4时，给线性系统的H-K模型加入噪声，则系统(9)[12]可表示为

(9)

初始条件为x1(0)=1，x2(0)=1.5，x3(0)=2，x4(0)=2.5。系统(9)的观点演化过程如图4所示。

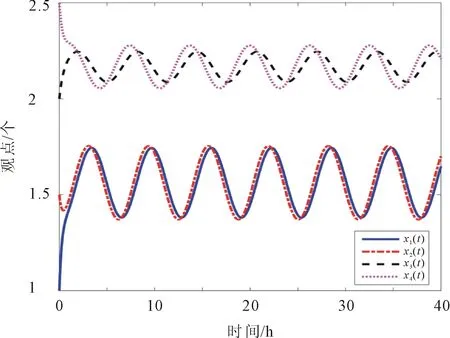
图4 H-K模型观点演化过程

由图4可以看出，无领袖观点影响，个体只与其信任阈值内的个体交流，且只接受与之观点相似或相同的观点，则观点不能达到共识。

在系统(9)的基础上加入线性领袖观点，则线性领袖观点影响的H-K模型[12]为

(10)

初始条件为x0(0)=5,x1(0)=1，x2(0)=1.5，x3(0)=2，x4(0)=2.5。系统(10)的观点演化过程如图5所示。

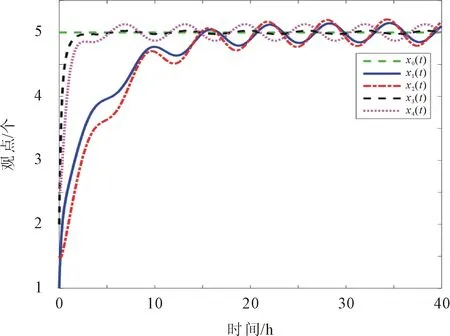
图5 线性领袖观点影响的H-K模型观点演化过程

由图5可知，加入线性领袖观点，个体将接受领袖的观点，最终使观点达到共识。

在系统(10)的基础上加入非线性领袖观点，则非线性领袖观点影响的H-K模型为

(11)

初始条件为x0(0)=5,x1(0)=1，x2(0)=1.5，x3(0)=2，x4(0)=2.5。当接受因子λ与排斥因子β取不同值时，系统(11)观点达到共识速度有所不同，演化过程如图6。

由图6(a)可知，若个体对领袖观点的排斥程度更大，则个体坚持自身的观点，最终不能达到共识；若个体对领袖观点的接受程度大，则观点达到共识，如图6(c)所示，在t=27 h时，观点达到共识；若个体对领袖观点的接受程度远大于排斥程度，则个体的观点更早的达到共识，如图6(b)所示，在t=17 h观点达到共识。

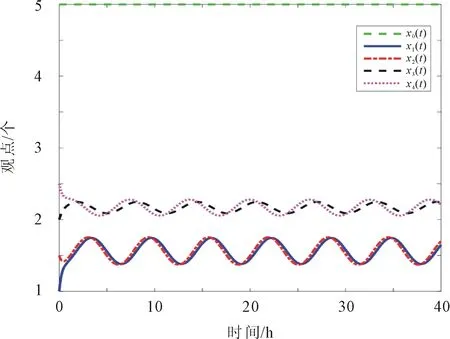
(a) λ=0.38, β=2

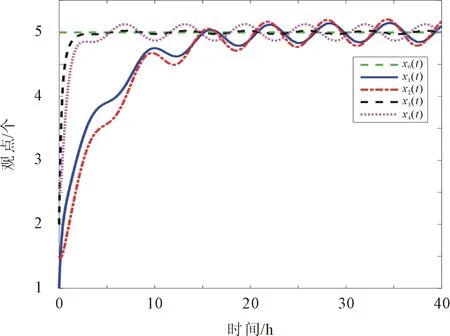
(b) λ=8, β=1

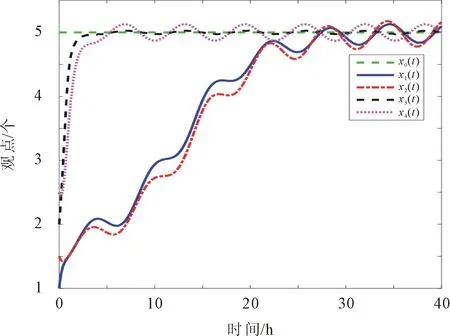
(c) λ=2.1, β=1

3.3 非线性系统

当N=3时，非线性系统的H-K模型[12]为

(12)

初始条件为x1(0)=1，x2(0)=1.5，x3(0)=2。系统(12)的观点演化过程如图7所示。

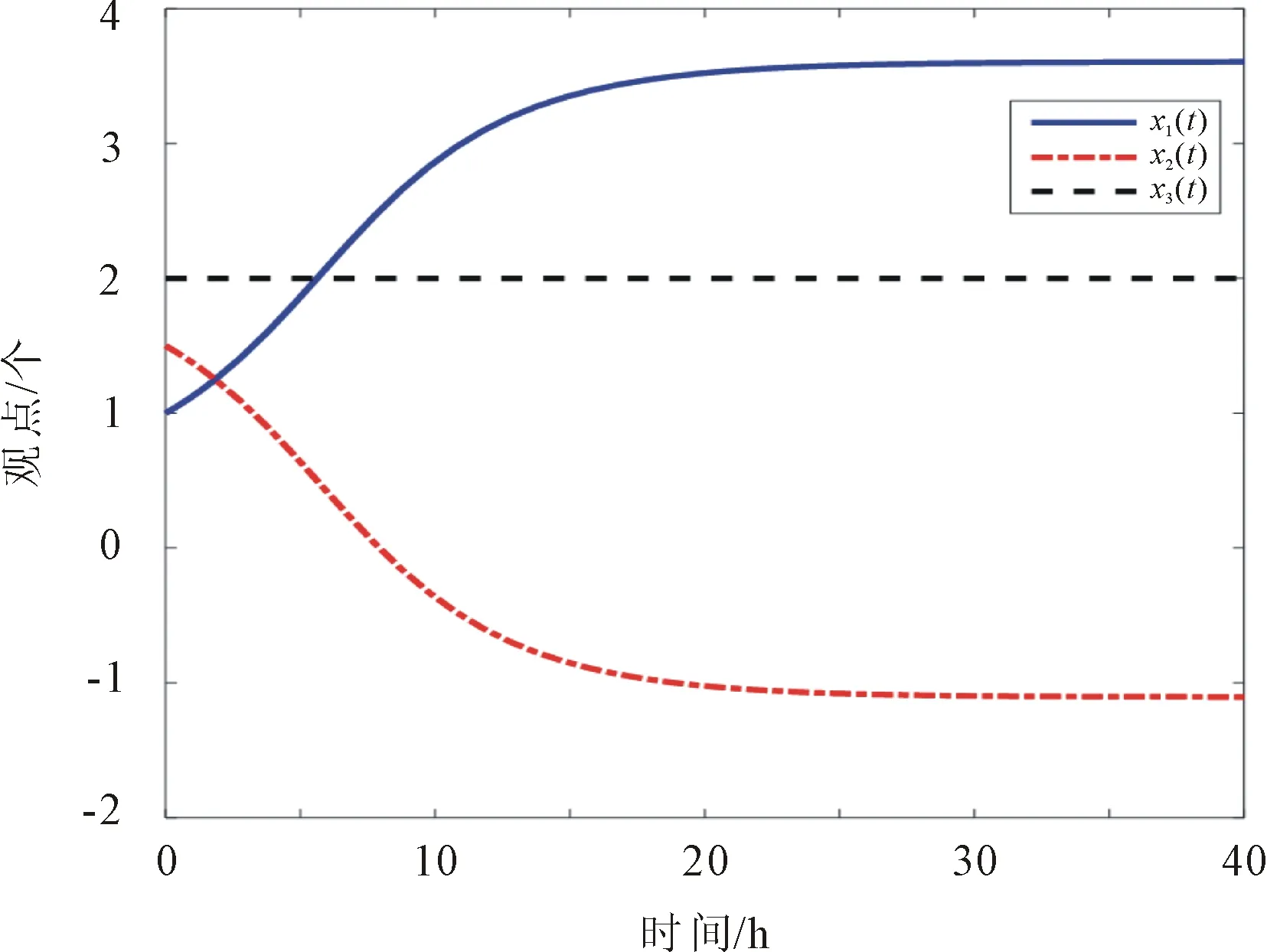
图7 H-K模型观点演化过程

由图7可以看出，当系统中无领袖观点时，个体坚持自身观点或将会向与之观点相似的人群靠拢，最终观点不能达到共识。

在系统(12)的基础上加入线性领袖观点，得到线性领袖观点影响的H-K模型[12]

(13)

初始条件为x0(0)=5,x1(0)=1，x2(0)=1.5，x3(0)=2。系统(13)的观点演化过程如图8所示。

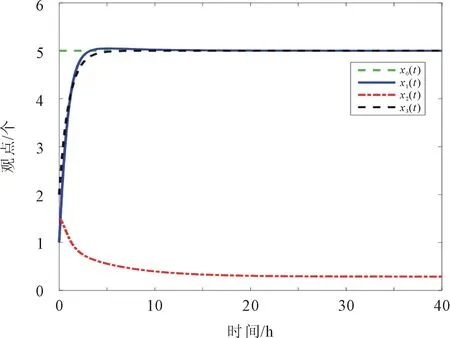
图8 线性领袖观点影响的H-K模型观点演化过程

由图8可以看出，在系统中加入线性领袖观点，个体倾向于接受领袖的观点，最终系统的观点达到共识。

在系统(13)的基础上加入非线性领袖观点，得到非线性领袖观点影响的H-K模型

(14)

初始条件为x0(0)=5,x1(0)=1，x2(0)=1.5，x3(0)=2。接受因子λ与排斥因子β取不同值，系统(14)观点达到共识速度有所不同，演化过程如图9所示。

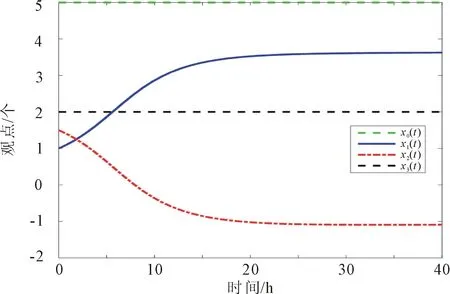
(a) λ=0.38, β=2

(b) λ=8, β=1

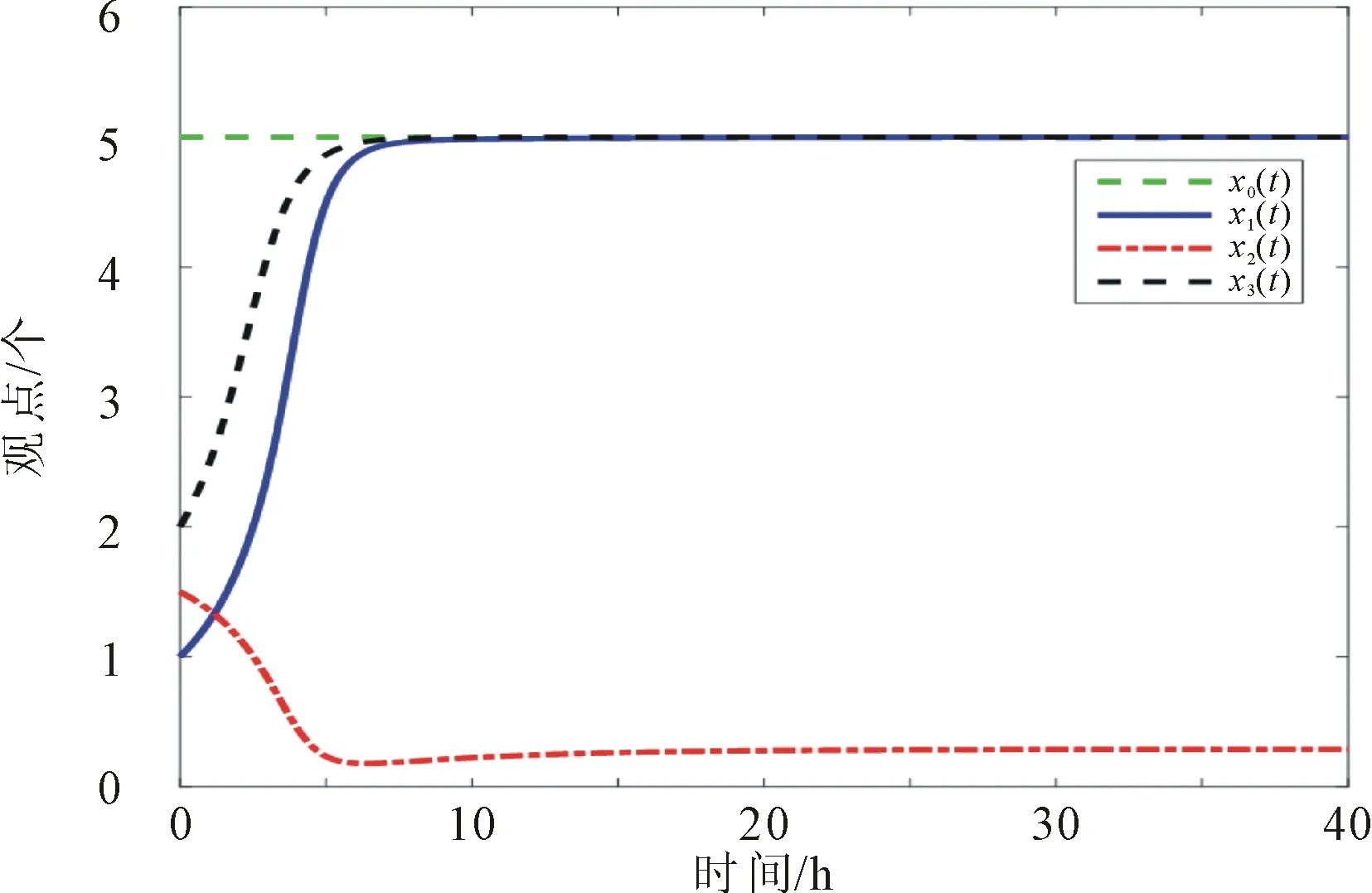
(c) λ=2.1, β=1

由图9可见，加入非线性领袖观点的系统，当个体对领袖观点的接受程度比排斥程度大时，最终观点达到共识。当接受因子λ=8远大于排斥因子β=1时，观点在t=4 h时达到共识；在接受因子λ=2.1大于排斥因子β=1时，观点在t=7 h达到共识，由此可得，当接受因子远大于排斥因子时，观点达到共识的时间越短。

4 结语

在考虑了个体对领袖观点的接受与排斥两种因素情况下，研究了非线性领袖观点影响的H-K模型演化过程。利用非线性耦合函数融合了接受因子λ与排斥因子β，通过接受因子λ与排斥因子β的大小判断系统的观点是否达到共识。仿真结果表明，H-K模型中的个体只能与其信任阈值内的个体进行观点交互，所以当系统中无领袖观点时，最终观点不能达到共识；当系统中加入线性领袖观点时，个体倾向于接受领袖的观点，最终使观点达到共识；而改进的H-K模型，加入了非线性领袖观点，若个体对领袖观点的接受程度大于排斥程度，则个体倾向于接受领袖观点，最终观点达到共识，且当个体对领袖观点的接受程度比排斥程度更大时，观点达到共识的时间更短。若个体对领袖观点的排斥程度大于接受程度时，则个体对领袖观点持有排斥的态度，最终观点不能达到共识。