渡槽结构运行状态监测技术研究进展

张建伟，张天恒，华薇薇

(1.华北水利水电大学，河南 郑州 450046；2.水资源高效利用与保障工程河南省协同创新中心， 河南 郑州 450046；3.河南省水工结构安全工程技术研究中心， 河南 郑州 450046)

渡槽作为一种跨越式的空间薄壁输水建筑物，广泛应用于农业灌溉工程和其他大型水利工程中，为缓解水资源时空分布不均这一问题发挥着积极作用[1]。渡槽在实际运行期间，由于环境因素及槽内水体作用的影响，会造成渡槽结构不同程度的破坏，甚至危及结构安全[2]。渡槽结构易产生表层混凝土剥蚀、蜂窝、钢筋外露、裂缝、渗漏、地基不均匀沉降、材料老化、整体或局部失稳、倒塌等病害症状[3-4]。对渡槽运行状态进行科学的监测有助于发现结构的早期病害，进行及时维护与加固，保证渡槽的结构性能，避免灾难性事故的发生。为保障渡槽结构的安全运行，笔者从振测传感器的优化布置、特征信息提取、多测点信息融合与运行状态监测等视角，阐述了渡槽结构运行监测技术的研究进展。

1 传感器优化布置

传感器的优化布置，即在结构关键位置布设有限数量的传感器，进而从被噪声污染的信号中获取到最有价值的振动信息。传感器的布设是个优化组合问题，优化方法的选择直接关系到计算的效率和结果的可靠性，当前已提出了诸多测点优化方法，大致分类如下。

1.1 传统的优化算法

传统的传感器优化方法包括有效独立法、QR分解法、模态置信准则及能量法等。当前应用最广泛的优化方法是有效独立法[5]，其本质是保留对模态向量线性无关贡献最大的测点，通过有限的传感器获得更多的模态信息，得到对模态的最佳估计。何龙军等[6]基于修正后的距离系数-有效独立法，有效缓解了大型空间结构测点之间的信息赘余问题。袁爱民等[7]结合MAC准则和有效独立法的优点，保障了桥梁信息向量的正交性和线性无关性。刘伟等[8]考虑了截断模态线性独立的同时，选择含有较高模态动能的测点，提出了具有较强抗噪能力的有效独立-模态动能法。李火坤等[9]提出基于QR分解和MAC准则的高拱坝传感器优化布置方法，结果表明该方法识别精度高。张建伟等[10]针对有效独立法布设测点能量较小的缺陷，提出基于有效独立-总位移法的传感器优化方法，将测点的总位移按权重的大小加入优化过程中，同时保留有效独立法的优点，最终得到独立性较好且满足能量要求的测点信息。

1.2 智能优化算法

智能优化算法主要包括遗传算法、神经网络法、模拟退火算法和蚁群算法等，此类算法具有较好的并行性和搜索全局性，但依然存在缺点，例如，迭代次数多、收敛速度慢。刘娟[11]提出了二重结构编码的遗传算法，证明了全局寻优遗传算法的优越性。高维成等[12]基于QR分解来提高收敛速度，并采用遗传算法中的强制变异规则避免测点重叠。Kirkpatrick等[13]利用模拟退火算法对传感器优化布置，并取得较好的效果。这些智能算法相较于传统算法思想更为变通，力求全局最优值，然而其稳定性和搜索能力仍存在不足。

渡槽监测系统中传感器的主要任务是为渡槽损伤识别和状态评估系统提供可靠的响应数据。传统和单一的优化方法仍存在不足，这些算法还亟待进一步改善。

(1) 将单一的优化理论优势互补形成新的结合算法，使其兼备两者的优点。例如将有效独立法和模态保证准则结合获得线性无关和正交的信号，正是两种算法优点结合的体现。

(2) 实践研究表明，在结构损伤过程中应力、应变信息比位移更加敏感，应重视传感器在应力、应变信息采集方面的研究，应力、应变传感器在传感器优化方面具有广阔的前景。

2 振动特征信息提取

由于渡槽工作条件的复杂性，导致外界环境激励引发的噪声信号(水流脉动、大地脉动)融入结构真实信息，测试信号中的大量干扰噪声很大程度上掩盖了结构真实的振动特征信息，导致结构安全评价存在偏差。因此，为提高结构安全监测精度，需对实测信号滤除干扰噪声，提取反映结构特征的真实信息。

传统的特征信息提取方法如数字滤波、小波阈值[14]等在各个领域取得了较好的效果，理论和技术都已经很成熟，但均存在很大的局限性。数字滤波在数据长度较短时易造成信号的失真变形，滤波精度较低。小波阈值的降噪效果过度依赖小波基和阈值函数，且该方法在分析信号的过程中不具有自适应分解特性。奇异值分解(Singular Value Decomposition，SVD)降噪对高频噪声具有较强的滤波能力，当处理低频噪声时，其滤波能力将会大幅度地降低。近年来，经验模态分解(Empirical Mode Decomposition，EMD)[15]、集合经验模态分解[16](Ensemble Empirical Mode Decomposition，EEMD)以及经验小波变换[17](Empirical Wavelet Transform，EWT)等新型的特征信息提取技术被提出，并应用于各个领域。

2.1 经验模态分解

经验模态分解(Empirical Mode Decomposition，EMD)是由Huang等[18]提出的一种适用于处理非线性非平稳信号的时频分析方法，该方法根据信号的尺度特征自适应分解成一系列从高频到低频的物理意义不尽相同的固态模量(Intrinsic Mode Function，IMF)，此方法已在多个领域信号研究中应用，具有很高的时频分辨率。EMD分解流程如图1所示。EMD方法克服了小波分析等信号处理方法依赖主观经验的缺点，其不需要提前设定基函数，然而由于其计算理论的缺陷，在分解过程中容易出现模态混叠现象[19]。

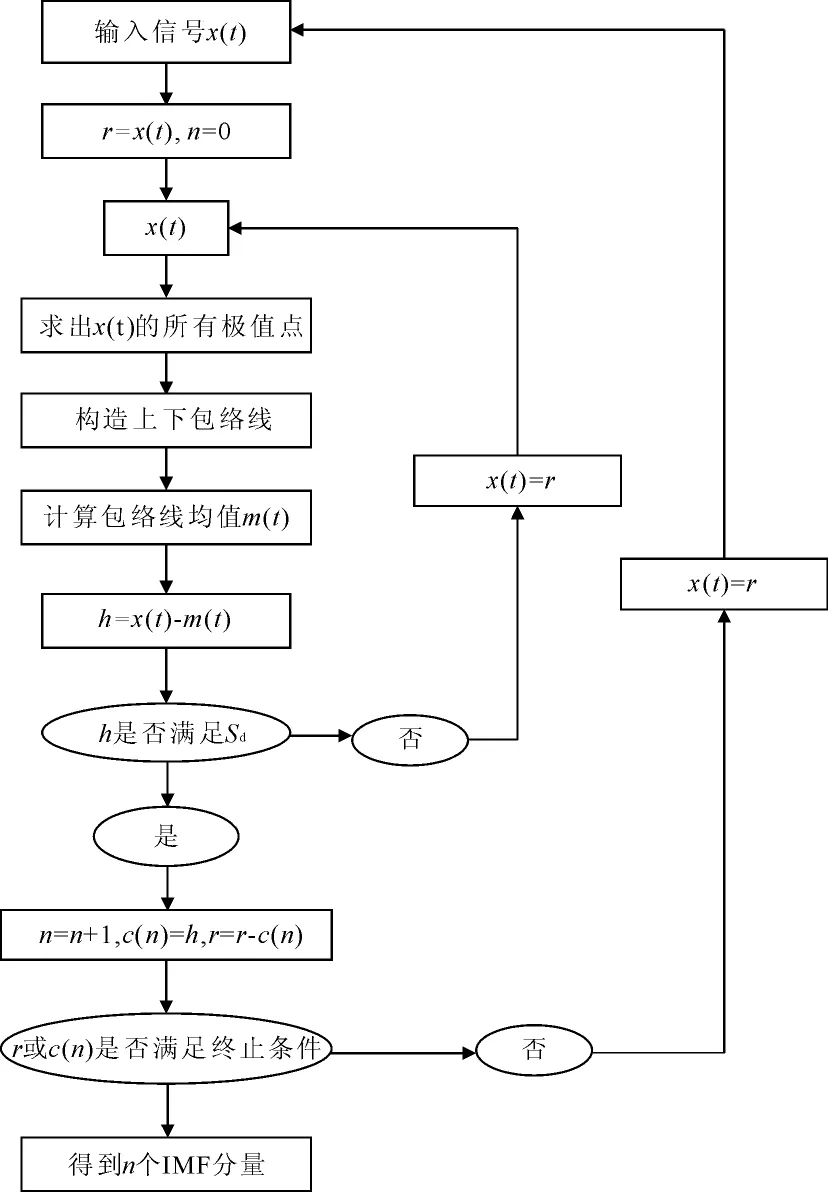
图1 EMD分解流程图

2.2 集合经验模态分解

集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)首先需要多次对原始信号x(t)中施加白噪声，进而对其进行EMD分解，然后将多次EMD分解获得的各IMF分量进行平均得到最终的IMF分量，该方法是对EMD方法的改进，可以一定程度上改善模态混叠现象[20]。

EEMD算法试图通过多次集成平均来抵消白噪声对分解结果的影响，但并不能完全消除；其重构误差的大小过度依赖集成次数，虽然可以通过增加集成次数来减少重构误差，但该过程无疑会增长计算耗时，严重影响计算效率。

2.3 经验小波变换

经验小波变换(Empirical Wavelet Transform，EWT)由Gilles[21]提出，该方法综合了EMD和小波的优点，同时又克服了小波不能自适应分解的缺点，其计算量远小于EMD和EEMD。EWT的基本原理为：根据原信号的频谱特征将其分割为多个区间，每个区间中具有不同的带通滤波器，通过对原信号进行滤波处理，提取出各个调幅-调频分量，将信号自适应地分解。EWT的主要步骤如图2所示。

图2 EWT方法实现流程

EWT虽然优于EMD及EEMD等方法，但该方法需要人为设定分解层数，并且抗噪性差，强背景噪声会大幅度降低其模态分量提取精度[22]。

2.4 变分模态分解及其改进算法

虽然EMD、EEMD及EWT等新型滤波方法明显优于传统方法，但都有各自的缺点。EEMD工作量庞大，计算效率低。EWT在噪声成分低时滤波精度较高，但噪声含量过大时其滤波精度大幅度地降低。变分模态分解[23](Variational Mode Decomposition，VMD)是近年来新提出的方法，与EMD、EWT等方法相比，VMD的分解过程收敛速度更快，计算精度更高。

VMD是多分量信号自适应分解的新方法，该方法通过构造及求解变分问题，确定每个IMF分量，从而实现信号的有效分离。马增强等[24]通过构造含噪声的仿真信号，采用变分模态分解与奇异值分解联合的方法进行降噪，结果表明该方法可有效的消除噪声影响。付文龙等[25]提出基于增强VMD相关分析的摆度信号降噪方法，通过仿真分析与实测信号降噪验证，证明了该方法具有较好的降噪性能。

VMD算法中模态数K的确定至关重要[26]。K值的选取极大影响结果的准确性，若K值太大会导致过分解，K值太小时部分IMF不能被有效识别。Dragomiretskiy等通过判断各个模态之间是否正交或者频谱是否重叠确定K的取值，但该方法很难实施。Wang等[27]利用VMD检测转子系统的碰磨故障，并通过数值仿真验证VMD算法在多特征提取方面较EWT、EMD和EEMD优越，但是其K的取值是根据经验进行选取的。唐贵基等[28]利用PSO算法自动确定K的取值，但该方法的优化结果依赖于适应度函数和各项参数的设置，如果参数选择不当，将无法保证分解结果的准确性。为此，张建伟等[29]提出了利用互信息法自适应地确定K值的IVMD方法，克服VMD盲目选取分解参数的缺点。

2.5 IVMD-SVD联合滤波

IVMD基于模态特征和互信息准则能够自动确定模态数，有效克服VMD盲目选取参数的缺点。此外，IVMD具有较强的抗噪能力，能够去除低频及部分高频噪声，与EMD、EEMD等方法相比，IVMD收敛快、计算效率高、鲁棒性强。但是IVMD对部分高频噪声的滤波能力有限，可能会造成部分高频噪声的残余，最终影响结构安全监测精度。因此，对IVMD滤波后的信号进一步处理，滤除残余的高频噪声至关重要，有利于进一步提高滤波精度。

SVD降噪作为一种经典的正交化分解降噪方法，对信号中的高频随机噪声具有很强滤除能力。因此，本文充分结合IVMD和SVD的特点，提出了IVMD-SVD联合降噪方法。该方法可去除干扰噪声，提取结构的真实振动特性。IVMD-SVD联合滤波流程如图3所示。

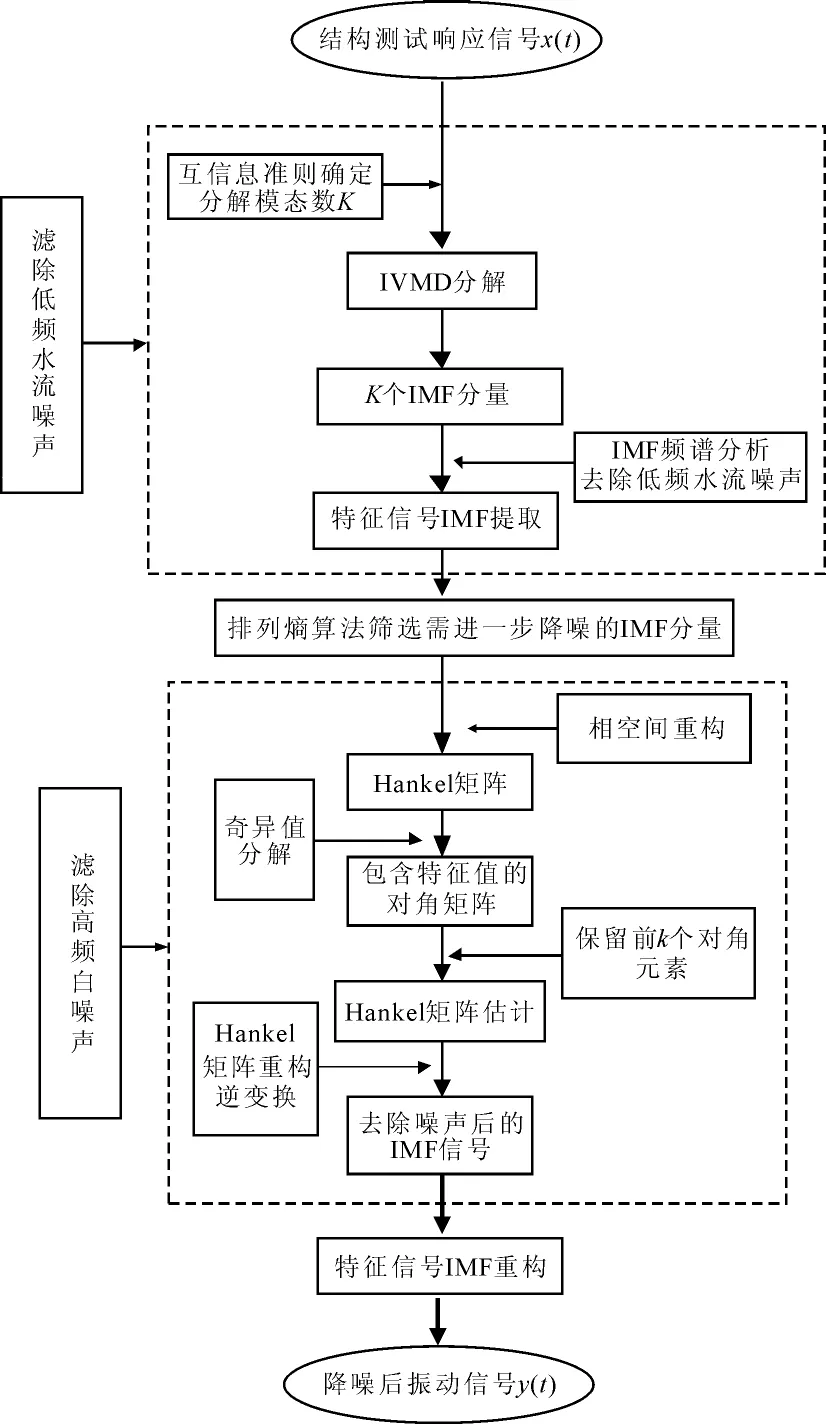
图3 IVMD-SVD联合滤波流程

以某渡槽为例，采用IVMD-SVD方法对采集到的振动信号进行降噪，为验证该方法的有效性，同时采用IVMD与SVD方法对渡槽振动信号分别进行处理，并进行对比分析，如图4所示。

分析可知，IVMD-SVD方法不仅能够滤除噪声干扰，而且能更好的保留结构真实有效信息，对渡槽结构振动特征信息提取具有较好的实用性。

3 多测点信息融合

信息融合是指将结构的局部数据信息，通过一定的组合方式，得到一组更真实反应结构整体振动特性的新数据。结构的多测点信息融合，相当于利用传感器采集到的信号对同一结构的不同部位以及不同方面的特征信息进行融合。不同测点信息之间的关联性不同，不同测点含噪声成分比重也不同，有效特征信息所占的比例也不同。此外，不同测点的

图4 3种方法处理效果对比图

测试信号提取的特征频率也可能不同，但有一些互补信息。基于多元信息融合的渡槽结构安全运行监测研究，避免了常规的采用单一静态监测仪器进行“点”监测的缺点，而对各静态、动态监测效应量信息进行多级融合，可以更全面地反映渡槽结构整体的安全状态。

信息融合按照融合程度的高低可以分为三类。数据级融合是将获得的信息直接融合，精度最高，但计算量较大。特征级先提取信息的特征，再将特征进行融合，数据量减小，但精度有所降低。决策级融合是将各种子决策进行融合，其层次最高，误判风险低。

3.1 数据级信息融合

数据级融合方法具有精度高、数据损失少、细微信息丰富等优点，但也有一些缺点，例如计算时间长、代价高、要求同类传感器、容易受外界干扰等。由于精度较高，数据级融合应用较多。Ren等[30]首次将一致性融合算法应用于多传感器测试数据的融合，并验证了方法的可行性。李学军等[31]提出了可自动筛选有效信息的方法(即互相关融合方法)，该方法能够准确识别失效的传感器，提高信息融合的精度。Zhang等[32]和李火坤等[33]提出了基于方差贡献率的多测点信息融合方法，可有效将多测点监测数据融合为反映结构整体特性的信号。随着渡槽整体结构的复杂化，其安全监测问题愈受关注。单一传感器只能反映结构局部特征，基于方差贡献率的数据级信息融合方法能在动态融合模式下兼顾传感器信号间的冗余性、互补性及相关性，使信号更真实反映渡槽整体振动特性[34]。

3.2 特征级信息融合

特征级信息融合的核心是先提取信息的特征，再将特征进行融合。该融合算法对数据进行了有效地压缩，计算效率提高，但部分有效信息损失，融合精度有所降低。特征级融合算法主要包括Kalman滤波、人工神经网络等。例如郭张军等[35]将Kalman滤波融合算法用于大坝坝基水平位移计算和分析，克服了单个监测点得到的计算结果不一致的问题，工程实用性较强。

3.3 决策级信息融合

决策级融合层次最高，该方法先对单一测试信息进行判断，从而得到多个子决策，最后将各种子决策融合得到总决策。由于数据量少，因此其精度与其他两种融合方法相比较低，但是它计算成本低、可用于异类传感器。决策级融合算法有Bayes推理、模糊积分、D-S证据理论等。例如叶伟等[36]用将加权优化的D-S证据理论方法应用于西溪大坝的安全评价，取得较好结果。He等[37]将Bayes理论用于大坝多测点融合中，为大坝的状态评价和异常诊断奠定基础。

单点监测有效反映了监测点所处的局部行为，无法准确反映渡槽的整体结构行为。综上所述，信息融合的研究已成为热点和发展的主要方向，它有机连接多个监测点的监测数据，有效克服单点监测分析和建模分析的局限性。目前，多传感器信息融合技术日趋成熟，将信息融合技术应用于渡槽结构安全监测，对掌握渡槽整体结构性能具有实际意义。

4 渡槽结构在线运行监测

4.1 传统运行状态监测参数

通过振动测试对结构运行状态进行识别和判断应用较多，其成本低、易于操作。通过分析测试数据，获取能够反映结构振动特性的重要参数。参数的取值可有效反映结构的不同状态。应用较多的状态识别参数主要包括：固有频率、应变、振型等。

固有频率出现的时间较早，是结构重要的模态参数。固有频率的操作简单，根据频率的变化即可判断结构的运行状态，如Penny等[38]根据频率的变化识别结构的不同状况，并且利用数值仿真方法设置了三种运行工况，不同运行工况下频率的变化量不同，印证了利用频率进行运行状态识别的可行性。不同运行工况可能得到相同的频率变化量，当结构运行状态变化较小时，频率的识别结果也不明显。

与固有频率相比，振型对结构运行状态的识别较准确，但结构振型的提取较麻烦。沈文浩等[39]利用MAC和COMAC指标识别悬臂梁结构的损伤，结果表明这两个指标均能较好地识别结构的运行状态，与MAC相比，COMAC的计算过程更繁琐，需要更多阶次的模态。振型指标用于模型的损伤识别精度较高，但对于实际的工程来说，该方法局限性较大。

应变是比位移对损伤更敏感的灵敏指标，且根据应变变化可实现对结构的损伤定位。范涛等[40]利用数值仿真说明了应变对结构的损伤位置和程度较敏感，并将分析结果与位移模态进行了对比，说明了应变模态的优越性。

除此之外，刚度在结构发生变化时也会随之改变，但研究表明刚度对结构初期变化识别不敏感，适用于结构发生较大变化的情况。

4.2 运行状态动态监测参数

频率、振型、应变等局部监测指标用于模型试验能够很好的识别结构状态，但对于运行条件较复杂的过流结构灵敏度较低，并且过流结构的振动信号含有大量的水流噪声及高频白噪声等背景噪声，上述指标的抗噪性能差，会严重影响最终的判断结果。

排列熵(Permutation Entropy，PE)由Bandt等[41]提出，与其他常用的方法相比具有计算效率高、抗噪性强、易于在线监测等特点，然而，PE忽略了相同时间序模式之间的幅度差异，且丢失了关于信号幅值的信息。多尺度排列熵(Multiscale Permutation Entropy，MPE)和加权多尺度排列熵(Weighted Multiscale Permutation Entropy,WMPE)通过结合幅值信息来弥补PE在尺度上的限制[42]。WMPE通常表现出规律性或在不同时间尺度上受到噪声影响的片段权重分配的复杂性，对结构运行状态监测具有一定优势。MPE和WMPE适用于单通道时间序列的复杂性分析，单个通道单独分析会导致跨通道关联性的信息丢失，对于渡槽结构整体安全监测，需对各通道的运行状态进行融合分析。多通道加权多尺度排列熵(Multivariate Weighted Multiscale Permutation Entropy，MWMPE)本质是对不同时间尺度多通道信号的复杂性分析，MWMPE不仅可以准确测量多通道数据的复杂性，还可以反映多变量时间序列中包含的更多信息，并且具有更好的鲁棒性。因此，与WMPE方法相比，MWMPE可以直接分析多通道数据，同时，它可以严格统一地处理数据通道的不同嵌入维数，时间滞后和幅度范围。

在某渡槽结构上布置6个测点，共14个通道。采用MWMPE方法对不同水位情况下的监测数据进行计算分析。如图5所示，MWMPE方法将多通道信号融合为一条反映结构运行状态的熵值曲线，并能准确反映结构运行状态的变化情况。随着水位的升高MWMPE值变小，在水位变化节点处，熵值表现出明显的突变，当水位趋于稳定时，熵值也逐渐平稳。

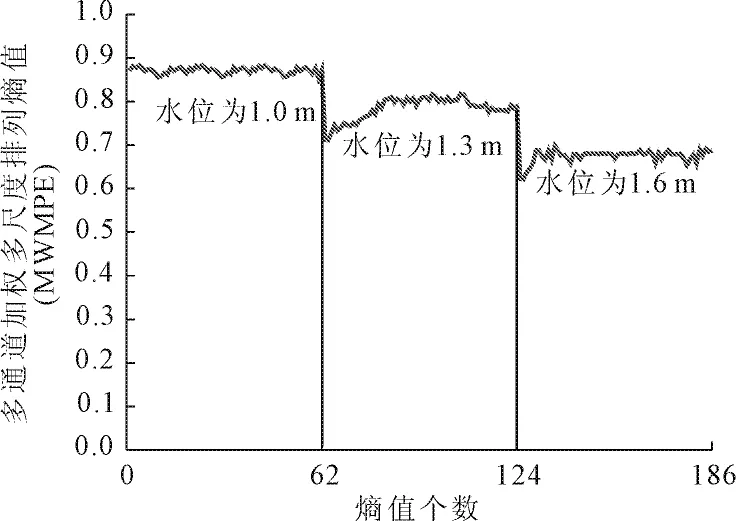
图5不同水位下MWMPE值

当水位越低时，水的流速越大，监测信号复杂性越高，所以熵值也越大，在水位变化节点处，水流对渡槽结构的影响达到最大，使得熵值发生突变，当水位趋于稳定时，振动信号的复杂性表现出同一水平，熵值曲线也随之平稳。因此，MWMPE方法融合后的熵值变化曲线可反映结构的运行状态。

综上所述，熵值可有效的分析渡槽结构的运行状态，它能够捕捉时间序列的不确定性与无序性而不对理论概率分布施加约束。随着结构运行状态的变化，熵值也随之改变，熵值变化量的大小反映结构运行状态的变化程度。因此，熵值是对渡槽结构运行状态识别的敏感性动态指标，MWMPE可以直接分析多通道数据，更加全面的反映渡槽结构整体的运行状态。

5 结 论

(1) 渡槽结构的状态监测研究具有重要的现实意义，有助于发现渡槽结构的早期病害，及时维护与加固，确保渡槽结构安全运行，使其发挥最大效益。

(2) 针对渡槽结构的工作特点，本文从振测传感器优化布置、特征信息提取技术、多测点信息融合技术、敏感指标在线安全监测技术等方面，对渡槽结构的状态监测研究进展进行总结与评述。