基于弹性绳算法的无人机路径规划方法

田景凡 王彦恺

（北京理工大学宇航学院，北京 100081）

1 引言

无人机路径规划是无人机任务设计与规划的重要环节，是实现无人机自主飞行与任务执行的重要阶段。路径规划问题是指在已知环境信息的任务场景中，预先规划出从各个无人机起始点到对应目标点，可以绕过途中各种威胁区和障碍物，安全、可靠、无相互碰撞，且同时满足无人机自身约束条件的可飞行路径，是任务规划系统研究的难点之一。

一般情况下，无人机任务路径规划需要满足的原则如下：（1）任务规划应该得到一条从任务起点到任务终点的路径，不能存在规划失败。（2）无人机在向目标运动的过程中需要保证安全，不碰到障碍物或者经过危险区域。（3）规划的路径应尽量优化，满足规划阶段对路径长度的要求。

无人机路径规划的实现主要包括以下两个步骤：（1）环境建模。根据无人机所处的实际环境，在仿真过程中建立合理的模型，将实际的物理空间抽象成为能用数学模型求解的虚拟空间。（2）路径搜索。在完成环境建模之后，根据任务条件规划出一条从起点到终点的任务路径，在满足任务条件约束的同时使路径长度最短。

无人机路径规划问题一直是国内外学者研究的热点问题。二维空间路径规划的研究方法很多，包括A*算法、人工势场法、进化算法、蚁群算法和粒子群优化等。至于三维空间，情况会变得更加复杂，二维空间中的许多算法不能直接应用于三维空间。三维空间中常用的路径规划算法包括稀疏A*算法、快速随机树法和弹性绳算法等。

不同文章中对弹性绳的定义和计算方法有所不同，但本质上都是通过弹性绳来优化和选择路径的。本文将弹性绳定义为连接起点和目标点的一组节点，通过节点与障碍物的碰撞和滑动，可以得到空间中最短的路径。利用串联的弹簧组成弹性带的方法建立连接车辆和目标点的行驶路径，弹性带在弹力平衡的作用下引导车辆的避障和超车行为，就是典型的弹性绳算法。

2 无人机路径规划框架

无人机路径规划问题需要综合考虑地形、威胁等因素，结合无人机自身飞行性能，规划出从起点到终点的最优飞行路径。假设无人机i在三维空间中的位置为Pi，则无人机路径的一组节点序列为{Si,Pi1,Pi2,…,Pij,…,Ti}，i∈ [1,N]，其中 Si为起始点，Ti为目标点。

在无人机路径规划问题中，应考虑无人机在三维空间中的运动，假设无人机为空间中的一个质点，将无人机的运动学模型简化为：

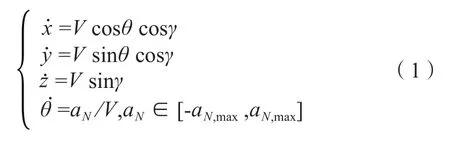
式中，(x,y,z)为无人机的空间位置；θ为无人机的航向角；γ为无人机的俯仰角；aN为无人机的法向加速度；V为无人机速度且为定值。

3 无人机路径规划算法设计

弹性绳算法是通过对弹性绳收缩运动的简化模拟，利用算法的收缩特性对三维空间中的路径进行规划的方法。弹性绳在空间中的运动过程可以描述为在拉伸状态下固定一根弹性绳的两端，弹性绳在弹性力作用下收缩，最后收缩到长度最短的状态。如果空间中存在障碍物，弹性绳将会沿着障碍物表面滑动并收缩到空间中长度最短的状态。

在空间中的三维点集S={P1,P2,…,Pn}(n≥3)，该点集S中相邻两点相互吸引，且力的大小与两个节点之间的距离有关，距离越大则吸引作用越强，将该点集S称为弹性绳系统。弹性绳系统的示意图如图1所示。

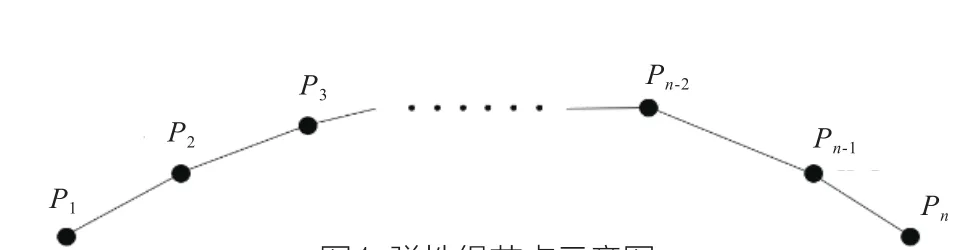
图1 弹性绳节点示意图

弹性绳的运动过程可以分为4种状态，分别为收缩、碰撞、滑动和平衡。根据弹性绳系统的定义，弹性绳可以看做由n-1段原长为零的弹簧相互连接而成，每段弹簧的能量与弹簧伸长量的平方成正比，弹性绳系统的总能量为每段弹簧的能量之和，即

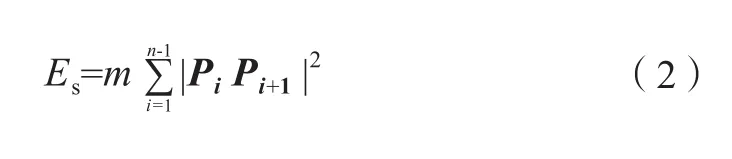
根据中线定理2(|AB|2+|AC|2)=|AB+AC|2+|AB-AC|2(其中A、B、C是空间中任意不共线的三点)可知，当弹性绳发生收缩、碰撞或滑动时，均会产生总能量的降低。根据能量的定义可知，Es≥0，即弹性绳系统总能量存在下界。根据系统能量单调递减且存在下界可知，系统能量存在极限Es*，即弹性绳系统可以收敛到空间最短状态。弹性绳系统中的节点在相互作用下可以收缩到系统势能最低的状态，此时弹性绳的长度达到空间最短状态。

弹性绳S={P1, P2,…, Pn}（n≥3）的各个节点在相互作用下逐点运动，经过一轮运动后变为S'={P'1,P'2,…, P'n}（n≥3）。对于弹性绳上任意一点Pi(i=2,3,…,n-1)，其运动分析如图2所示。

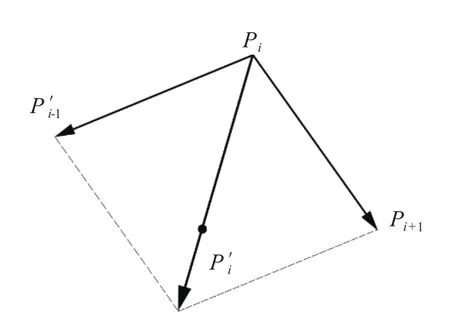
图2 运动分析示意图

假设在节点Pi运动时，其相邻点P'i-1和Pi+1固定，节点Pi受到相邻点的吸引作用，合力方向为PiP'i-1+PiPi+1。由此可得弹性绳节点的收缩位置计算公式为：

式中，Si为点Pi的位移矢量(i=2,3,…,n-1)；k∈(0,1)为比例系数。

弹性绳算法和大多数优化算法一样，在运算过程中也可能会遇到局部最优的问题。通过算法的运算过程可以知道，弹性绳算法通过节点收缩完成最优路径规划，是一种局部寻优的算法。组成弹性绳的某一节点的运动和位置更新只由该节点的相邻两节点确定，节点更新和位置选择模式单一，缺少对空间中最优位置的搜索能力。在节点收缩及沿障碍物表面滑动的过程中，如果组成弹性绳的节点偏离了整体最优解的运动方向而朝着局部最优解的方向运动，结果就是弹性绳算法在后续运算中将会朝着局部最优的方向继续收缩而无法跳出，从而出现陷入局部最优解的情况。

由式（3）可知，组成路径的弹性绳节点在算法运算过程中的运动方向和更新后的位置仅由与该节点相邻的两节点确定。算法在收缩过程中由于缺少对收缩趋势以外的可行解空间的探索，导致算法对全局的寻优能力较差。因此，需要改进算法在空间中的收缩趋势，在原有长度收缩的基础上增加对解空间的探索能力，从而增强算法的全局寻优能力。算法的收缩趋势由弹性绳节点的更新算法确定，因此需要针对弹性绳节点的更新算法进行改进。

为了提高节点更新算法对可行解空间的搜索能力，引入由m维节点组成的弹性绳路径组，每一维节点均可表示一条弹性绳路径，并且均在算法开始时随机初始化。路径节点的编码方式如式（4）所示：

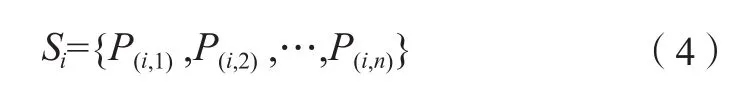
式中，P(i,j)表示第i维弹性绳的第j个节点，i≥ 2,n≥ 3。

因此，改进后的弹性绳节点收缩公式如式（5）所示：

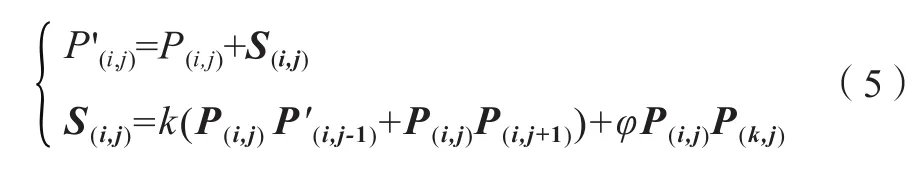
式中，S(i,j)表示节点P(i,j)的运动位移(i=2,3,…,n-1)并且k∈(0,1)；φP(i,j)P(k,j)表示基于不同维度下的节点对可行解空间的搜索位移，φ∈(0,1)为随机数。

由更新后的节点搜索算法可知，在弹性绳算法运算初期，由于不同维度间同一节点的位置差异和附加随机数，算法会在搜索位移的作用下在可行解空间扩大搜索范围，并对节点的位置进行更新，增大算法对可行解空间最优解的搜索能力。在算法运行后期，由于不同维度的弹性绳路径在收缩作用下均趋于全局空间的最优路径，不同维度间的节点位置趋于一致。由式（5）可知，这时节点更新公式的搜索位移项将趋于零，路径节点最终收敛于全局最优路径。

4 仿真分析

在无人机路径规划阶段需要的已知信息包括环境中的障碍和威胁、路径的起点和无人机的目标点等要素。无人机在执行任务过程中的动态避障行为不在本文的考虑范围内。

本文主要考虑在真实环境中进行无人机路径规划的任务，这意味着需要考虑到真实环境中的地形信息，因此，在无人机任务规划阶段利用数字高程模型来描述无人机任务规划区域的空间信息。数字地图高程模型是通过数字列阵来地面高程的仿真模型，该数字阵列按一定的空间划分规则排序。本文将环境中的障碍设置为一系列不同大小的半球，并且将这些障碍与地形信息进行结合，制作了无人机路径规划环境的场景地图。融合后的无人机任务规划环境地图如图3所示。

图4为弹性绳算法改进前在无人机路径规划过程中算法陷入局部最优解的情况。从图4中可以看出，无人机路径的节点在场景中的一个障碍处向着错误的地方运动，并且在该障碍物处陷入了局部最优解。

利用设计的弹性绳算法对场景中的单架无人机进行路径规划，所得结果的如图5和图6所示。

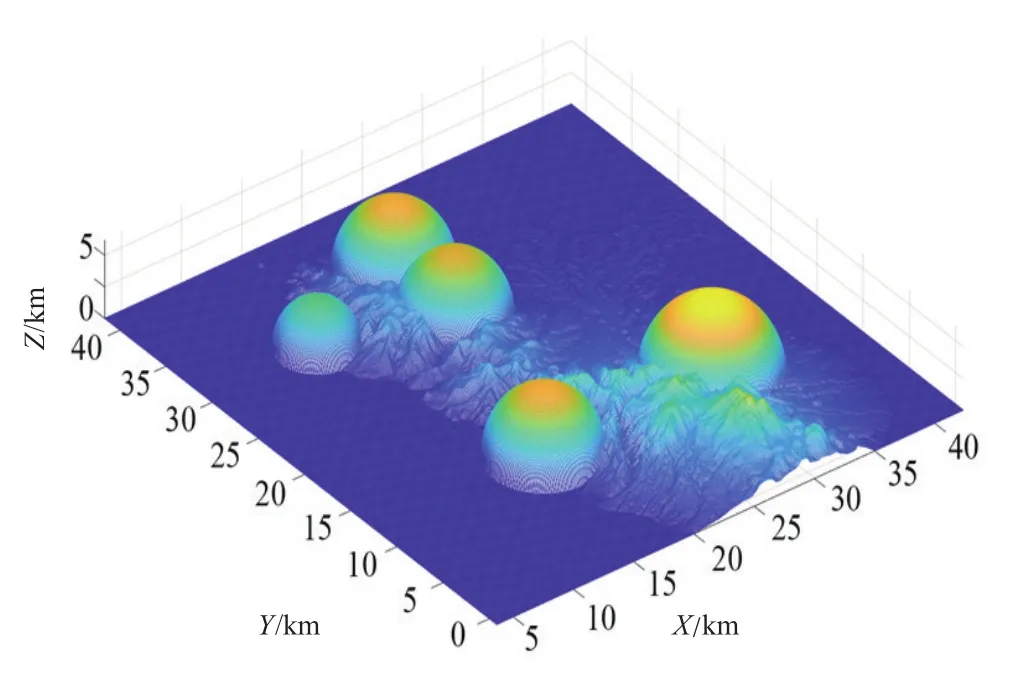
图3 无人机任务规划环境地图

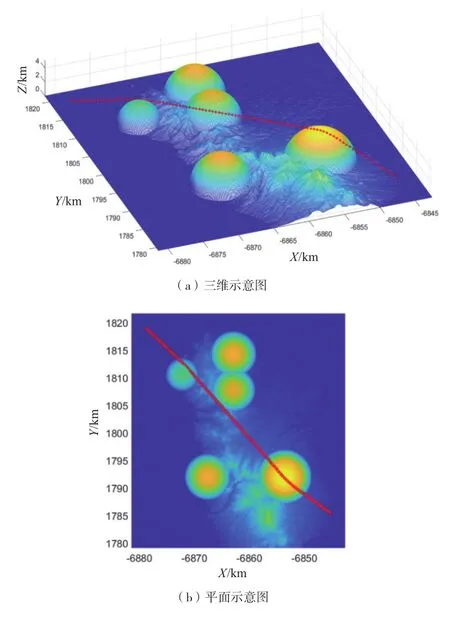
图4 陷入局部最优的情况示意

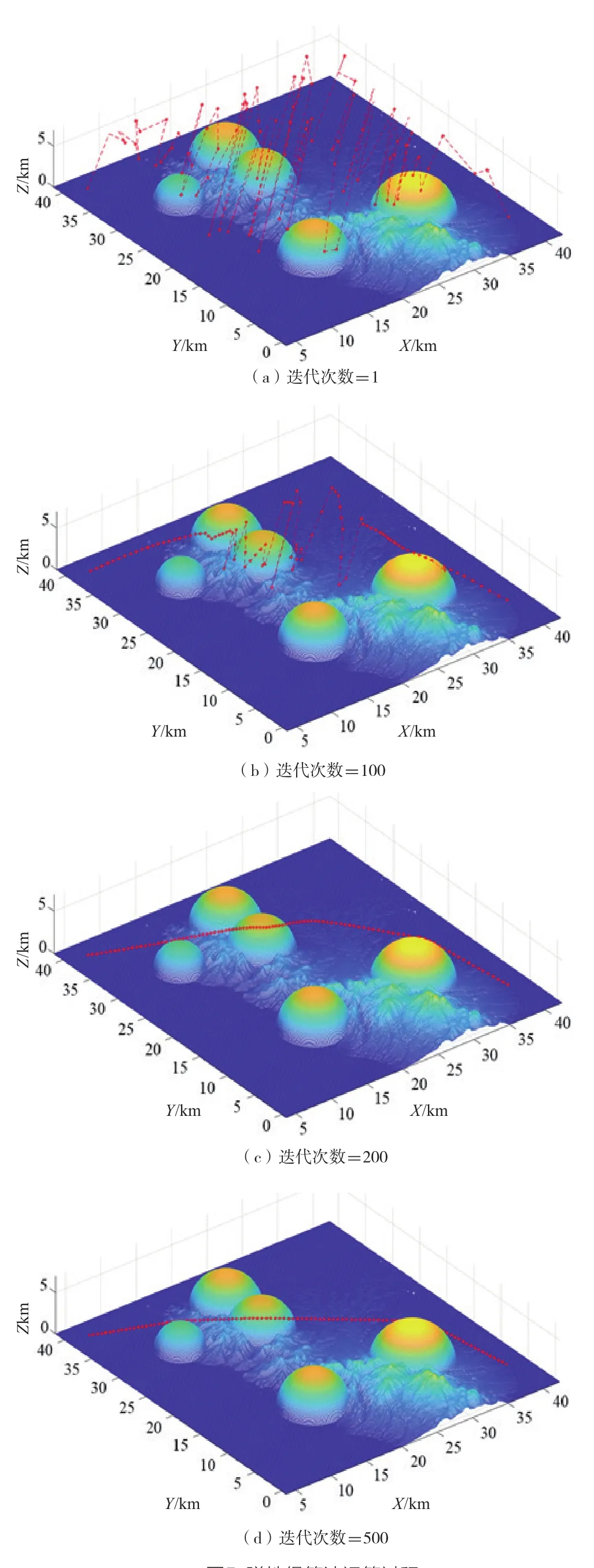
图5 弹性绳算法运算过程

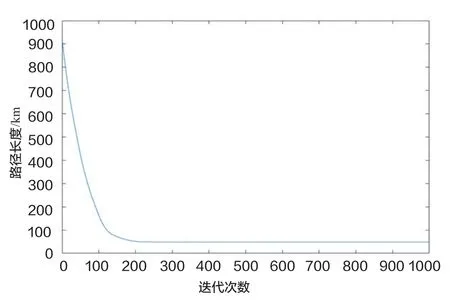
图6 路径长度随迭代次数的变化

弹性绳算法是一种基于几何关系对组成路径的所有节点进行收缩迭代的路径规划算法，通过对组成弹性绳的各个节点位置进行逐次更新迭代，使初始路径的长度向着长度减少的方向逐渐收缩，并且最终收缩到空间中的最优位置。

无人机在真实地形和存在障碍物的场景中的路径规划过程如图5所示。在仿真初始阶段，算法首先在任务空间中随机初始化出一组弹性绳节点，如图5（a）所示。随着弹性绳算法的迭代，在运算过程中的路径变化如图5 （b）和图5（c）所示。最终经过运算得到的最短路径结果如图5（d）所示。

任务空间中弹性绳的长度代表无人机任务路径的长度，由相邻路径段长度之和表示。在弹性绳算法运算过程中，无人机路径的长度随迭代次数的变化如图6所示。从图中可以看出，随着弹性绳算法的不断迭代，无人机路径的长度不断减少，并且最终达到空间最短距离。从实验结果可以看出，弹性绳算法可以用在无人机路径规划方面。

5 结束语

弹性绳算法是一种基于几何关系对组成路径的所有节点进行收缩迭代的路径规划算法，通过对组成弹性绳的各个节点位置进行逐次更新迭代，使初始路径的长度向着长度减少的方向逐渐收缩，并且最终收缩到空间中的最优位置。弹性绳算法在运算初始时随机初始化了一条连接规划起点到终点的原始路径，保证了该路径是存在的，将路径规划问题转换为路径的优化问题。另外，该算法的节点更新规则简单，收敛速度快，可以直接应用到复杂的场景当中。