动力电池SOC估计的一种新型鲁棒UKF算法*
谈发明,赵俊杰,王 琪
(1.江苏理工学院信息中心,常州 213001; 2.江苏理工学院电气信息工程学院,常州 213001)
前言
动力电池荷电状态(state of charge,SOC)无法直接测量,但可以采用滤波算法根据电池的其它可观测数据来间接估计,如果电压观测数据出现较大偏差或受到外界环境干扰,会使数据中包含野值,野值的出现将导致滤波算法的精度和稳定性下降,收敛慢,甚至引起发散。因此,滤波算法的鲁棒性能研究对动力电池管理系统十分重要。
无迹卡尔曼滤波(unscented Kalman filter,UKF)算法利用无迹变换在估计点附近确定采样点,通过这些样本点逼近状态向量后验概率密度函数的均值和协方差,可避免由于线性化而导致的跟踪误差,算法容易实现,精度高[1-2]。但其抗野值方面的鲁棒性仍有较大优化提升空间。针对这一问题,文献[3]和文献[4]中使用极大似然准则和Sage-Huga的改进UKF得到系统次优递推噪声估计器代替UKF算法中的平滑估计值的方法抑制滤波发散,解决观测噪声统计特性未知的问题。但其状态噪声方差在SOC估计过程中自适应调整容易导致估计波形抖振。文献[5]中提出UKF算法结合窗口和随机加权的方法,通过调整每个窗口的随机权重细化所获得的窗口估计,但该方法的SOC估计稳定性较差。文献[6]中使用UKF滤波的残差χ2检验,根据其统计特性判断野值噪声,并采用平滑窗口实现对野值噪声的有效隔离,但其在变工况和建立的电池模型存在差异条件下检验阈值比较难以确定。文献[7]和文献[8]中提出在UKF算法中引入M稳健估计的IGGⅢ法计算权因子,以此因子实时调整观测噪声协方差以及增益矩阵,该方法在一定程度上可以有效克服野值影响,但在SOC初值设定误差较大的情况下收敛速度稍慢,且对斑点型野值的抗干扰效果不尽理想。
在上述研究的基础上,本文中提出的改进鲁棒UKF算法核心在于将SOC估计过程分为单纯抗野值和强跟踪两个阶段,单纯抗野值阶段将观测噪声模型定义为归一化受污染正态分布模型(scaledcontaminated normal distribution model,SCNM),利用贝叶斯定理计算野值出现的后验概率,以此作为加权系数自适应修正滤波增益和状态协方差,该方法对野值具有很好的抗干扰效果。但在SOC初值设定存在误差情况下,单纯抗野值模式会误将正常电压观测数据当作野值,滤波器仅以小增益控制量对跟踪目标跟踪,会导致估计过程收敛速度慢甚至引起发散。因此,在算法的起始阶段引入次优渐消因子的强跟踪方式对目标进行快速跟踪,设定观测残差阈值实时检测跟踪情况,跟踪到目标后再自动切换到单纯抗野值模式,弥补了单纯抗野值的缺陷。改进鲁棒UKF算法对野值干扰具有很强的矫正作用,SOC估计过程收敛速度快,鲁棒性能好,估计精度高。
1 动力电池建模
为使建立的模型能很好体现电池非线性特性,获得较高拟合精度,采用由Shepherd,Unnewehr U-niversal和Nernst 3种常用电池模型合并而成的复合模型作为动力电池模型[9],结合安时计量法,定义电池模型方程如下。
状态方程:

式中:状态量xk为k时刻SOC;ik为k时刻电池的电流值,作为电池模型的控制量;η为充电效率;C为电池的额定总容量;Δt为采样周期;状态噪声wk为满足正态分布的高斯白噪声,即 wk~N(0,Qk),Qk为状态噪声方差阵。
观测方程:

式中:观测量yk为k时刻电池的端电压;Eo为电池开路电压;RΩ为电池欧姆内阻;k1,k2,k3,k4为拟合系数;暂假定观测噪声vk为满足正态分布的高斯白噪声,即 vk~N(0,Rk),Rk为观测噪声方差阵。
2 UKF估计电池SOC方法
针对式(1)和式(2)建立的电池模型,利用UKF算法估计SOC的主要递推步骤如下。
(1)状态和协方差初始化

(2)采用SVD法分解Pk-1,并计算产生2n+1个Sigma点:
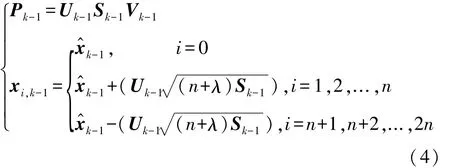
式中:对角矩阵 Sk-1由 Pk-1的奇异值构成;Uk-1和Vk-1为酉矩阵;xi,k-1对应前-时刻状态估计结果x^k-1所产生的第i个Sigma点。
(3)确定Sigma点对应的权系数:

式中:权系数ω上标m表示均值权,c表示协方差权;β为状态分布参数;α(0≤α≤1)为点集到均值点的距离;λ=α2(n+ε)-n为尺度调节因子,其中,ε为次级尺度调节因子。
(4)将Sigma点集代入电池模型方程,通过加权求和计算状态和相关协方差的时间更新结果:

(5)估计结果更新:

式中:Kk为滤波增益;ζk为系统观测残差。
3 基于UKF的抗野值改进分析
3.1 应用SCNM噪声模型
若在电池的电压观测数据中存在野值情况下,仍先验假设观测噪声为正态随机分布显然不合适[10]。但对于整个数据序列而言,野值的出现概率较低。因此,本文中观测噪声模型借鉴了SCNM噪声模型,该模型用两个归一化的加权正态分布来逐次逼近可能具有野值的观测噪声的误差分布,将野值视为一个相对于正态分布拖尾更大的误差分布[11]。因此,将式(2)观测方程中的观测噪声 vk分布重新定义为
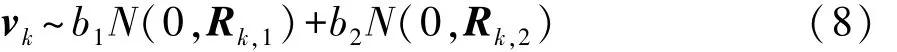
式中:b1和 b2为权系数,其中,b2∈(0,0.15),b1=1-b2;Rk,1为正常值观测噪声方差,Rk,1=σ2v,其中,σ2v为假定己知的电压观测方差;Rk,2为野值观测噪声方差,Rk,2=d2Rk,1,d>1。
在任何测量环境下,Rk,2比 Rk,1具有更大的不确定性,因此,野值观测噪声需要用较小的权系数b2来修正。在未出现野值干扰时,正常值观测噪声对滤波效果有主导作用,确保算法对目标的跟踪能力。
3.2 基于Bayes定理的改进
观测噪声模型定义在SCNM模型的基础上,利用Bayes定理分别计算电压观测数据中正常值和野值出现时的后验概率,并以此作为加权系数来调整滤波增益和状态协方差,能有效克服野值产生的不利影响,改进方法简单易行,物理意义明确。
首先,根据电池模型观测方程定义正常值和野值对应的新息协方差:

式中:Dk,1为 k时刻正常值新息协方差;Dk,2为 k时刻野值新息协方差。
利用Bayes定理,计算后验加权概率:

式中:ak,1为 k时刻的正常值后验加权概率;ak,2为 k时刻的野值后验加权概率。
利用 ak,1和 ak,2作为加权系数将式(7)的滤波增益Kk修正为加权和的形式:

进一步利用 ak,1和 ak,2作为加权系数来修正状态协方差:

其中状态协方差控制矩阵Mk和Nk定义如下:
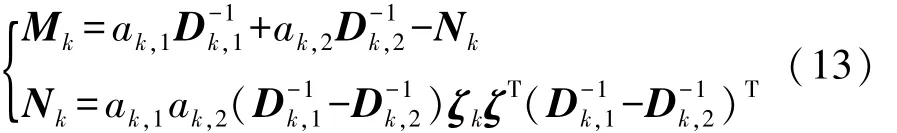
3.3 引入次优渐消因子
由于电池使用过程不可避免存在自放电或馈电现象,使电池当前的SOC实际值与管理系统停止工作前记录保存的SOC值不相同,电池再次启动时就会存在SOC初值设定误差的问题。若直接用前述单纯抗野值改进的UKF算法进行估计,在算法起始阶段会将电压观测正常值误认为野值,从而导致算法收敛慢甚至引起发散。因此,在算法初始阶段引入了基于强跟踪滤波原理的次优渐消因子[12],在线调节滤波增益,迫使观测残差相互正交,使算法具有自适应跟踪状态变化的能力。
观测残差方差阵Vk定义为
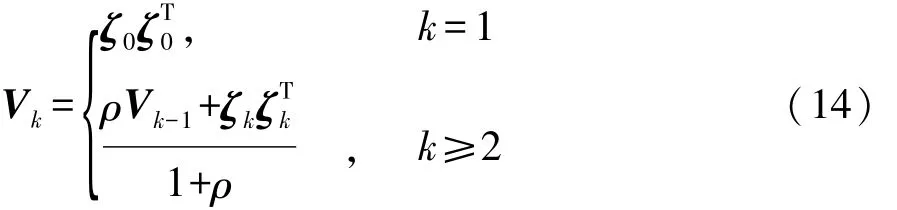
式中ρ为遗忘因子,0.95≤ρ≤0.98。
改进型次优渐消因子λk定义为

由于SOC值在估计过程中变化范围小,利用引入次优渐消因子的UKF算法估计电池SOC时,会存在估计波形波动性大的问题。鉴于此,设计了软化因子μ作为权系数修正λk,μ的取值对估计效果影响较大,通常取值远小于1。
利用λk修正状态预测协方差:

引入次优渐消因子的强跟踪方式具有很强的抗干扰性能,无论SOC估计值是否达到稳定状态,都具有较强的实时跟踪能力[12]。需要注意的是,UKF算法应用于强跟踪方式时,观测噪声vk须使用满足正态分布的高斯白噪声模型,而不能使用式(8)定义的SCNM噪声模型。
3.4 改进算法实现步骤
改进鲁棒UKF算法针对动力电池SOC估计的简要过程:在估计初始阶段采用引入次优渐消因子的强跟踪方式对目标进行快速跟踪,实时检测系统残差ζk的绝对值是否小于设定的阈值ε,即当|ζk|<ε时,说明算法已经收敛并跟踪到目标,强跟踪方式停止工作,后继的估计过程全部采用单纯抗野值模式。具体实现流程如图1所示。

图1 改进型鲁棒UKF算法实现流程
4 数据采集与模型参数辩识
4.1 样本数据采集
实验采用汽车高级仿真软件ADVISOR获取通用电动汽车行驶过程中的电池参数,研究对象为聚合物动力锂电池,电动汽车整车关键参数见表1。

表1 整车关键参数
电池和外部环境的初始温度设定为20℃,测试工况采用美国城市道路典型工况(urban dynamome-ter driving schedule,UDDS),全长 11.99 km,运行时间 1 370 s,最 大 车 速 56.7 km/h,平 均 车 速19.58 km/h,路况复杂度较高。实验以1 Hz的频率采集电池工作过程中的电压、电流及SOC,总共可获取1 370组,4 110个样本数据。
图2为电池工作过程中采集到的样本数据。由图可见:大多数情况下电池处于小电流充、放电状态;实测的电池SOC参考值的整体变化趋势缓慢下降。

图2 电池样本数据
4.2 电池模型参数辩识
利用与式(2)对应的电池模型观测方程各参数,要求输入量为持续激励信号[9],UDDS工况下的电池样本数据能够满足此要求,具体辩识步骤如下。
(1)定义数据向量 Hk=[1 ikxk1/xkln(xk)ln(1-xk)];待估向量=[E0R k1k2k3k4];最小二乘形式为,其中 ek为误差函数。
(3)利用式(17)递推公式迭代求解,直至达到最大迭代次数。

式中:Lk为增益矩阵;Gk为协方差矩阵。
图 3为参数 E0,R,k1,k2,k3和 k4利用递推最小二乘法辨识的收敛情况。

图3 参数收敛变化
从图3可看出,各参数辨识曲线有相似的收敛特性,均在迭代约1 100次后趋于稳定,收敛后稳定性好。表2为辨识得到的各参数值。

表2 模型参数辩识结果
采用相对误差RE和平均相对误差MRE两个指标评价模型估计精度,定义如下:

式中:yj为样本观测值;y^j为样本估计值;l为样本数。
UDDS工况条件下,端电压实测与仿真结果如图4所示。可以看出两者之间的吻合度较高。其中,RE最大值为0.39%,MRE为0.1%,该数据充分说明在UDDS工况下,电池模型的观测方程参数辨识结果具有较高的精度,辨识方法可行有效。
5 仿真结果分析
为验证采用改进鲁棒UKF算法进行动力电池SOC估计的精度、跟踪能力、鲁棒性和泛化能力,从抗野值鲁棒性、状态初值误差收敛性,变工况泛化性几个角度进行仿真分析。

图4 UDDS工况端电压实测与仿真值对比
改进鲁棒UKF算法关键参数的设置:b1=0.1,b2=0.1,Rk,2=25Rk,1,ρ=0.98,μ=10-5,ε=0.2。
5.1 抗野值鲁棒性分析
采用由成片出现的斑点型噪声作为野值干扰,检验改进算法的鲁棒性能。在图2电压数据的第230至279 s范围内加入斑点型噪声作为野值,形成如图5所示受干扰的电压观测序列。

图5 斑点型野值干扰电压序列
图6 为SOC估计过程中,后验加权概率a1和a2参数的变化情况。在受到斑点型野值干扰时间段,基于Bayes定理求解得到的正常值后验加权概率a1为0,野值后验加权概率a2为1,这种现象说明这个时间段的电压观测值存在异常,受到了野值污染。
当系统判断出当前电压观测信号为野值时,利用当前时刻的后验加权概率a1和a2作为加权系数自适应地修正滤波增益和状态协方差。

图6 后验加权概率参数变化情况
滤波增益K的变化情况如图7所示,在受野值干扰时段,其数值上为接近0的极小值,主要因为:
(1)式(11)右边第1项受正常值后验加权概率a1和正常值新息协方差控制,该项在受野值干扰阶段被a1修正为0;
(2)由于SCNM噪声模型定义的野值观测噪声方差较大,约为正常值的25倍,导致野值新息协方差始终相对较大,尽管野值后验加权概率a2为1,式(11)左边受野值控制的第2项仍能保持很小的值。

图7 Kalman增益变化情况
鉴于以上两点,在野值出现阶段,滤波增益始终保持相当小的控制量,可以抵消观测残差骤大对SOC当前估计值精度的影响。
状态协方差P的变化情况如图8所示,在受野值干扰时段内P延续了干扰前的变化趋势,因为后验加权概率a1将式(13)当前时刻的状态协方差控制矩阵N修正为0,导致当前时刻状态协方差控制矩阵M仅受野值后验加权概率a2和野值新息协方差影响,根据滤波增益部分的自适应控制方法可知,在野值出现时,M会一直保持相当小的值,以使当前时刻的状态协方差与前一时刻相差不大,保持原有变化趋势小幅调整,这样可保证下一时刻的SOC状态预测值不会因状态协方差的缘故而出现太大偏差。

图8 状态协方差变化情况
改进鲁棒UKF算法的估计效果如图9所示,几乎看不出野值干扰的影响,取得良好的抗野值效果。而且,在非野值干扰区域,估计结果具有高精度,估计波形平滑。这是因为在该区域,正常值后验加权概率a1和正常值观测噪声方差对估计结果起主导作用,由图6中a1的变化情况可以看出,作为权值的a1绝大部分情况下处于大概率值状态,SCNM噪声模型中定义的正常值观测噪声方差较小,两者结合可以有效调节滤波增益和状态协方差,保证算法的跟踪速度和精度。

图9 存在斑点型野值估计结果
5.2 SOC初值误差收敛性分析
为检验改进鲁棒UKF算法估计SOC时对其初值设定的依赖程度、响应时间和收敛性能,在状态初值分别为0.5和0.9的设定条件下,图10描述了改进型鲁棒UKF算法引入次优渐消因子前后的收敛情况。
UKF算法在单纯抗野值模式工作时,会将状态初值存在误差的起始电压观测正常值误认为野值,由上述分析可知,滤波器以极小的增益控制量对目标进行跟踪,导致收敛跟踪速度很慢;而算法引入了次优渐消因子后能很快跟踪到目标,所有曲线在第7 s左右收敛至参考值附近,跟踪响应时间短,收敛速度快。主要由于状态初值设定误差通过系统残差体现,在引入了基于强跟踪原理的次优渐消因子后,其敏感性对增益矩阵有强化作用,能够快速跟踪到目标。因此,在状态初值存在误差的情况下,改进鲁棒UKF算法的收敛性能优异。
5.3 变工况泛化性分析
选用西弗吉尼亚州际行车工况(west Virginia interstate driving schedule,WVIDS)对改进鲁棒UKF算法进行变工况测试。因为WVIDS工况正常电压样本值在1 150~1 250 s范围内的热态过渡阶段有相对较大波动,可以检验算法变工况复杂条件下的跟踪能力。在此基础上,在正常电压样本值的第230至279 s加入斑点型噪声;在第 200,400,600,800和1 000 s处加入离散形式的孤立型噪声。两者组成复合噪声作为野值对电压样本正常值干扰,进一步检验算法变工况复杂条件下的抗野值鲁棒性能。受野值干扰后的电压观测序列如图11所示。
利用改进鲁棒UKF算法分别与强跟踪无迹卡尔曼滤波算法(strong tracking-unscented Kalman filter,ST-UKF)以及UKF算法进行估计效果比较,在相同参数设置条件下检验各自综合性能。其中,SOC初值设定为0.5。

图11 复合噪声野值干扰电压序列
图12 为WVIDS工况下不同算法估计结果比较。从图中可以看出,UKF算法在状态初值存在误差情况下收敛慢,当成片连续斑点型野值出现时,由于较长时间无法获取电压观测正常值信息,相关观测新息方差无法实时更新,导致后续估计结果发散。但UKF算法自身有一定的鲁棒性,能够对孤立型野值产生抗干扰作用;ST-UKF算法的SOC估计精度不但在野值出现时受到严重影响,由图12(a)中的局部放大图可以看出,观测电压正常值的短时较大幅度波动都会引起SOC估计值较大范围偏离参考值,这是由于系统观测残差突然增大,而强跟踪的敏感性会导致滤波增益也随之剧增,使SOC估计结果产生较大误差。

图12 WVIDS工况下不同算法估计结果比较
图12 表明,改进鲁棒UKF算法在WVIDS工况中应用的性能最优。但不难发现,该算法在小噪声平坦区域精度要略低于ST-UKF算法,主要由于SCNM噪声模型的定义中包含了小系数加权野值观测噪声,尽管这一噪声采用了小权系数以及保持较大的野值新息协方差,但还是会对滤波增益的控制能力产生一定影响,从而造成跟踪速度和估计结果精度略微降低。这也说明在这一段估计区域精度与稳定性相互矛盾。尽管如此,以较小的精度差来换取算法的鲁棒性和估计波形的平滑性还是可取的。
为能更清晰说明改进鲁棒UKF算法的精度优势,选取估计时间100 s以后,3种算法均收敛到参数值附近的估计结果进行统计。根据式(18)定义的误差标准,3种算法的估计误差见表3。

表3 平均相对误差结果对比
从表3可以看出,改进鲁棒UKF算法精度最优。在电池SOC初值误差较大、掺杂多种类型野值和变工况条件下,改进鲁棒UKF算法跟踪精度和速度优势明显,且估计波形平滑,波动抖振小,能够充分说明算法改进的有效性和泛化性。
6 结论
(1)利用SCNM噪声模型和Bayes定理改进了UKF算法估计动力电池SOC过程中的抗野值鲁棒性能,但单纯抗野值改进会存在将估计起始阶段的电压观测正常值误认为野值的缺陷,因此,算法在初始阶段引入了次优渐消因子对目标强跟踪,弥补上述缺陷。
(2)对改进型鲁棒UKF算法从抗野值鲁棒性、SOC初值误差收敛性和变工况泛化性几个角度验证了算法改进的有效性。
(3)不足之处在于改进算法在估计波形平坦区域的精度要略低于ST-UKF算法,但以较小的精度误差替换算法稳定性是值得的。

