桩土作用计算方法在系缆墩桩基设计中的应用

竺奇乐

(1.中船第九设计研究院工程有限公司， 上海200063；2.上海海洋工程和船厂水工特种工程技术研究中心， 上海200063)

0 引 言

停靠VLCC的系缆墩是重要的码头设施，其承受水平荷载的能力直接影响大型船舶的系缆安全[1]。系缆墩结构型式一般为高桩墩台，由上部的墩台和下部的桩基构成。在承受较大的单边或双边水平系缆力时，墩台及桩基将产生明显的位移和转动，因此桩基的内力分析和变形计算对于结构工程设计而言尤为重要。然而，选择不同的桩土作用计算假定方法得到的结果往往有差异，给桩基设计带来困难。本文基于海外工程实例，对系缆墩结构中桩基常用的两种桩土作用计算方法，即假想嵌固点法和m法分别进行空间有限元分析，并对比国内外规范或手册，确定假想嵌固点深度的计算方法，为类似结构在砂土地基中的设计提供了一定的借鉴。

1 桩土作用计算方法

1.1 假想嵌固点法

假想嵌固点法认为：桩身入土达到一定深度后受土体约束而嵌固，嵌固点处的桩身节点只考虑轴向自由度，国内港工规范[2]及国外桩基计算手册[3]均建议采用该方法作为模拟桩承受水平力时桩土的相互作用，但确定嵌固点深度的计算方法有所不同。国内外的计算方法对比如表1所示。

表1 国内外嵌固点深度计算方法对比

图1 适用于砂土的太沙基曲线[3]

1.2 m法

m法即工程实践中最为常用的竖向线弹性地基法[4]，一般适用于桩在泥面处的水平位移小于10 mm的情况。该方法应用广泛，基本原理是：假设土的水平地基抗力系数随深度呈线性增加。其计算公式为

K=mZ

(5)

式中：K为土的水平地基抗力系数，kN/m3；m为土的水平地基抗力系数随深度增大的比例系数，kN/m4，宜通过单桩水平静载试验确定，当无试桩资料时，可按相关经验取值；Z为计算点的深度，m。

2 海外工程实例

中东地区某大型造船与海工基地的1#突堤码头海侧端通过栈桥与1#系缆墩相连，设计靠泊船型为载重量3×105t的VLCC。

2.1 结构概况

上部墩台结构长15.00 m、宽15.00 m、厚2.50 m，由14根直径为1 016 mm、壁厚为22 mm的钢管斜桩支承；墩台顶标高为+4.50 m CD (“Chart Datum”的缩写，意为“标高是基于海图基准面”)，设计泥面为-11.00 m CD，如图2所示。该系缆墩设计为双边靠船，顶面设置1个200 t双系船柱。

图2 配置200 t双系船柱墩台1#系缆墩剖面图

2.2 设计荷载

(1) 结构自重：钢筋混凝土结构重度为25.0 kN/m3，钢管桩重度为78.5 kN/m3。

(2) 均载：q=5 kPa。

(3) 船舶系缆力：2 000 kN/个，按照垂直系缆角为15°、水平系缆角为30°进行计算。

(4) 波浪力：所在港池水域外侧有防波堤掩护，不考虑波浪力的影响。

2.3 设计水位

工程所在区域设计水位如表2所示。

2.4 地质条件

根据地质报告，工程所在区域的地层主要为粉砂及砂岩，主要岩土分层及参数如表3所示。

表2 工程区域的设计水位

表3 地基土层参数

2.5 有限元计算模型

Autodesk Robot Structural Analysis是一款集合了结构建模、结构计算和结构设计的可视化空间有限元计算软件。该软件允许用户创建结构模型，开展计算并获取结果，其强大的后处理功能对设计的结构可直接生成相关计算文件。本高桩墩台结构的桩基内力分析选用该软件。

本例中高桩墩台三维有限元模型如图3所示，其中：墩台采用SHELL单元，钢管桩采用BAR单元，桩土相互作用分别采用假想嵌固点法和m法进行模拟，并开展比较研究。在基于假想嵌固点法的模型中，桩基在泥面以下的长度为计算的嵌固点深度(根据国内外规范的计算结果对比如表4所示，为满足海外工程要求，本模型选用国外桩基手册的计算结果)，桩端约束为固结；基于m法模型的桩长即为实际桩长，桩基入土部分视为竖向弹性地基梁[5]，以深度每隔1 m的水平向“土弹簧”(地基土m值根据所在岩土层选取，如表3所示)模拟桩土效应，桩尖除了水平向的弹簧约束外，还附加z向的平动约束。

图3 1#系缆墩三维有限元模型

表4 国内外规范或手册确定的水平力作用下桩基嵌固点深度计算对比

2.6 计算组合及工况

本例在计算桩基内力及变形时，遵循工程所在国家的规范，分别计算强度设计极限状态(用于验算结构的强度)和允许应力设计极限状态(用于验算结构的裂缝和变形等)两种极限状态下桩基的弯矩、轴力(包括压桩力和拉桩力)及结构变形，严格按照规范选取各设计荷载的分项系数。本例中的计算工况如表5所示。

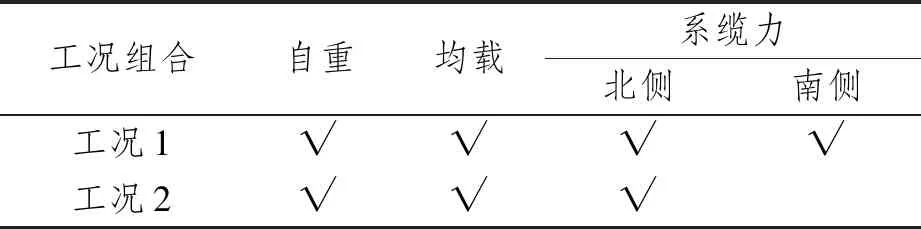
表5 系缆墩桩基计算工况

2.7 计算结果

基于假想嵌固点法和m法两种桩土作用计算方法，利用Autodesk Robot空间有限元软件软件进行分析，两种极限状态、两种工况下墩台桩基的弯矩、轴力(包括压桩力和拉桩力)以及桩顶位移的计算结果如表6、表7和图4所示。

表6 强度设计极限状态下桩基计算结果(工况1)

表7 强度设计极限状态下桩基计算结果(工况2)

图4 系缆墩桩基桩顶位移计算结果(允许应力设计极限状态)

计算结果表明：

(1) 轴力：两种计算方法的最大压桩力和最大拉桩力所在的桩位完全相同，但假想嵌固点法计算的桩力明显大于m法计算的桩力(平均差异61%)，这表明在桩身没有水平向“土弹簧”约束的条件下，墩台桩力的分布较为不均，极值较为凸显。

(2) 弯矩：两种计算方法的最大弯矩所在桩位基本相同，但m法计算的弯矩大于假想嵌固点法计算的弯矩(平均差异31%)，这是因为假想嵌固点法确定的计算桩长小于实际桩长，受弯长度小，因此计算的弯矩就偏小。

(3) 变形：在两种计算方法中，m法计算的桩顶位移明显大于假想嵌固点法计算的桩顶位移(平均差异69%)，桩顶位移计算值存在差异的主要原因与弯矩的计算结果类似，m法的计算桩长为实际桩长，明显大于假想嵌固点法确定的计算桩长，在相同水平力的作用下，前者的位移更大。

3 结 论

针对承受较大水平力的系缆墩桩基设计，结合中东地区某大型造船与海工基地的工程实例，通过空间有限元软件，对比分析了两种桩土作用计算方法在桩基设计中的应用，为类似墩台结构的桩基设计提供一定参考，主要结论如下：

(1) 系缆墩结构的桩基在承受较大水平作用力时，桩基的入土深度宜满足弹性长桩条件。桩基内力和变形的确定可选用假想嵌固点法和m法模拟桩土的相互作用。

(2) 假想嵌固点法假定受水平作用力的桩基处于悬臂状态，确定嵌固点深度的经验方法在国内外规范及手册中有所差异。本文通过对比研究得出结论：在砂土中打入桩，国内外不同方法确定的嵌固点深度相近，基本在5～6倍桩径范围内。

(3)m法假定泥面以下的地基土对桩基起水平约束作用，该计算方法能更为真实地反映桩基所处的地质条件，与假想嵌固点法相比，m法的有限元建模过程相对复杂，须模拟桩基入土后各地基土层的“土弹簧”。通过空间有限元对于系缆墩结构的桩基内力及变形的对比分析得出：在砂土中打入桩时，采用以m法计算弹性长桩的轴力以及以假想嵌固点法确定弹性长桩的弯矩和变形作为设计依据是偏危险的。在实际工程设计中，应对不同桩土作用方法的计算结果作综合考虑。