灰色神经网络组合模型在沉陷监测间断插补中的应用*

刘维康

（河南理工大学测绘与国土信息工程学院 焦作 454000）

1 引言

矿区开采沉陷监测往往是在开采工作面区域布设一定的观测线，利用各种仪器与手段对监测点进行持续观测，获得地表的沉陷数据。但在实际的观测过程中，通常会由于气候条件、环境因素、人为原因等造成观测数据的间断。而地表沉陷测数据的间断可分为以下几种情况：1）在雨季时地表观测点被积水淹没；2）由恶劣天气、仪器故障等因素导致观测无法进行；3）某期实测资料误差较大导致监测数据失真。为了研究矿区地表沉陷的规律，保证有限次观测数据的完整性，对缺失数据进行插补估值，具有重要的意义。

灰色系统理论［1］以“部分信息已知，部分信息未知”的不确定性系统为研究对象，能较好地预测变化的趋势，而且要求样本数据少、短期预测精度高。而Elman神经网络［2］具有动态特性好、非线性关系处理能力强等特点，对于非精确性规律具有较强的自适应、自主学习能力。将灰色系统理论与Elman神经网络通过熵权法［3］组合起来，可充分发挥各自的优势，进一步提高预测精度。因此，本文对已有的相邻测点的可靠实测资料进行灰色关联度分析，采用关联性强的监测点数据建立灰色GM（0，n）模型与Elman神经网络模型，并将其进行组合，以期得到精度较高的沉陷监测间断插补值。

2 矿区沉陷数据预测模型

2.1 灰色关联分析模型

灰色关联分析［4～5］是依据数据曲线几何形状的相似程度来判断相关因素序列与系统特征序列的关联性，若数据序列间的变化趋势越相同，则认为数据序列间关联度越高。其建模步骤如下。

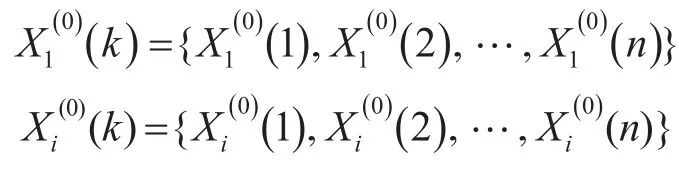
则将原始数据进行初值化处理：

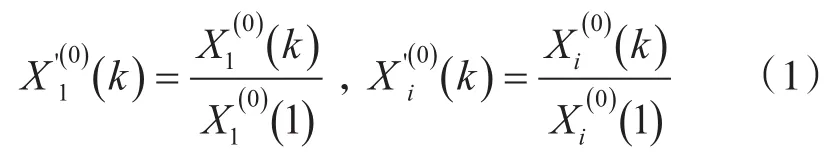
2）计算关联系数

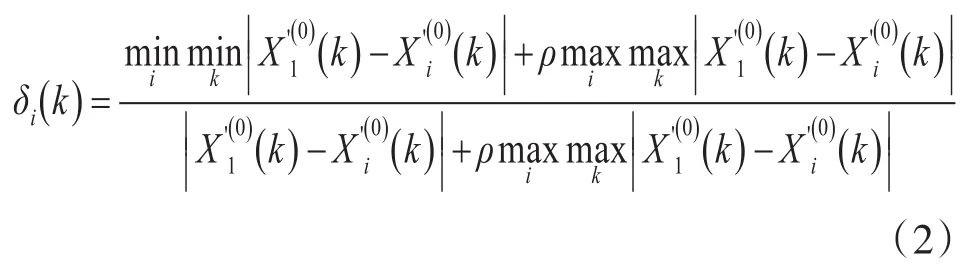
3）计算关联度

2.2 灰色GM（0，n）模型［6～8］

其一次累加生成序列为

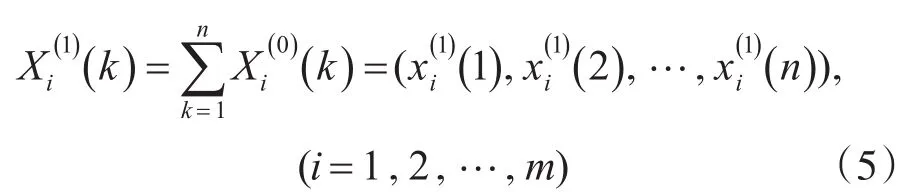
则灰色GM（0，n）模型为

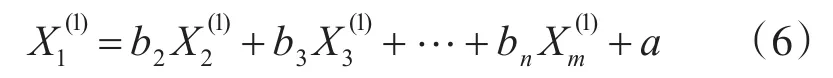
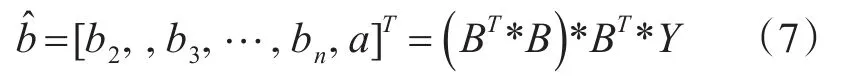
其中：

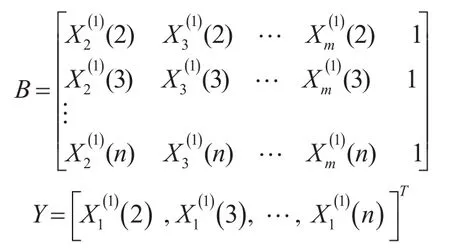
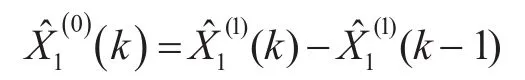
2.3 Elm an神经网络

Elman神经网络［9］是一种局部回归多层神经网络，它包含输入层、隐含层、承接层和输出层。其输入层、隐含层和输出层的连接类似于前馈网络，输入层的单元仅起信号传输作用，输出层起信号加权作用。隐含层单元的传递函数可采用线性或非线性函数，承接层又称为上下文层或状态层，它用来记忆隐含层单元前一时刻的输出值，可以认为是一个一步延时算子［10］。在Elman神经网络模型中，设输出层和连接层的传递函数为线性函数，隐含层的传递函数为非线性函数，其状态空间表达式［11］为

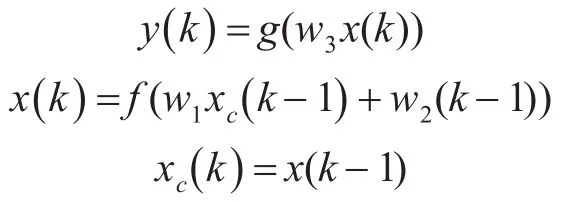
Elman神经网络能够以任意精度逼近非线性映射，通过灰色关联分析确定影响因子，作为模型的输入建立Elman神经网络模型［12］。其实现步骤：

1）通过灰色关联分析确定与输出数据关联性强的输入数据，将其归一化到［-1，1］；

2）设置网络参数。Elman神经网络预测精度设为1e-5，最大训练次数为50000次，学习率为0.05，传递函数取S函数，并采用traingdx函数作为训练函数；

3）将训练好的Elman网络模型，采用SIM函数进行仿真预测。

3 基于熵权法的组合模型

3.1 基于熵权法确定权重

根据信息熵的性质，组合预测模型中某单项模型误差的信息熵越小，变异程度越大，不确定度越大，则该单项模型的权重系数就越小；反之，若某项模型的指标值变异程度越小，则模型的权重就越大［13～15］。因此，利用信息熵原理计算各单项的模型在组合预测中的权重系数。

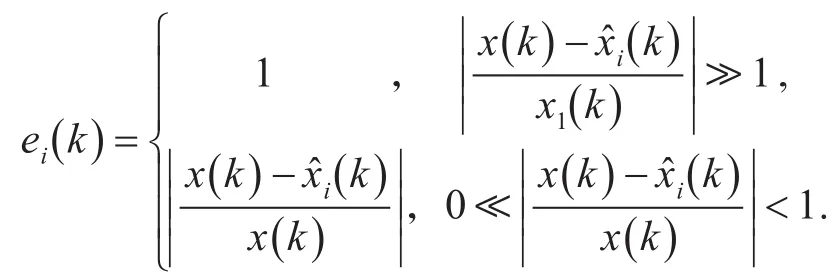
根据熵值法确定权重的步骤如下。

1）归一化单项预测方法的相对误差为

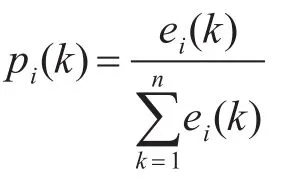
2）计算单项预测模型相对误差的熵值为

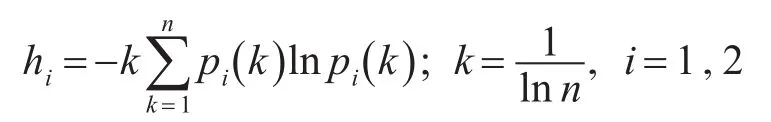
3）计算单项预测模型相对误差序列的变异程度系数为

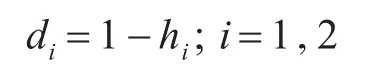
4）计算单项预测模型的加权系数为

5）将各单项模型的信息熵权重系数加权求和，则组合预测模型为

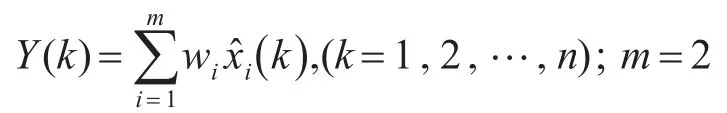
3.2 模型的精度检验与分析

为分析预测模型在沉陷监测间断数据插补中的应用，采用平均相对误差检验和后验差检验法进行精度检验。预测模型的残差序列E计算为

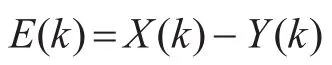
式中，X为实测值，Y为预测值。

平均相对误差为

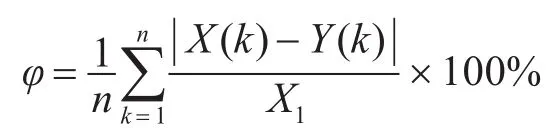
原始序列和残差序列的方差为

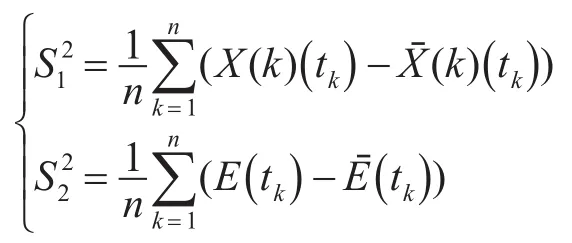
式中，。

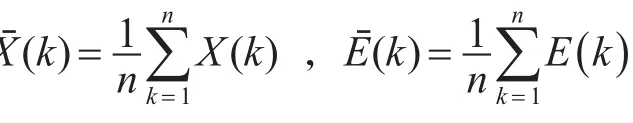
其后验方差比为

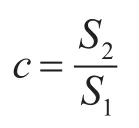
小误差概率为

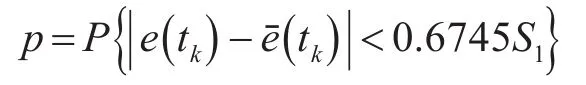
根据c，p值将预测模型预测精度分为4个等级，可综合评定灰色GM（1，1）模型预测精度，见表1。

表1 模型精度检验等级参照表

4 实验分析

以某矿区22001工作面上的监测点高程数据为例，其工作面走向长430m，且达到充分开采。该工作面沉陷监测采用导线测量和水准测量方法，对沿铁路轨道布设的监测点进行观测。由于诸多因素的影响，导致矿区地表的观测数据出现间断缺失，而为了研究矿区地表沉陷规律，需对间断部分数据进行插补。选取22001工作面上10期观测数据，其中监测点k1+935在4月8日-5月4日之间有3期数据缺失，本文选取附近三个观测站k1+885、k1+910、k1+960的监测数据对其进行预测插补。其观测数据见表2。

表2 矿区沉陷监测点高程数据

4.1 沉陷监测间断数据插补

将k1+935的监测数据与k1+885、k1+910、k1+960的监测数据按式（1～3）进行灰色关联度分析计算，得出灰色关联度分别为0.68、0.66、0.75，三个监测点与k1+935的关联度都大于0.6，表明三个监测点观测数据与点k1+935的监测数据关联性强，可根据灰色GM（0，N）模型与Elman神经网络模型原理进行建模。则k1+935的间断插补值及精度见表3。

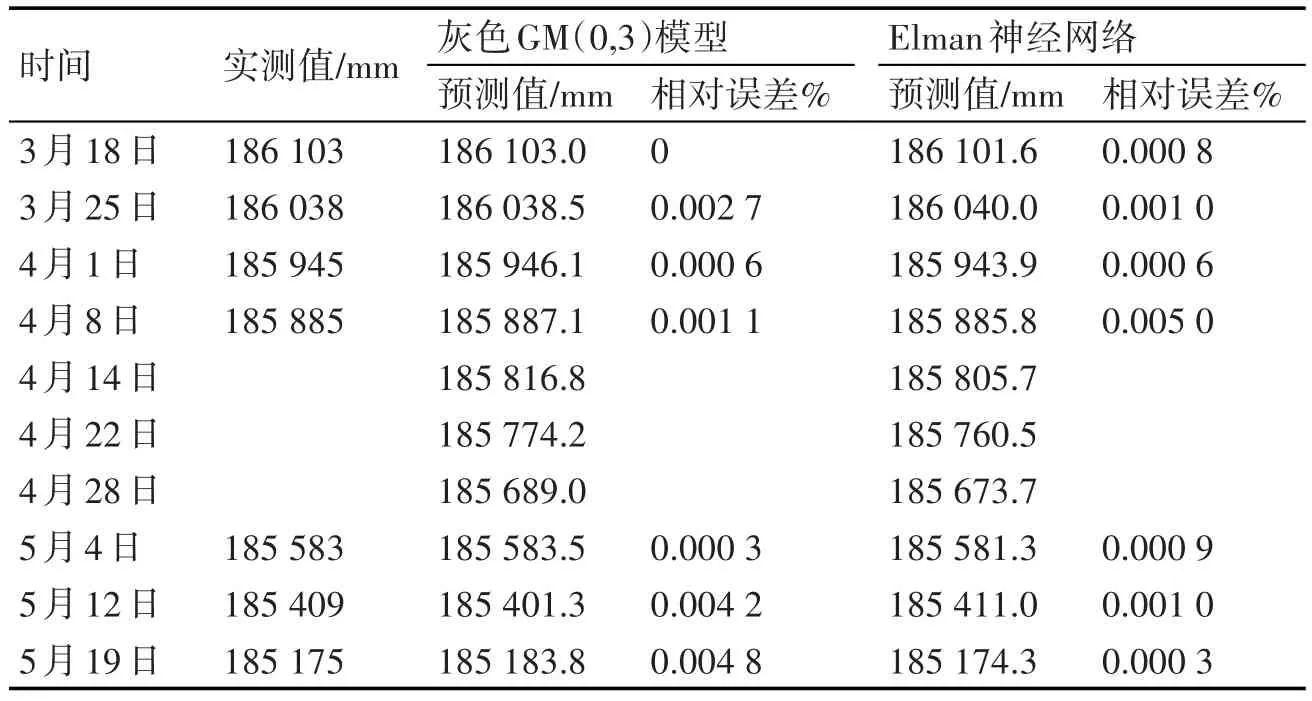
表3 灰色GM（0，3）与Elman神经网络间断插补值

将灰色GM（0，3）模型与Elman神经网络模型的拟合值应用熵权法确定组合权值，然后根据组合权值确定灰色神经网络组合模型的间断插补值，其组合模型预测结果见表4。

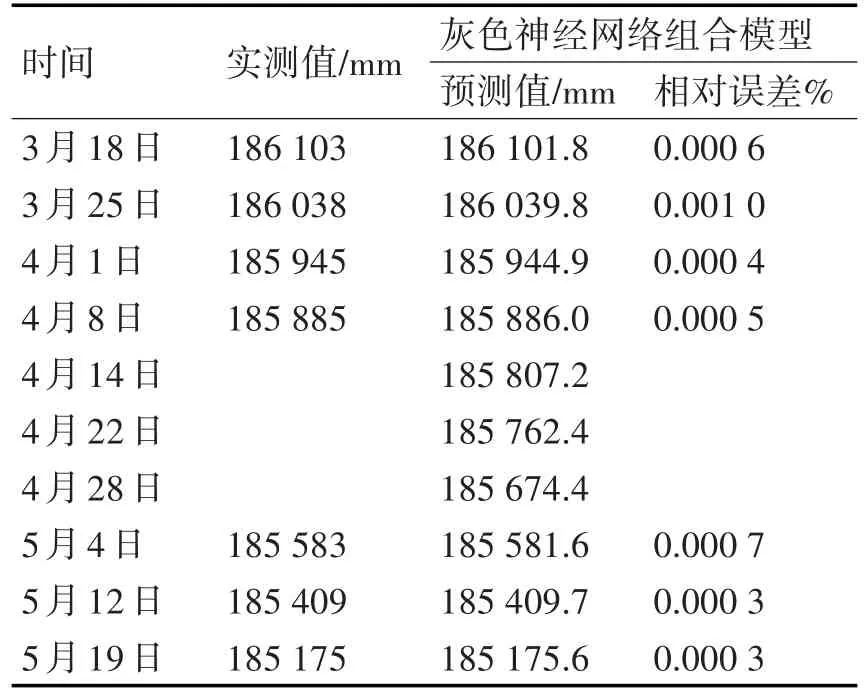
表4 灰色神经网络组合模型间断插补值

由表3、表4数据计算可知，灰色GM（0，3）模型平均相对误差为0.001 9，Elman神经网络模型相对误差为0.001 3，灰色神经网络组合模型相对误差为0.000 5，灰色神经网络组合模型的拟合精度优于单项预测模型拟合精度，对沉陷监测间断的插补数据应更接近于实测值。

4.2 模型精度检验

将表3、表4中的数据按平均相对误差与后验差检验法进行计算，实测值的均方差为249.079 9，Elman神经网络、灰色GM（0，3）模型及其组合预测模型的残差的均方差分别为1.562、3.249 8、1.208 9，则预测模型的精度统计见表5。

表5 预测模型的精度统计

由表5知，各预测模型的精度检验均为一级，都可应用于沉陷监测间断插补。但是组合模型的拟合精度最高，沉陷监测间断插补精度应高于单项预测模型。

5 结语

1）通过灰色关联度分析确定与点k1+935关联性强相邻测点的监测数据，采用灰色GM（0，n）模型与Elman神经网络模型进行拟合与预测，结果点k1+935的监测数据拟合精度为一级，则应用灰色GM（0，n）模型与Elman神经网络模型对间断部分插补是可行的。

2）将这两种单项预测模型进行组合建立灰色神经网络组合模型，其拟合精度高于单项预测模型，表明组合模型对沉陷监测间断插补是有效的，能发挥各单项预测模型的优势，能较好地反映地面沉陷的变化趋势，为沉陷监测间断过程的沉陷变化规律的研究与分析提供可靠的数据资料。