多层热防护服一维瞬态导热优化模型

朱家明，左正东，杜佳轩，王浩歌

（1.安徽财经大学 统计与应用数学学院，蚌埠 233030；2.安徽财经大学 金融学院，蚌埠 233030）

大量的科学统计研究表明，高温极端环境会使暴露其中的工作人员发生中暑等症状，各地方政府推出了“高温限工令”，即规定气温超过35℃的，要避免11：00-15：00室外露天和高处作业，此项举措对保护工作人员的健康和权益方面有一定的积极作用［1］。体表温度作为人体生理指标之一［2］，在室内热环境学、生理学等领域有着重要的研究意义。通过探究多层热防护服一维瞬态导热规律，在生产设计高温热防护服方面有一定的借鉴意义。

数据来源于2018年高教杯全国大学生数学建模比赛A题，为了便于解决问题，提出了如下假设：（1）无内热源且初始温度均匀分布；（2）材料成本与厚度成正比；（3）热量传递的方向视为一维垂直于皮肤表面辐射；（4）热防护服装的织物各项指标性质相同；（5）该模型仅考虑热传递；（6）传导和辐射在织物中热传递是均匀的；（7）防护服最外层和人体皮肤传递过程中的辐射可以忽略；（8）空气层的厚度值不超过6.4mm（忽略热对流影响）；（9）织物与织物间，织物与外界空气间，空气与人体皮肤之间的温度变化连续的且梯度跳跃。

目前关于热防护服内部传热模型根据热防护服材料层数分为单层和多层模型。单层热防服模型只有外壳，国内外学者主要研究外界环境的辐射热量、织物性质、空气层厚度对防护服热性能的影响［3］。Gibson［4］首先提出高温单层多孔介质传热传质模型，Torvi［5］考虑不同辐射强度对热防服内部热传递的影响。Ghazy［6］利用单层织物中热传导及比热采用经验公式，将常量转为变量，更好地拟合了高温情况的热传递过程。

许多学者在单层模型的基础上改进并探究了热防护服热湿传递多层模型。Mell［7］提出了多层面料模型层与层之间的传热模型。Mercer［8］和Ahmed Elgafy［9］考虑到由于相变材料对防护服的热防护效果的影响，建立了内含相变材料的多层动态热传递模型。

1 基于傅里叶定律和COMSOL仿真模型对温度分布的计算

1.1 研究思路

首先分析单层无限长圆筒温度分布的一般情况。以此为基础进一步探讨一维平板稳态线性变温导热率的情况下的温度分布，根据边界条件引出四种组合，再建立非线性方程组，通过求解雅克比矩阵，并使用牛顿迭代法求解，给出温度位置分布函数。考虑到不同层厚度差异较大，同层不同厚度的位置其温度存在着差别，为了更加准确地计算温度分布状况，将层数进行进一步细化，利用COMSOL软件进行仿真，得到各个厚度位置的每秒具体的温度值，可以直观地看出传热过程。织物厚度越厚，隔热效果越好，皮肤表面温度也越低。对第II层进行扫描。改变第II层和第IV层的厚度时，从节约材料的角度考虑，应该尽可能减少第II层的厚度，增大第IV层的厚度，以达到相同的效果。首先固定第II层的厚度，改变第IV层的厚度。最大的第IV层厚度的同时也须保证第II层厚度最小，此时为最优值。

1.2 模型的建立与分析

1.2.1 温度的时间空间分布

为了简化问题，假设人为半径220mm，高1700mm的圆柱，当人穿着防护服时，在柱坐标系下类似于多层圆筒壁（见图1），一维非稳态导热实际上是二维问题，需要考虑时间（单向）和空间坐标。

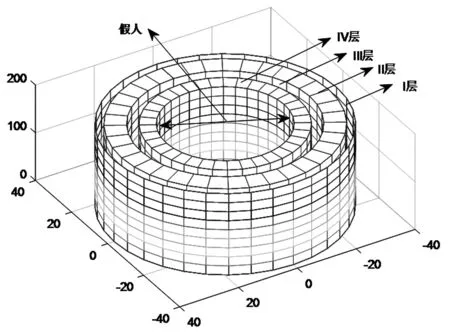
图1 假人高温作业专用服装穿着仿真图

在图1中给出了由服装——皮肤及空气层组成的系统，其中，防护服通常由三层织物材料构成，记为I、II、III层，其中I层与外界环境接触，III层与皮肤之间还存在空隙，将此空隙记为IV层。

从外到内，织物距离皮肤的距离以次为d1、d2、d3，材料的热传导率以次为k1、k2、k3，表面温度值以次为T1、T2、T3、T4。如图2所示。

图2 多层结构温度分布边界结构简图

其中T1=75℃，T5=37℃ ，d2-d3=6mm ，d4-d5=5mm。

导热系数的计算式是由傅里叶导热定律的数学表达式导而出，即：

导热系数是表示物质导热能力的大小的一项基本宏观物理性质。本题中导热系数被当作常数对待。大部分情况下，导热系数与温度呈非线性关系的。通常在实际计算中，若温度变化范围不大，其数值可近似采用线性关系，即

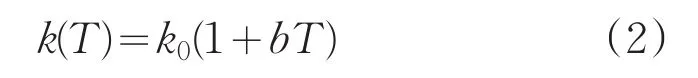
式中，T为温度，b代表该温度范围内导热系数随温度的变化，其值为常量，b＞0时热导率与温度成正比，b＜0时热导率与温度成反比，b=0时热导率是常数［10］。

下式中的系数Ai、Bi等值为由边界条件确定的系数。

由题可知，两层织物的热流密度相等，即

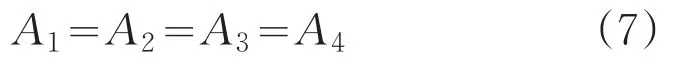
由式（3）、（4）、（5）、（6）整理得：

方程（9）是一个关于中间界面温度T2、T3的非线性方程组，可用牛顿法解出：

雅克比矩阵为：

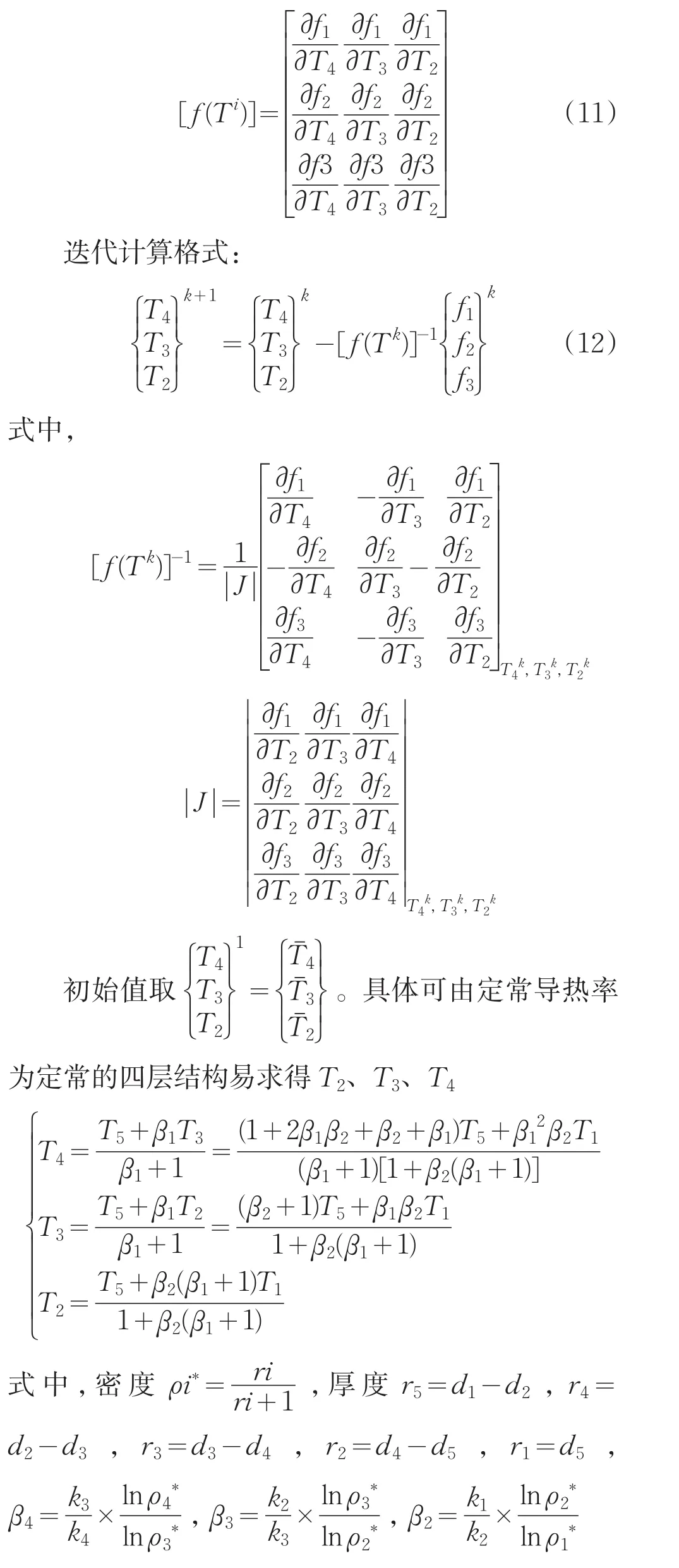
代入（11）迭代，可求得T2、T3、T4，然后计算温度分布等。

第IV层温度分布：

考虑到不同层厚度差异较大，同层不同厚度的位置其温度存在着差别，在（13）-（16）式的基础之上，为了更加准确地计算温度分布状况，将层数进行了进一步细化，选取了52个节点，将0～15.2mm的厚度划分为了51个细微厚度层，在厚度层内，温度基本无差异。而多层圆筒壁导热的一维问题，在垂直导热的假设前提下，可以进一步简化为图3，图3从左到右衡量分别为I、II、III、IV层，且在51个区间内每秒温度存在着瞬时变化，每个区间的垂直圆筒壁的温度在每一秒下是相等的。

图3 一维简化仿真图

利用COMSOL软件进行仿真，可以得到各个厚度位置的每秒具体的温度值，将其绘制为温度随厚度与时间变化的三维立体图（图4），可以更直观的看出传热过程，导热进行50秒后，初始条件37℃对系统中无量纲分布的影响趋近于0，温度分布此时主要取决于第三边界条件的影响。其在1100mm时基本达到稳态，温度基本保持稳定。温度时间分布误差分析如图5所示。

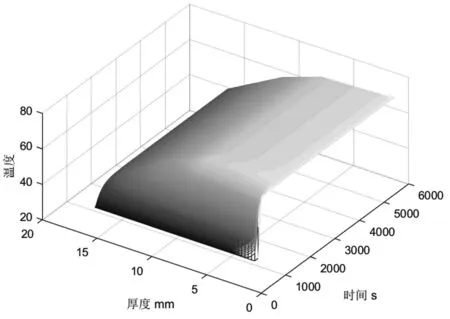
图4 温度厚度时间三维坐标系图

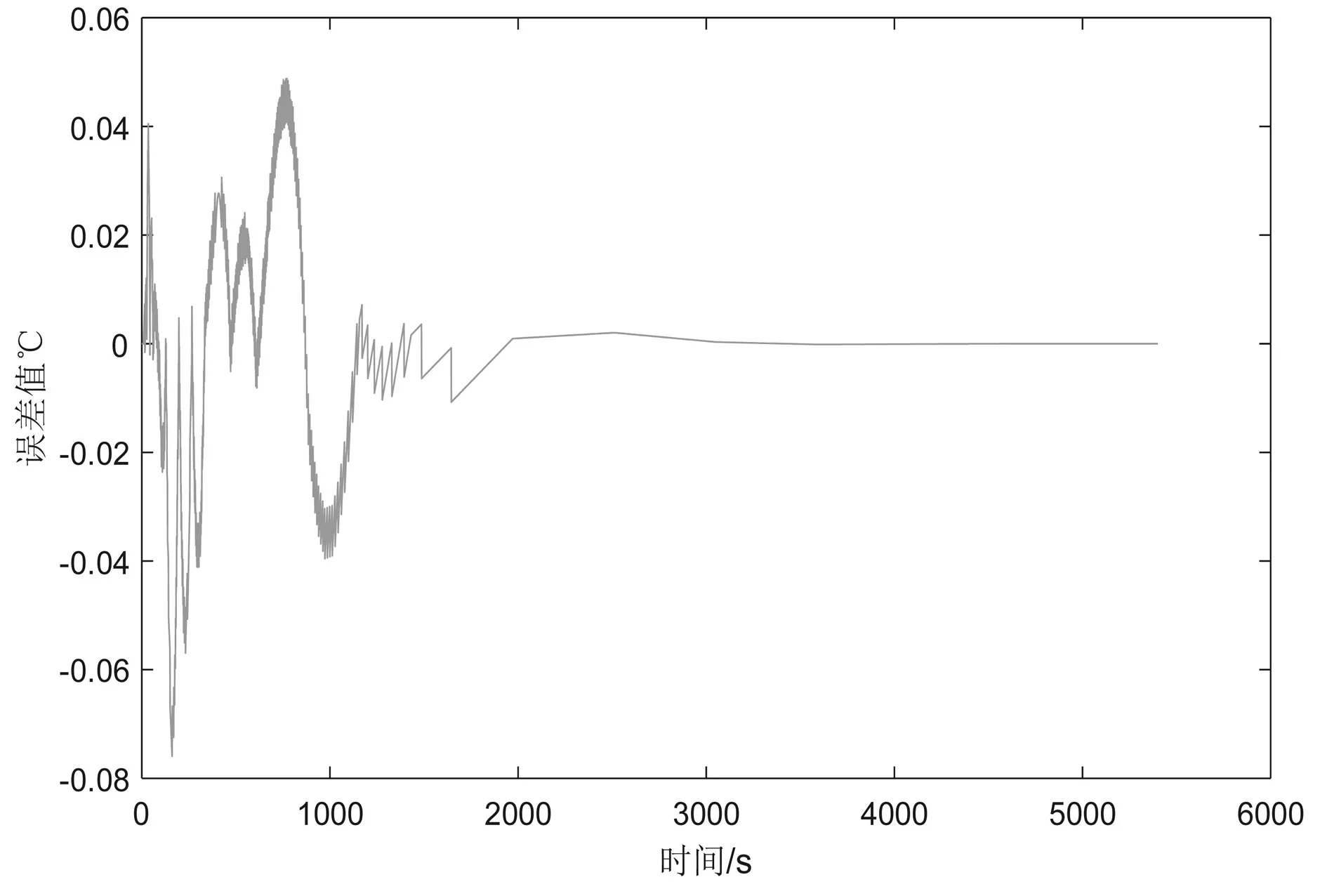
图5 温度时间分布误差分析图

将所得到的假人皮肤外侧的实时温度值（即厚度为15.2mm处）与数据中给的测定值进行比较（见图6），可以看出本模型的热传导预测效果较好，基本吻合实测值，只在1000秒到1500秒之间略有偏差，因此本模型准确度较高。

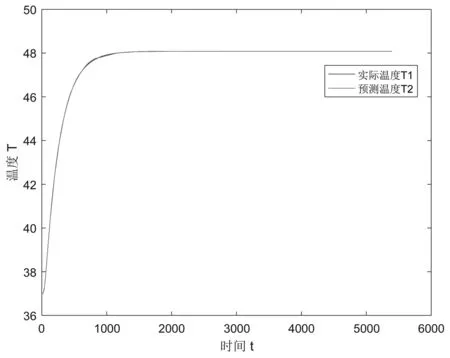
图6 预测温度与实际温度差值相关图

再利用MATLAB绘制三维等温线图（见图7），在三维空间内的同一等温线上温度相等，到达稳态的实际根据厚度的不同而变化。

图7 空间直角坐标材料三维等温线分布图

利用COMSOL Multiphysics软件的一维瞬态无内热源导入公式（17）（18）：

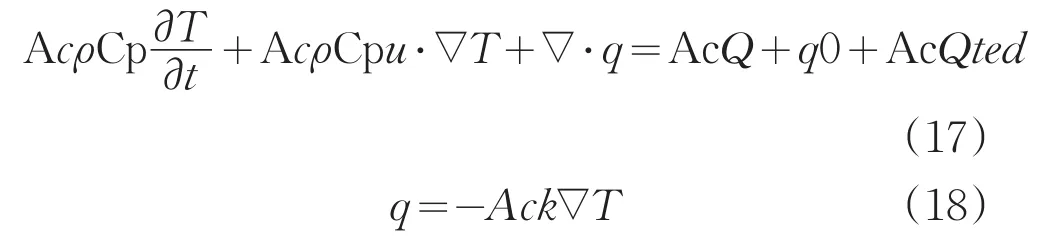
以上是热传导方程，Ac是一维线的横截面积，ρ是密度，Cp是比热容，T是温度，t是时间，u是速度，固体不流动，不用考虑。k是导热系数。等式左边第一项代表材料温度改变，第三项代表热传递贡献，等式右边是热量产生，在本模型种并没有热量生成，不需要考虑。

1.2.2 基于温度分布曲线对防热服厚度的最优设计

织物厚度越厚，隔热效果越好，假人皮肤外侧温度也越低。

利用之前的函数：

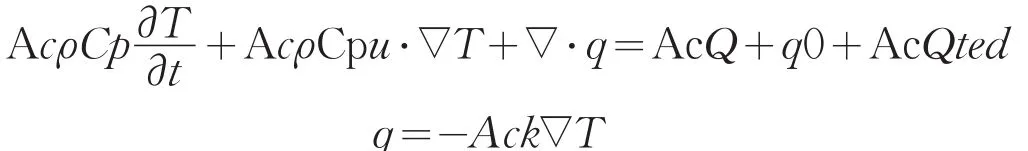
利用局部差分法，对该方程进行二次积分，求出温度分布的函数：

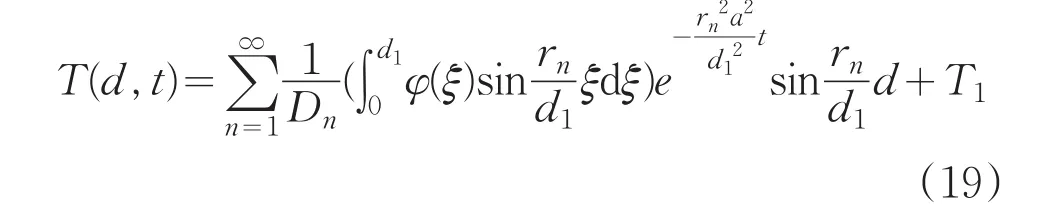
若要求在确保工作60分钟，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5分钟的情况下，确定第II层的最优厚度。最优厚度即为满足上述约束条件下的该层最薄厚度，这样节省材料费用，达到最优，即为求min（d2-d3）。约束条件为：

其中，t(T,d)为T(t,d)的相关函数。

1.3 模型结果及分析

在其他变量不变的情况下，在第II层厚度的取值区间内，不断变换第II层厚度，得到不同厚度下的假人皮肤外侧实时温度分布状况绘制如图8所示。

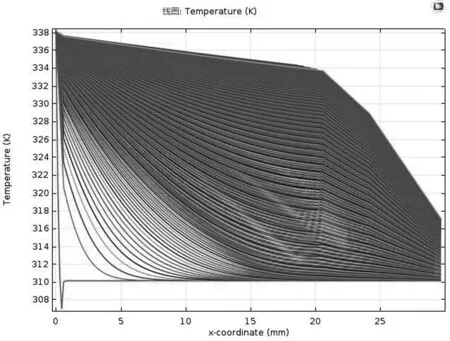
图8 假人皮肤外侧温度分布曲线图

结果发现当第II层厚度达到19mm时，在55分钟时，温度达到44度，并且在60分钟时，温度也只是稍微高于44度，达到临界值，此时的温度分布曲线如图9所示。

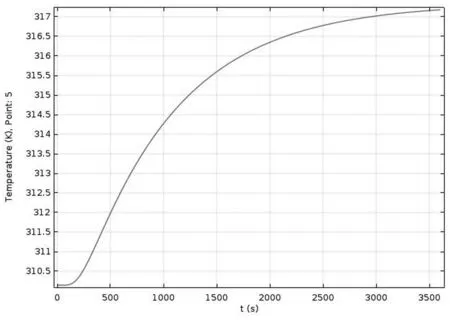
图9 假人皮肤外侧温度分布曲线图

为考虑节约材料，最优厚度应该定位在稍厚于19mm的19.5mm。

表1是当第II层厚度为19.5mm时，部分时间的温度（单位为开尔文）变化。

当第II层和第IV层的厚度时可以改变的，从节约材料的角度考虑，应该尽可能减少第II层的厚度，增大第IV层（该层为空气层）的厚度，以达到相同的效果。首先固定第II层的厚度，改变第IV层的厚度。假设固定第II层为10mm，逐渐增加第IV层的厚度，通过COMSOL Multiphysics软件扫描发现当第IV层厚度达到最大值6.4mm时依然不满足确保工作30分钟时，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5分钟的条件。具体温度变化如图10所示。

图10 固定第II层厚度改变第IV层厚度的温度变化线图

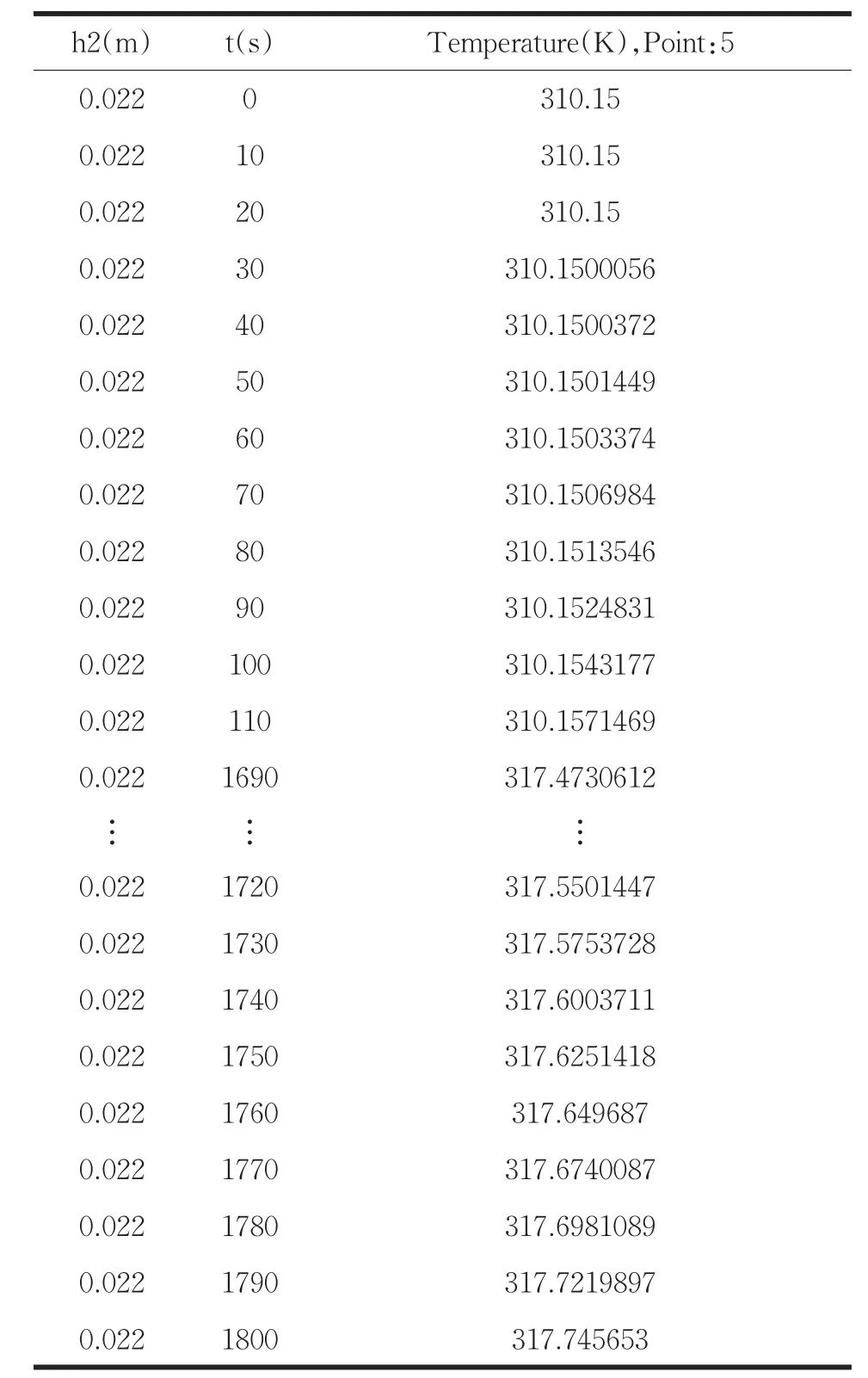
表1 假人皮肤外侧温度随时间变化一览表

因此逐渐增加第II层厚度，使得第IV层厚度在最大值6.4mm时，满足要求条件。最大的第IV层厚度也保证第II层厚度最小，从而达到节约材料的目的。具体温度变化如图11所示。

结果发现当第II层厚度为22mm，第IV层厚度为6.4mm时，满足要求条件，为最优值，温度曲线如图12所示。

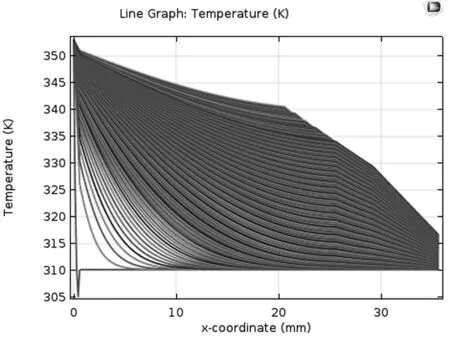
图11 固定第IV层厚度改变第II层厚度的温度变化线图

图12 第IV层、第II层最优厚度的温度变化线图

2 结论

基于传热学的理论，对不同假设下、不同初始条件、以及不同形式的存在耦合关系的多层圆筒体模型进行探究，以界面温度为解耦参数，将多层传热简化成单层传热问题，从而推导出多层圆筒体在不同边界条件下的温度分布表达式。通过借助COMSOL 5.3a软件，以有限元法为基础，通过求解偏微分方程来实现真实导热现象的仿真，将复杂的多层圆筒壁瞬态导热模型进行简化，大大降低了计算难度。文中建立的模型与紧密结合实际情况，突出了传热系数的作用，充分考虑物理学原理，从而使模型更加通用、易懂。