基于ABAQUS二次开发变角度层合板屈曲特性分析
年春波 王小平 代文猛 杨 洋
(南京航空航天大学机电学院,南京 210016)
文 摘 基于ABAQUS二次开发,探究周期函数曲线纤维路径变角度复合材料层合板的屈曲特性。首先,以正弦曲线为基本参考路径为例,得到纤维角度的变化规律;然后,利用Python编写变角度复合材料层合板的有限元分析前处理程序,开发出ABAQUS交互式界面;最后,利用本文开发的GUI插件,对经典定角度和变角度层合板进行屈曲分析。结果表明,变角度层合板的屈曲载荷有很大提高,并且随着幅值参数A和周期参数T逐渐增大,一阶线性屈曲均是呈先增大后减小的趋势,因此基于铺层稳定性,参数应控制在相应的范围。采用Python对ABAQUS进行二次开发,从而实现变角度层合板的自动建模和计算分析,为实际工程研究提供了研究思路和流程,有一定的实践意义。
0 引言
先进复合材料因其质量轻、耐疲劳、强度高、抗腐蚀等优点,被广泛用于航空、航天等高科技领域[1]。复合材料不仅减轻了飞机的结构质量,还提高了飞机结构的使用寿命[2]。随着我国大飞机项目的启动,复合材料成型技术的研究也越来越紧迫,优化复合材料性能改进成型技术的效率是研究复合材料的重中之重。
经过半个多世纪的发展,纤维增强复合材料层合板由传统的直线铺放形成复合材料层逐渐向变角度曲线铺层过渡。Z.GÜRDAL等[3-4]提出了纤维铺放角线性变化来形成曲线纤维路径,引出了变角度纤维铺放概念,并将变角度铺层应用到实践中。C.S.LOPES[5]对变角度层合板进行有限元计算,对其进行屈曲载荷分析和首层失效分析。A.W.BLOM[6]对圆柱和圆锥类结构进行变角度轨迹规划、并对铺层进行了静力学和动力学特分析。Z.M.WU等[7]提出一种新的数学定义模型描述纤维的铺放轨迹,研究选取Rayleigh-Ritz法来确定预屈曲载荷和临界屈曲载荷的分布,并且以屈曲载荷最大为目标对纤维铺放角进行了优化。H.AKHAVAN[8]则对线性铺放角的变角度层合板进行自然频率和振动模态分析研究。研究表明,复合材料层合板的固有频率和阵型随着铺放角改变而相应的改变。
在国内,董文武等[9]应用ANSYS软件对复合材料锥形壳体进行有限元分析并对其进行轴压实验,通过对比建立了有限元分析和实验研究的关系。罗翔鹏[10]等在ANSYS中分析了带有圆孔的复合材料板料的力学状态。马永前[11]等采用纤维角度线性变化的铺层,对层合板进行有限元建模分析,验证了在面内受力的情况下,屈曲荷载显著提高。李玥华[12]研究了管状零件变角度轨迹规划算法,并对锥壳零件进行有限元建模,并对铺层进行静力学、模态及线性屈曲分析。马洪涛[13]通过模拟分析,研究了变角度层合板的力学性能,并且给出了最佳曲线铺设方式和铺设角度。富宏亚等[14]提出了分段式二次Bezier曲线变化方法,并以此来定义纤维铺放参考路径,研究了曲线不同终止角和连接点参数对复合材料层合板屈曲特性的影响。目前,对于层合板纤维曲线路径描述比较局限,还未见对周期函数曲线纤维路径进行研究。周期函数相较之前的曲线路径,有更大的可控性,通过控制周期函数的周期、相位等参数,能灵活的改变曲线的形状。本文以正弦曲线为例定义纤维铺层,研究曲线纤维角度的变化规律,并利用Python脚本开发了可应用的ABAQUS GUI插件,探究不同振幅A和周期T对复合材料层合板屈曲特性的影响。
1 变角度复合材料层合板设计
在设计复合材料铺层时,首先应该确定参考路径,然后对参考路径进行等距(平移法或平行法),从而可以得到整个铺层的纤维轨迹。本文主要思路为:通过研究纤维曲线的轨迹,得到曲线角度的变化规律,从而建立有限元前处理模型。
假设参考路径通过层合板中心,正弦曲线纤维参考路径如图1所示。
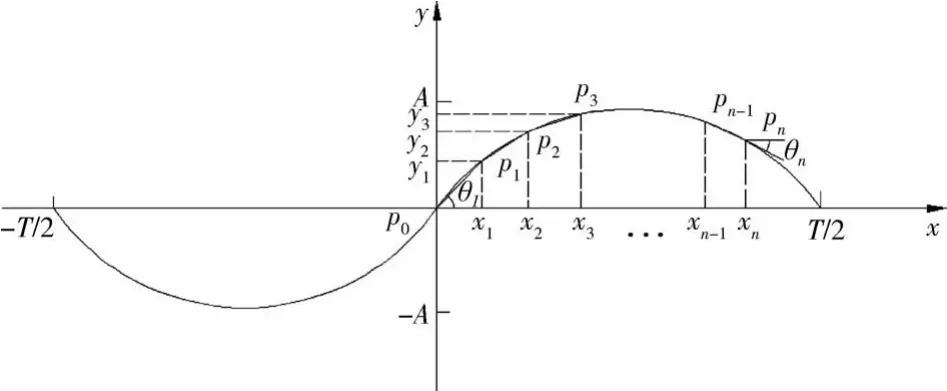
图1 正弦曲线纤维参考路径Fig.1 Sinusoidal fiber reference path
由于曲线关于层合板中心对称,所以曲线角度也关于层合板中心对称,因此只研究曲线的右半部分,曲线路径的表达式为:
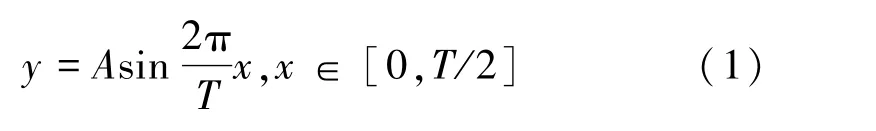
式中,A为正弦曲线的振幅,T为正弦曲线的周期。由于后期有限元建模过程中,需要对平板进行网格化处理,故将正弦曲线进行离散,得到一系列离散点p0、p1、p2…pn,将曲线角度定义为:

从角度的数学描述来看,影响参考路径的主要参数为A与T,由于改变A与T,层合板的结构会发生变化,故将纤维曲线铺放变角度复合材料层的表示方法为[φ<A/T>](φ为旋转角度)。图2为铺层示意图。
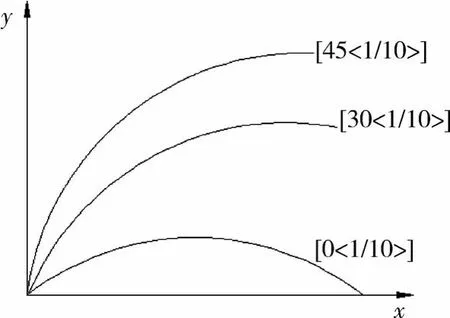
图2 参考路径铺层示意图Fig.2 Schematic diagram of the reference path layer
为了得到更一般的纤维路径,可以通过旋转纤维变化的坐标轴来实现,如图3所示,逆时针为正。

图3 任意坐标系下的参考路径Fig.3 Reference path in a arbitrary coordinate system
根据坐标变换公式可得:

式中,φ为旋转角度,逆时针为正;θ为(x,y)坐标系下的纤维角度;θ′为(x′,y′)坐标系下的纤维角度。
与之前的曲线路径比较,周期函数曲线控制更为灵活,图4为不同周期和不同振幅下的参考路径。通过控制参数A、T可以使角度发生非线性变化,图5为层合板[0<2/10>]参考路径角度变化规律。对曲线进行旋转与拼接,正弦曲线可以近似逼近于直线和线性角度法,故基于正弦曲线的纤维路径相较传统的路径设计有很大的可控制性,通过双参数A、T进行设计路径,设计过程更为灵活。为了得到整个铺层的路径,通常需要对参考路径进行平移等距或平行等距,本文采用平行等距方法,图6所示为层合板[0<1.5/10>]铺层示意图。
整体总结而言,2018年家电业上市公司普遍面临业绩下行的压力,行业整体表现不佳。除格力、美的、海尔三大白电企业因空调、冰箱、洗衣机市场集中度较高而逆势增长外,其它传统品类增速下滑,彩电、厨电、显示面板企业的业绩多数同比降减;专业品牌和品类单一的企业受到的销售压力更大,新兴产品表现也不及预期,尤其与地产关系接近的厨电、燃热、洗碗机等品牌表现更为逊色些。
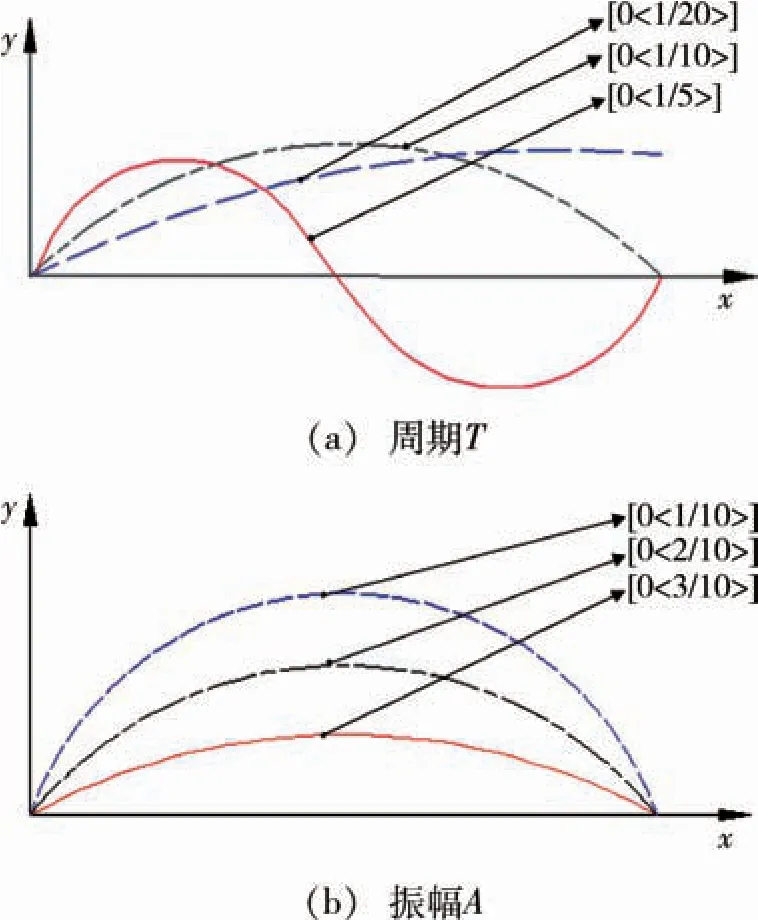
图4 参数对参考路径的影响Fig.4 Influence of parameters on the reference path

图5 层合板[0<2/10>]参考路径角度变化规律Fig.5 Reference path angle change law of laminates[0<2/10>]

图6 层合板[0<1.5/10>]铺层示意图Fig.6 Layer diagram of laminates[0<1.5/10>]
2 变角度复合材料层合板建模
2.1 有限元前处理模型的建立
本文采用的正弦曲线为参考路径,其纤维铺放角随层合板的位置不同而不断变化。然而对于目前有限元计算软件来说,都还只能处理固定角度的直线铺层,对不断变化角度的曲线铺层,有限元软件不能直接处理。因此在有限元处理前,要进行一定的前处理,处理思路为:首先对变角度层合板的整个铺层离散成很小的单元,然后将曲线以网格为单位进行离散,在每个网格内部“以直代曲”,给每一个小单元分别赋予层合板材料属性,在每个小单元内,纤维角度可以被视为定值。上述有限元建模需要借助ABAQUS二次开发接口Python来完成。本文选用的层合板模型为100 mm×100 mm复合材料层合板,所使用的复合材料参数见表1。

表1 预浸丝材料参数Tab.1 Parameters of prepreg material
为了分析层合板的力学性能,需要对模型施加边界条件及载荷。本文将平板的左边限制其x、y、z方向的位移,在上下两边限制z方向的位移,在平板的右边约束其y、z方向的位移并在x方向施加100 N/mm压缩载荷,如图7所示为有限元模型的边界约束与载荷显示。

图7 层合板有限元模型的边界约束与载荷Fig.7 Boundary constraint and load of the finite element model of laminate
2.2 GUI插件的开发
本文ABAQUS插件通过Really Simple GUI(RSG)Dialog Builder设计得到。RSG插件编写工作分为两部分:一部分是对话框编辑,这部分是用于从用户处收集参数;另一部分是编写Kernel函数,该函数就是我们需要插件完成的工作,它接收来自GUI对话框的输入信息并执行相应的功能。如图8为RSG GUI编辑界面。
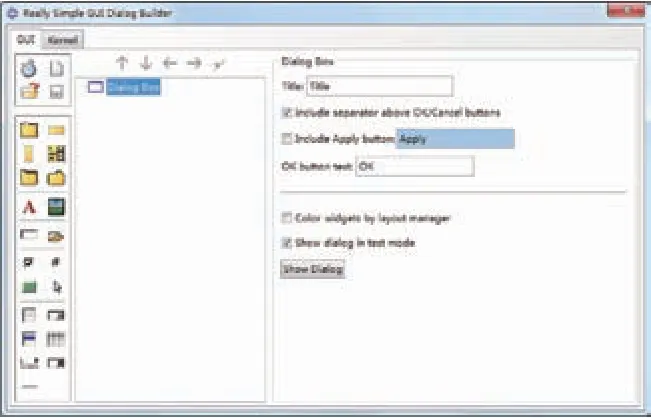
图8 RSG GUI编辑界面界面Fig.8 RSG GUI editing interface interface
插件的功能为输入需要设置的幅值参数A和周期参数T,进行ABAQUS的前处理和提交计算,而后提取所需结果。本文研究路径参数对屈曲的影响,因而开发了插件Variable Angle Laminates(VAL)_Buckle(变角度层合板屈曲分析),图9为所开发GUI插件,图10为程序设计流程。

图9 GUI插件Fig.9 GUI plug-in
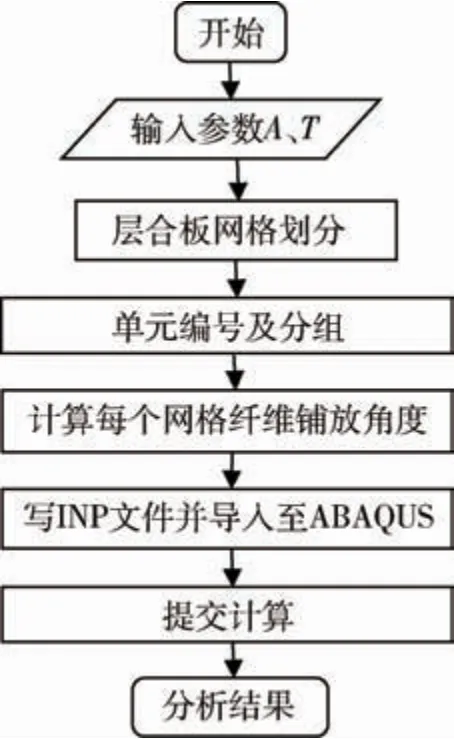
图10 GUI程序分析流程Fig.10 GUI program analysis process
3 复合材料层合板线性屈曲分析
3.1 经典定角度复合材料层合板线性屈曲分析
对经典定角度直线铺层进行屈曲分析,得到的一阶线性屈曲载荷如表2所示。

表2 定角度层合板一阶线性屈曲载荷Tab.2 First-order linear buckling load of fixed angle laminate
3.2 变角度复合材料层合板线性屈曲分析
3.2.1 曲线幅值A对变角度层合板屈曲的影响
为了探究曲线幅值A对层合板屈曲的影响,控制T保持不变,通过改变A,将参数输入本文所开发的插件中,得到层合板一阶屈曲载荷,如表3所示。其中铺设方式采用前文所定义的表示方法[φ<A/T>]s,φ为旋转角度,s是symmetry的缩写。因考虑曲线曲率过小时,铺丝会出现褶皱现象,因此A没有取得很大,探究范围为1~10 mm,本文主要探究参数A、T对屈曲的影响,故坐标系的旋转角度均为0°。

表3 变幅值层合板屈曲分析Tab.3 Buckling analysis of variable amplitude laminates
为进一步探究A对层合板屈曲性能的影响,将表3绘制如图11曲线。可以看出,通过改变A,层合板屈曲载荷会发生明显的变化,当A为1~3 mm时,屈曲载荷较大,并且大部分高于经典定角度铺层,在进行的仿真实验中,铺层[0±2/15]2s屈曲载荷最大,达到了791.37 N,因此达到了仿真实验的目的。由图10可以明显看出,在可控范围内,无论T取多大,屈曲载荷随着A的增大,都是先增加后减小,并且在A=6 mm之后,相同的A,T越大屈曲载荷越大。因此在层合板设计时,幅值A是重要的影响参数,通过提高幅值A,可以提高层合板的稳定性。图12为T=10 mm,A从1~10 mm层合板一阶屈曲模态,可以看出,由于A的变化,模态发生了变化。
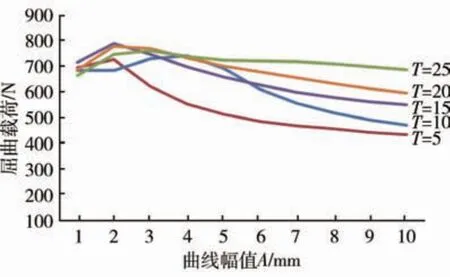
图11 不同参数A的复合材料层合板一阶屈曲载荷Fig.11 First order buckling load of composite laminates with different parameters A

图12 不同参数A层合板一阶线性屈曲模态Fig.12 First order linear buckling modes of laminates with different parameters A
3.2.2 曲线周期T对变角度层合板屈曲的影响
探究参数T对变角度层合板线性屈曲载荷的影响。如表4所示,通过改变铺层设计的周期参数T,探究变角度层合板线性屈曲载荷的变化。因考虑曲线曲率过小时,铺丝会出现褶皱现象,因此曲线幅值T没有取得很小,探究范围为5~95 mm。

表4 变周期层合板屈曲分析Tab.4 Buckling analysis of variable period laminates
为进一步探究T对层合板屈曲性能的影响,将表4绘制如图13曲线。
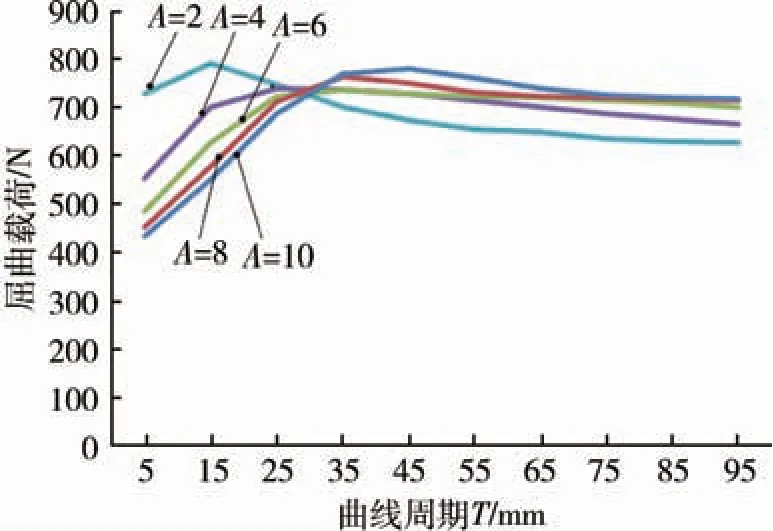
图13 不同参数T的复合材料层合板一阶屈曲载荷Fig.13 First order buckling load of composite laminates with different parameters T
综合表4和图13可以看出,随着T的增加,屈曲载荷都呈先增大后减小,而后平稳的趋势。T在15 mm之前,曲线斜率较大,T对屈曲载荷的影响较大,T在35 mm之后,曲线趋于平稳,斜率较小,T对屈曲载荷的影响较小。比较各曲线的值可以得到,T在25 mm之前,随着A的增大,屈曲载荷不断减小。因此,仿真结果表明,若想提高层合板的稳定性,应尽量控制T的范围。
4 结论
(1)研究周期函数曲线路径对复合材料层合板屈曲特性的影响,以正弦曲线为基本参考路径,得到了纤维角度的变化规律,通过改变幅值参数A与周期参数T对曲线进行调整控制,设计过程相较传统的路径设计有很大的可控制性;本文将曲线以网格为单位进行离散,在每个网格内部“以直代曲”,利用Python编写了变角度复合材料层合板的有限元分析前处理程序,并开发了ABAQUS交互式界面。
(2)基于本文开发的GUI插件,对经典定角度和变角度层合板进行屈曲分析,得到了层合板一阶线性屈曲载荷。综合来看,变角度铺层的一阶屈曲载荷大于直线铺层,并且通过控制参数A和参数T的变化可以得到稳定性较好的复合材料层合板。
(3)周期函数可设计性较强,通过控制参数,可设计成符合铺丝标准的路径,本文初步探讨了周期函数曲线路径层合板稳定性,对实际的工程有一定的指导意义。但在实际的工程应用中,路径和复合材料构件都较为复杂,本文采用Python对ABAQUS进行二次开发,从而实现自动建模和计算分析,为实际工程研究提供了研究思路和流程,有一定的实践意义。

