橡胶坝坝体振动模态特性及防治措施
任钟刚
(菏泽市黄淮水利设计咨询有限公司,山东 菏泽 274000)
橡胶坝通常采用高强纤维布作为受力骨架,外接硫化橡胶层进行止水后向内冲入气体或液体,从而形成橡胶柔性挡水体,在我国水利工程尤其是小型水利工程建设中起到不可或缺的作用。本文以山东省某拟建橡胶坝工程为例,通过ANSYS建立流固耦合条件下的橡胶坝坝体模型并进一步分析其振动模态特性与变形破坏特征,以求为该工程的安全建设提供一定的理论依据。
1 流固耦合振动理论及模型建立
1.1 流固耦合振动理论
在不考虑阻尼的基本假设条件下,基于流固耦合理论进行橡胶坝坝体的振动模态分析时,流体对坝体结构作用时的自由振动方程为:

式中:Ms、Ks分别为结构的质量矩阵、刚度矩阵,U为节点位移矩阵,为加速度矩阵,Kfs为刚度矩阵,P为扰动压强。根据Navier-Stokes方程,可以进一步推出离散条件下结构动力学方程如下:

式中:Mf、Kf、Mfs分别为流体的质量矩阵、刚度矩阵及流固耦合质量矩阵。联合式(1)、(2)得流固耦合条件下系统的完整控制方程如式(3):
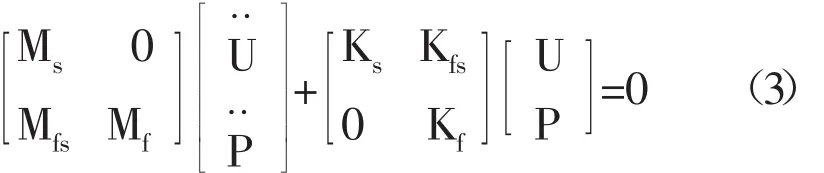
1.2 流固耦合模型建立
根据该橡胶坝工程相关资料及现场调查数据反馈,拟建橡胶坝尺寸为5.00m×15.18m,坝体及水体具体材料参数如表1所示。根据上述数据建立基于流固耦合理论的橡胶坝振动模态分析模型,坝体采用壳体单元SHELL63,水流采用流体单元fluid30。

表1 材料参数
橡胶坝袋的固定采用底板施加全约束堵头式锚固,根据上述相关参数,建立流固耦合条件下橡胶坝坝体模型,共划分为48956个单元。
2 计算结果分析
为充分预测在不同外界条件下橡胶坝坝体的运营状态,本次研究共对橡胶坝在不同内压比、不同高度下前10阶振型的自振频率及周期进行分析研究。高阶振型条件下振动图像及振动方向变得更加复杂,因此文中向平行水流方向,最大振动位移为1.08×10-4m;第2阶振型的主振方向为竖直向,最大振动位移为1.04×10-4m;第3阶振型的主振方向为平行水流方向,最大振动位移为6.38×10-5m;第4阶振型既有顺河向又有竖直向,最大振动位移为6.14×10-5m。由此可见,随着振动阶数的上升,橡胶坝坝体的最大位移不断减小,但在复合振动作用下发生大位移的点不断增多,破坏更加剧烈。
进一步探讨坝高对自振周期和基频的影响,设定内压比恒定为1∶3,分别设置坝高为2m、3m、4m、5m,并对4种不同坝高条件下的橡胶坝坝体自振频率及圆频率进行分析,可知,在流固耦合条件下,橡胶坝坝体自振频率、圆频率随着坝高的提升而下降,二者与坝高之间近似成指反比例关系,相关性系数分别达到R2=0.9947与R2=0.9943。分析认为,这是由于当橡胶坝坝高持续增长时,坝体的质量也随之不断增加,质量的增加使得坝体更加趋于稳定状态,因此自振频率与圆频率不断降低。
分析不同内压比条件下,橡胶坝体自振频率、圆频率随内压比变化的规律。预设内压比为1∶2.5、1∶3.0、1∶3.5、1∶4.0,分别计算 4 种内压比下橡胶坝的自振频率与圆频率,由坝体自振频率、圆频率与内压比关系曲线可知,流固耦合条件下橡胶坝坝体自振频率、圆频率也随着内压比的增大而不断下降,与坝高关系不同的是,自振频率、圆频率与内压比关系成线性关系而非反比例关系,相关性系数分别达到R2=0.9753与R2=0.9800,由此可见具有高度的相关性,充水式橡胶坝坝体在内压比增大时质量也会随之增大。
3 防治措施
1)在橡胶坝工程勘察设计选址阶段,为增强坝体的稳定性,应将坝址选择在直段两岸稳定的河段上;2)抬高坝袋基础底板,合理控制上、下游水面高度差;3)按照安全性、经济性原则设计合理的坝高,降低坝体自振频率;或在某确定坝高条件下,适当提高坝袋内压,使坝体“刚性”增强,从而减小了脉动荷载幅度,使坝袋不容易发生振动;4)在坝体上每3~5m距离预安装扰流器或差动式挑坎,破坏溢流水舌真空,避免坝体与水流发生共振现象。

