基于蚁群算法的农机混流车间配送路径研究
万 林,张志文,杨晓英
(河南科技大学 机电工程学院,洛阳 471003)
0 引言
农机装备生产受市场需求和国家政策影响较大,机型和配置更新换代速度快,农机装备需求针对性较强,针对不同地域、环境、作业需求都需要选配不同的机型,造成了生产转换快、动态性强等特点。随着市场竞争和客户个性化需求的加剧,多品种小批量的混流生产已经成为企业满足市场多样化需求、提高装配效率和加快企业响应速度的重要手段。多种机型共线装配造成了混流装配线工位需求随生产转换发生变化,造成配送路径难以规划的问题,传统企业一般采用大量储备线边库存的方法,造成了高昂的库存成本,因此对混流装配车间配送车辆的配送路径进行合理的规划,对企业降低库存和配送成本有重要意义。
近年来针对配送路径优化主要有以下研究,徐海宁、徐星[1]针对混流装配准时化配送,结合遗传算法改进蚁群算法,对模型求解。王力锋、杨华玲等[2]对最优网络路径选取,构建了车辆调度数学模型,实现配送路径最优化。针对复杂环境下路径寻找困难,王钦钊、程金勇、李小龙[3]采用基于势场优化的蚁群路径规划算法。赖智铭、郭躬德[4]改进了蚁群的回退策略,提出了二次优化,Rajappa G P,Wilck J H,Bell J E等[5]在标准路径规划问题上,对遗传算法和混合元启发式算法进行测试,寻找最优解决方案。以上学者的研究都实现了提高寻路的收敛速度和寻优能力。针对制造业的生产配送路径优化,王楠、李世其、王峻峰[6]建立了适用于汽车总装线物料配送路径规划的混合时间窗模型,提出了改进遗传算法,朱永国、李俊杰、刘春锋[7]等针对飞机装配过程中装配工位物料需求时间模糊化现象,建立了基于正态模糊时间窗约束的配送路径规划模型,采用遗传算法进行了求解,夏扬坤、符卓、谢九勇[8]将多自动导引车物料配送路径规划问题归结为一种带软时间窗的需求依订单拆分车辆路径问题,设计了一种自适应禁忌搜索算法,李思国、郭宇、王益聪等[9]针对离散制造车间环境复杂以工作中心为物料配送基础结合物料配送时间窗要求,以最小物料配送成本为优化目标,建立了车间实时环境下的物料配送模型,采用改进遗传算法对模型进行求解。Emde S,Boysen N[10]通过设计配送小火车的运行路线和到达站点时间,实现准时化配送,并设计优化模型计算精确解。
综上所述,近年来针对制造车间路径规划的研究主要是结合工位需求的配送路径建模,并使用智能算法求解,但大多数研究并未考虑车间内实际布局和道路规划。本文以农机混流车间配送路径规划为研究对象,结合混流车间布局的复杂性,考虑线边空间和配送运载能力,以最小配送距离和线边库存为优化目标,建立物料配送和线边储存优化模型,设计改进蚁群算法求解最优配送路径,通过实例数据计算验证,确定最优配送 方案。
1 问题描述
农机混流装配车间路径规划是配送车辆从仓库出发,根据工位物料需求,确定配送小车需要配送的物料和需要服务的工位,通过合理规划配送路径和配送数量,在符合约束和确保生产的前提下,产生最少的配送成本和线边库存成本。
由于农业机械作业对象种类多,作业环境复杂,农机装备制造存在机型多,选配多的问题,在混流生产中体现出物料种类多,工位需求变动大等特点,因此大量线边库存和固定路径的周期性配送不能满足动态化的生产要求,需要根据工位物料需求变化,调整配送小车装载的物料型号和配送路径。同时生产车间路径规划受到车间布局和道路规划影响,导致配送小车在实际配送中存在不可行区域,加大了最优路径规划的难度。
2 优化模型
为解决配送路径规划困难,实现小批量多频次配送,减少线边库存,考虑各工位生产物料需求和配送小车的运载能力,以最小配送距离和线边库存为优化目标,建立优化模型。
2.1 相关假设
模型假设车间有n辆配送小车对m个工位进行配送,小车从仓库出发,根据某段时间的工位物料需求,配送若干工位后,空载返回仓库,在配送中满足以下假设条件:
1)本文所针对的物料主要是体积中等,型号种类复杂的装配件和自制件,每个工位仅装配一种物料。
2)在配送中一辆配送小车可以一次对多个工位进行服务,但一个工位一次只接受一辆小车服务。
3)物料体积、配送小车容量和线边储存空间已知且设定为标准料箱大小的整数倍。
4)仓库备货能力充足。
2.2 符号定义
i= {i | i=1,2,…,n}:配送小车集合,车间内配送小车数量为n;
j={j,k | j,k=1,2,…,m}:工位集合,车间内工位数量为m;
djk:j工位到k工位距离;
Li:i小车的总配送距离;
Λj:j工位线边储存空间;
V:配送小车装载空间;
vj:j工位单位物料占用标准空间;
s:配送小车的运行速度;
Tload:配送小车服务工位时间;
qij:小车i对j工位一次配送的物料数量;
R:生产节拍;
cs:单位物料线边库存成本;
cd:单位距离配送成本;

2.3 数学模型
目标函数:

相关约束:
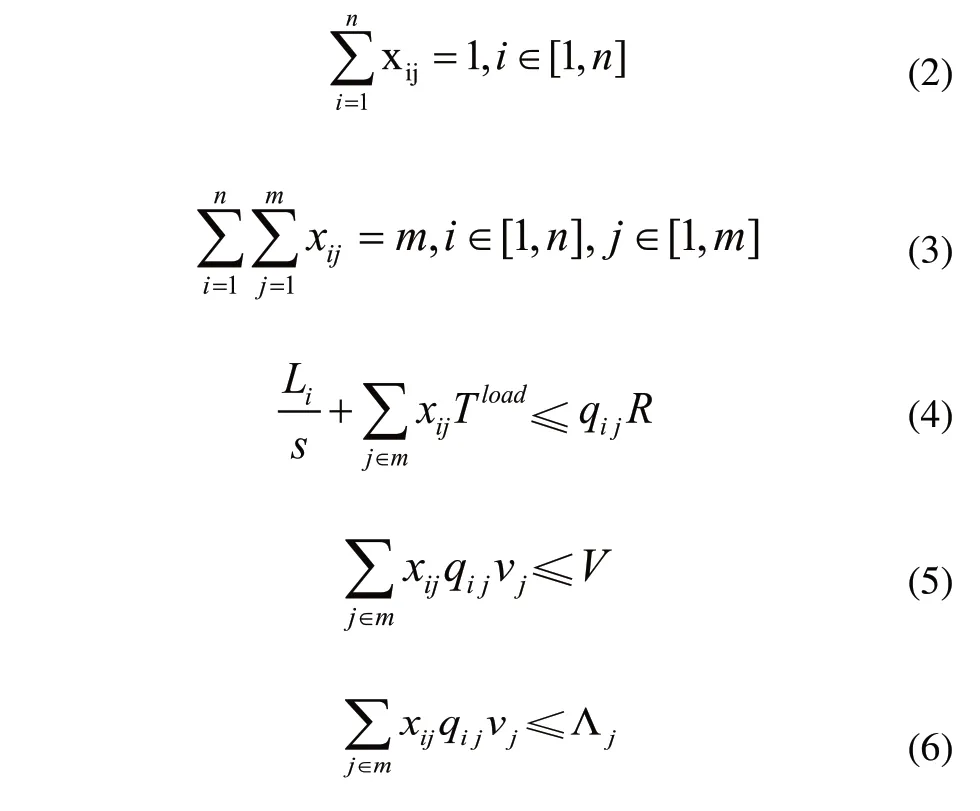
式(1)为目标函数,包括线边库存成本和配送成本,式(2)表示一个工位只接受一台配送车辆服务,式(3)为所有需求工位都安排了配送车辆,式(4)为配送时间要求,表示物料需求有一定的时间窗,式(5)和式(6)表示配送物料不能超过配送运载能力和线边库存空间。
3 蚁群算法设计
由于小车装载和路径调度问题属于NP-Hard问题,因此在大规模问题中,精确算法很难快速获得理想的解,蚁群算法在路径规划等领域具有较强的全局搜索能力,因此本文设计了结合车间物流配送特点的改进蚁群优化算法。
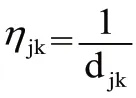
2)设置地形图矩阵,将车间布局和道路规划通过01矩阵表现,矩阵中1表示为障碍物,是蚂蚁不可行区域,0为道路和空地。设置蚂蚁路径起始点为仓库,将各工位位置转换成坐标形式,放入地形图矩阵中,通过地形图计算蚂蚁在两工位间的实际路径距离和节点之间的可见度。
3)存储每一代每只蚂蚁的爬行路径和爬行路线长度,蚂蚁已经访问过的工位设置为工位集合禁忌表,并由此获得蚂蚁下一步可以访问的工位集合allowdn,
4)改进蚁群算法的路径选择概率,结合配送小车的配送能力约束和各车间工位的物料需求情况改变蚂蚁的选择概率,在此加入式(7)和式(8),使蚂蚁在选择时,具有提高装载率的偏向,然后通过式(9)计算蚂蚁i的转移概率,并使用轮盘赌法选择下一个访问的 工位。

5)根据之前蚂蚁的路径选择,进行局部信息素更新,直到配送过程中所有蚂蚁都生成网络路径。

6)根据蚂蚁的路径选择信息,进行网络全局信息素更新后,计算物流配送过程中蚂蚁经过的最短网络路径总长度。
7)当迭代循环次数NK>NKmax,则停止迭代循环,输出蚂蚁走过的路径和路径总长度,此时最后一次迭代结果即为最优配送路径。
4 实例分析
4.1 实例数据
实例选取某拖拉机总装车间现场生产数据,实验中的配送为车间内生产配送,主要是指从总装车间仓库配送到各装配工位的过程,该车间布局主要由总装线、驾驶室组合区、前箱组合区,后箱组合区、前后箱组合线等装配线组成,根据装配线的工艺装配顺序要求、物料需求时间窗和物料管理划分,将有工艺要求和距离相近的工位整合,最终设定为7个工位段,且4个组合区的物料必须先于总装区到达。在计算中设置配送车辆容量V=600,生产节拍R=2.5分钟,Tload=3分钟,配送小车行驶速度为s=1m/s,单位配送距离成本cd=1,线边库存成本cs=1,工位段需求情况如表1所示。

表1 工位段物料需求情况
4.2 实验结果
在实际生产中,由于受到车间内布局和道路情况影响,导致实际配送距离大于坐标直接计算结果,车间各工位之间的实际配送距离不能用坐标直接计算,本文在蚁群算法中设置车间栅格地形图,设定配送小车可以运行的路线,通过计算确定各工位间的最短配送距离,代替传统蚁群算法中城市位置用横纵坐标计算的方法。地形图中黑色部分代表配送小车不可行驶区域,图形中设定每单位方块的边长为10米,计算仓库到达后箱组合区工位的最短配送车间栅格地形路线如图1所示,计算过程如图2所示,最短路径距离为250米,同理可以计算获得各工位之间配送距离如表2所示。设置算法参数α=1,β=5,γ=0.2,蚁群规模m=10,最大迭代次数K=100。使用Matlab7.0进行实例计算。

图1 仓库到后箱组合区配送路径

图2 仓库到后箱组合区配送路径计算

表2 仓库和各工位配送距离表
当蚁群算法不考虑装载能力和工位需求时,1台配送小车对7个工位段进行配送,得到最短路径的配送方案是:1-3-5-6-7-4-2-1,此时配送距离为1210米,小车配送时间和装卸货时间总和为2290秒,但此时配送不能满足工艺顺序和物料数量需求。
因此改进后的蚁群算法在蚂蚁进行轮盘赌选择下一个将到达的工位时,需要对比工位的物料需求和蚂蚁剩余的运载能力,若余下工位全部不能满足装载要求,则蚂蚁将返回仓库,重新装载后出发配送。
改进后蚁群算法计算最优路径为1-5-7-3-1-2-6-4-1,此时满足约束条件且成本最低的配送方案为2台配送小车,配送路径为:
车辆一配送路径是:1-5-7-3-1,即仓库-后箱组合-发动机组合-总装A区-仓库,每次迭代蚂蚁配送最短距离和平均距离计算过程如图3所示,最终最短配送距离830米,配送时间和工位服务时间为1370秒,装载率为83%。
车辆二配送路径是:1-2-6-4-1,即仓库-驾驶室组合-前箱组合-总装B区-仓库,最短配送距离为590米,配送时间和工位服务时间总和为1130秒,装载率为83%。
考虑配送宽放时间后,可以设置为配送间隔期25分钟,每种物料单次配送量10个,总配送距离为1420米,此时总成本为1820,实现了配送路径优化和线边库存量减少。
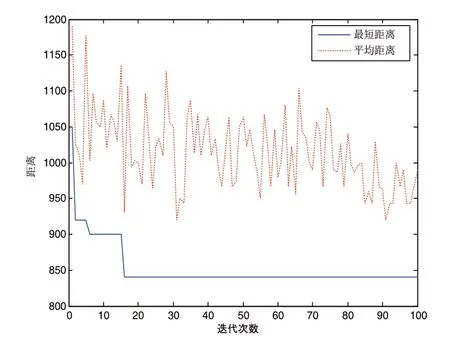
图3 车辆一配送距离迭代变化图
5 结束语
针对农机装备混流车间线边库存量大,配送路径难规划的问题,研究了优化目标为配送距离和线边库存量的配送模型,设计了结合配送能力的改进蚁群算法,以某拖拉机总装车间配送数据实例分析,确定了最优配送路径和配送期量,为农机装备混流生产配送路径优化提供理论依据。

