灵巧手指面压力与驱动电机电流关系的建模
化徐勇,谢 峰,陈 亮
(1.安徽大学 电气工程与自动化学院,合肥 230601;2.安徽科学技术研究院,合肥 230001)
0 引言
灵巧手作为工业机器人和服务机器人中常见的末端机构,其高度的灵活性和拓展性相较于其他末段工具而言有着很大的优势,特别是在服务机器人技术领域,灵巧手是十分重要的一环,所以近年来灵巧手的相关技术也成为了研究的热点[1,2]。同时,对于灵巧手指面压力的控制一直是该领域的研究难点。灵巧手在抓取过程中,不仅需要完成对不同尺寸物体的抓取操作,还要避免在抓取过程中因指面压力过大导致柔软或易碎物体发生损坏或因指面压力过小导致物体脱落,所以需要对指面压力进行实时的预测和控制。
德国宇航局率先在其所研发的DLR-Ⅰ和DLR-Ⅱ多指灵巧手加入触觉传感器,从而实现对指面压力的检测;哈尔滨工业大学与德国宇航中心联合研制的HIT/DLR-Ⅱ手具有了很高的集成度和丰富的感知功能[3,4]。鉴于触觉传感器的布置增加了灵巧手的成本和制造难度,所以本文拟采用力传感器来检测出灵巧手的指面压力,并建立驱动电机电流与指面压力间的关系,达到通过检测灵巧手驱动电机电流来对指面压力进行预测和控制的目的。
在测量力信号与电流信号过程中,受传感器信号调理电路的热噪声、周围环境噪声与电磁噪声的影响,测得的信号会出现较大的信号漂移,如何对信号进行降噪处理是准确建模的关键。Donoho等人对信号提出了基于小波分析的阈值去噪理论[5],在噪声的滤除上取得了很好的效果,但在选取阈值的过程中,会受到信号和噪声的统计特性的限制;Deasy于2000年首先设计出了二维的Savitzky-Golay算子,在二维信号的噪声去除上取得了重要进展[5]。
本文拟通过力传感器与电流传感器,同步测得指面压力与驱动电机电流的原始信号,然后运用Savitzky-Golay滤波算法对原始信号中的噪声进行滤波处理,接着采用最小二乘法曲线拟合对指面压力与驱动电机电流的关系进行建模,所建立的数学模型可以反映指面压力随驱动电机电流变化的趋势,并且通过两者的数学关系式可以依据测得的驱动电机电流值计算出实时的指面压力值,从而更好地预测和控制灵巧手的指面压力。
1 具有力传感器与电流传感器的灵巧手实验装置
本实验的研究对象为三关节五指仿生灵巧手,该装置的结构三维图如图1所示,该装置采用拟人化的设计方法,以人手近指节、中指节和元指节1:1:0.6的比例关系为参考,从而设计出灵巧手手指各指节基本尺寸近似等同于真人手指尺寸。同时,该装置采取连杆结构加指节推杆的传动方式,该传动方式具有传递性能稳定,各指关节的转动角度范围可控性好等优点,从而使灵巧手在抓取物体时更加稳定。

图1 灵巧手的结构三维图
本实验通过在灵巧手远指节末端贴附力传感器从而实现手指末端指面压力F的实时采集,灵巧手单指结构示意图如图2所示,灵巧手的驱动电机通过舵盘带动腱杆连接至近指节E上的O点,腱杆带动E绕近指关节S旋转,中指关节N也随E沿曲线移动,同时带动曲连杆PQ使得中指节D绕中指关节N旋转,D绕N点旋转的同时带动曲连杆AB使得远指节C绕远指关节M旋转,这一传动过程即可完成手指弯曲或伸直动作,末端的力传感单元在手指动作时可采集指端的力值变化信息并传输至信号采集模块,其中力传感器型号为DYHW-110,测量量程0~30N,输出灵敏度为K1=0.5~10mV/V,该传感器采用金属箔式应变技术,适用于各种小空间的测力[6]。

图2 灵巧手单指结构示意图
对于灵巧手控制系统中驱动电机的电流检测,本实验采用WHB06LSP5S2H型号高精度霍尔电流传感器,该电流传感器可测量直流电流,测量量程为0~6A,传感器输出端电压Vout为0~5V电压输出,该输出端的实时输出值与被测电流I成正比例关系,满足Vout=0.83.I,即传感器灵敏度为K2=830mV/A。测量时电机电源线穿过霍尔传感器中间的穿孔,电机工作时,被测电流I通过霍尔元件并在元件两端产生霍尔电势VH,其大小正比于被测电流I[7],VH经运算放大器及调理电路后,最终得到输出电压Vout,其原理如图3所示。
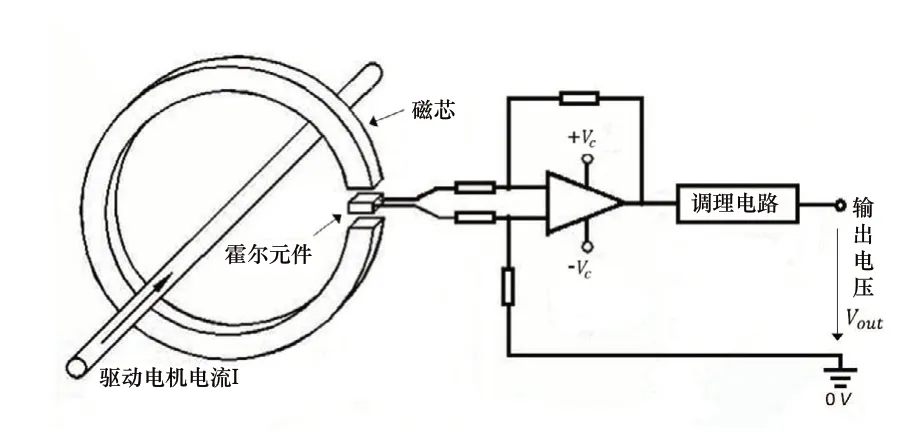
图3 电流检测模块原理图
2 灵巧手指面力信号与电流信号的采集及建模
2.1 信号采集实验系统的设计
灵巧手装置在添加力传感器和电流传感器后,需要对力信号与电流信号进行采集和处理,所搭建的实验系统工作流程如图4所示。

图4 实验系统工作流程
该系统由指面压力检测模块、驱动电机电流检测模块、灵巧手装置、传感器驱动电源、上位机、力传感器应变适调器和动态信号测试分析仪组成。其中,应变适调器和动态信号测试分析仪由东华测试公司生产,其型号为DH3810N-1和DH5922N,实验系统的配置如图5 所示。

图5 实验配置
为了对指面压力F与驱动电机电流I的关系进行建模,通过上位机对灵巧手控制系统发出抓取指令,使其对物体进行抓取动作。在此用350g钢块作为被抓取对象,在抓取的过程中力传感器与电流传感器所测量的指面压力F与电机电流I通过动态信号测试系统进行采集,设置动态信号测试系统的采样频率为2kHz,采样时间为7s,图6为动态信号测试系统所采集到的力传感器与电流传感器的原始信号。其中由于本实验选用的霍尔电流传感器配有特制的调理电路,该调理电路主要针对小电流及微弱电流情况下对信号起放大作用,所以输出得到的波形是周期为100ms脉冲式信号,如图6(b)所示,波形中,脉冲幅值处为该信号实时幅值。
2.2 基于Savitzky-Golay滤波算法的信号处理
Savitzky-Golay算法最初由Savitzky和Golay于1964年提出,发表于Analytical Chemistry杂志,之后被广泛地运用于数据流平滑除噪,是一种在时域内基于局域多项式最小二乘法拟合的滤波方法,与传统算法相比,Savitzky-Golay滤波算法具有更稳定,误差更小的平滑去噪效果。
其原理是基于最小二乘法多项式拟合算法,通过取点xi附近固定个数的点拟合一个多项式,多项式在xi的值,就给出了它的光滑数值gi(gi∈G)。用nl表示xi左边点的个数,用nr表示xi右边点的个数,pi(x)表示相对于点xi的一个M次多项式,用它在最小二乘意义下拟合这nl+nr+1个点。因此:


图6 系统所采集
对于力传感器所采集的力信号,如图6(a)所示,通过波形可以得知,在0~2.3s时间范围内,灵巧手指端未接触被抓取物体,力值为0N;在2.3s时刻后指面压力呈上升趋势,并在6.3s时刻处达到最大值3.249N。但采集的过程中受传感器信号调理电路的热噪声,周围环境噪声与电磁噪声的干扰,如图7所示,从4.12s~4.64s力信号放大图中可以明显看出所采集的力信号呈局部锯齿和尖刺状,说明测得的信号存在大量干扰和噪声,对接下来力信号与电流信号的标定存在一定影响,所以本实验中的下一步工作将对所采集的力信号进行Savitzky-Golay滤波算法处理。

图7 4.12s~4.64s力信号放大图
假设横坐标xi具有xi+1-xi≡Δx的均匀间距,设实测数据为yi。为了使用pi(x)拟合测试数据,必须定义系数bk,使得下式达到最优。

在MATLAB中运行Savitzky-Golay滤波算法对所测得的力信号进行降噪处理[8~10],处理结果如图8所示。

图8 Savitzky-Golay滤波处理前后的力信号对比图
由图8可以看出,对所测得的原始力信号施加Savitzky-Golay滤波算法后信号波形形状得到明显改观。对比图8(a)和图8(b),原始信号波形中的锯齿与尖刺基本被滤除,对3.9s~4.8s时间段的波形进行观察,可以得知滤波效果十分明显,且滤波后的信号仍保留原始信号中的主要特征,为接下来的实验数据点选取和指面压力与驱动电机电流关系的建模提供了更加可靠的数据支撑。
2.3 手指传递系统的动力学模型分析
通常,灵巧手单指传递系统可看成一个整体,其包括驱动电机惯量、传递系统惯量、抓取负载惯量等。整个传递系统主要受到不断变化的末端接触压力、传动部件反作用力、关节转轴摩擦力等作用。其传递方程为:

其中:T代表驱动电机转矩,JS代表传动部件的总惯量,ωs代表驱动电机角速度,Tfs代表摩擦力矩,Th代表末端接触力矩。
摩擦力矩Tfs主要包括两部分:传动杆摩擦力矩和关节转轴摩擦力矩,即:

其中fp为传动杆摩擦阻尼系数,Vp传动进给速度,fj为指关节转动阻尼系数,ωj为指关节转动角速度。
指面压力与末端接触力矩之间的关系可以表示为:Th=rFh,r为远指节转动半径,Fh为指面压力,则式(3)可表示为:同样,驱动电机输出的力矩与驱动电机电流存在一定的关系,即电机转矩T为:
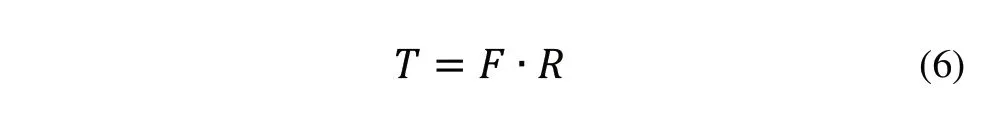

其中F为力,R为作用半径,同时:F=P/V,其中P为功率,V为速度;且V=2πRN,其中,N为每分钟转速;可得T=P/2πN ;所以:
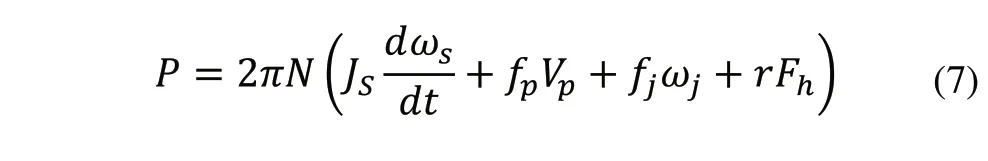
理论上认为系统中电源电压是不变的,所以功率与电流之间成正比。则:

式(8)即为灵巧手系统单指传递模块中指面压力与驱动电机电流之间的关系模型,此模型的建立,为进一步研究所采集的力信号与电流信号之间的关系奠定了理论基础。
2.4 指面压力与驱动电机电流关系的建模
为了得到灵巧手指面压力F与驱动电机电流I的关系,接下来对测得的力信号与电流信号进行时域同步对应,以电流信号脉冲周期为间隔,选取同一时刻两者的瞬时值作为一组实验数据点。由于在2.3s时刻前灵巧手手指末端未接触被抓取物体,力值为0且电机电流为空载电流,所以选择2.2s~6.4s时间段内力值与电流值的变化信息,并得到36组驱动电机电流I与所对应的指面压力F的实验数据点(Ii,Fi)(i=1,2,…,36)如图9、图10和图11所示。由图可知当驱动电机电流小于50mA时,抓取力为0,说明灵巧手手指末端未接触被抓取物体;随着驱动电机电流的逐渐增大,力值便随着电流的增大而增大,说明灵巧手不断抓紧被抓取物体。

图9 实验数据点及1阶拟合曲线

图10 实验数据点及2阶拟合曲线

图11 实验数据点及3阶拟合曲线
为得到灵巧手指面压力F与驱动电机电流I的关系,采用最小二乘法对36组实验数据点进行多项式拟合[11~13],拟合曲线可表示为:

其中: 为拟合表达式所计算出的预测值,m为多项式阶数,ai(i=0,1,…,m)为多项式待定系数,则力传感器测的指面压力实际值Fi和预测值 之间的偏差平方和可表示为:
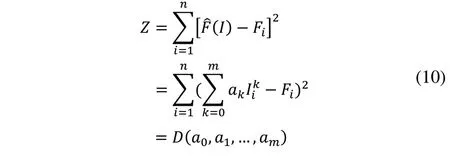
其中:n为实验数据点数,n=36;Ii为第i个驱动电机电流值。鉴于Ii和Fi均为已知数值,所以偏差平方和Z为多项式待定系数ak(k=0,1,…,m)的函数。曲线拟合的直接目的是让偏差平方和Z最小,这样便能使所拟合的曲线能准确表达指面压力F与驱动电机电流I之间的关系,即函数D(ak)(k=0,1,…,m)出现最小值,由极值条件可得知其最小值存在的必要条件是D(ak)(k=0,1,…,m)对ak的偏导为0,即:
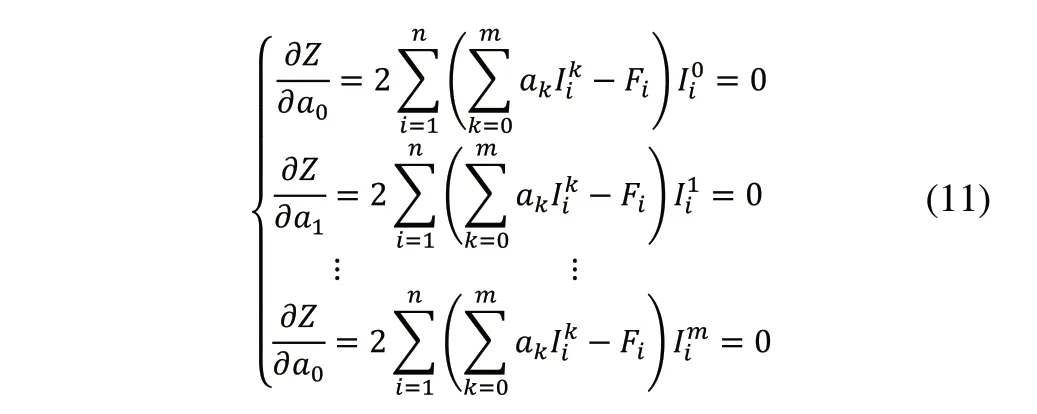
即求:

式(12)可写成如下的矩阵形式:


其中: 通过式(13)求解可得到线性方程组的唯一解ak(k=0,1,…,m),进而确定式(9)所示的拟合函数。为了选取合适的拟合曲线反应指面压力与驱动电机电流之间的关系,分别采用1阶、2阶和3阶多项式进行拟合,其表达式分别为:

式中:1(I)、2(I)和3(I)分别表示1阶、2阶和3阶多项式拟合对应的指面压力,其对应的拟合曲线分别如图9、图10和图11所示。由图可知,在拟合精度方面,3阶多项式比1阶和2阶多项式要更好。
现采用相关系数R2来定量衡量回归模型的精度,R2可表示为:
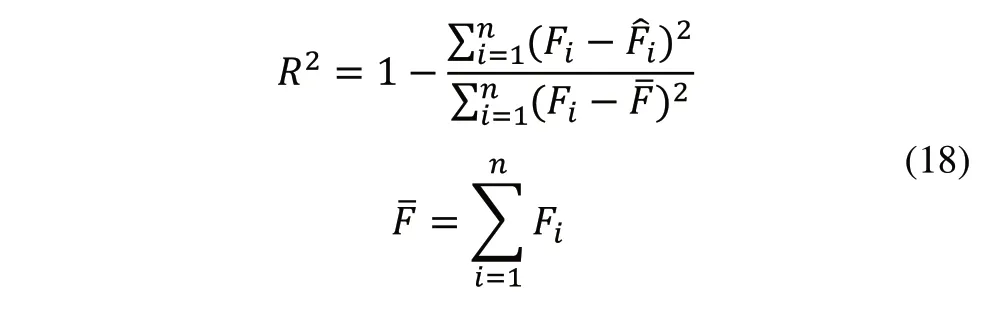
若要拟合曲线的精度更高,则需让R2的值更接近于1,联合上式可分别求得反映1阶、2阶和3阶多项式拟合精度的指标R2的值分别为0.999953、0.999971和0.999985,可以看出3阶多项式的评价指标R2值最大,说明3阶多项式拟合曲线精度最高,所以选择式(17)作为反映灵巧手指面压力F与驱动电机电流I之间关系的表 达式。
图12为指面压力与驱动电机电流关系的残差分布图,其中残差ΔF分布的范围为[-0.424,0.492]N,ΔF较小且均分布在0线两侧附近,说明所得出的拟合曲线能很好地反映指面压力与驱动电机电流之间的关系。
通过以上分析最终得到指面压力F与驱动电机电流I的关系为:

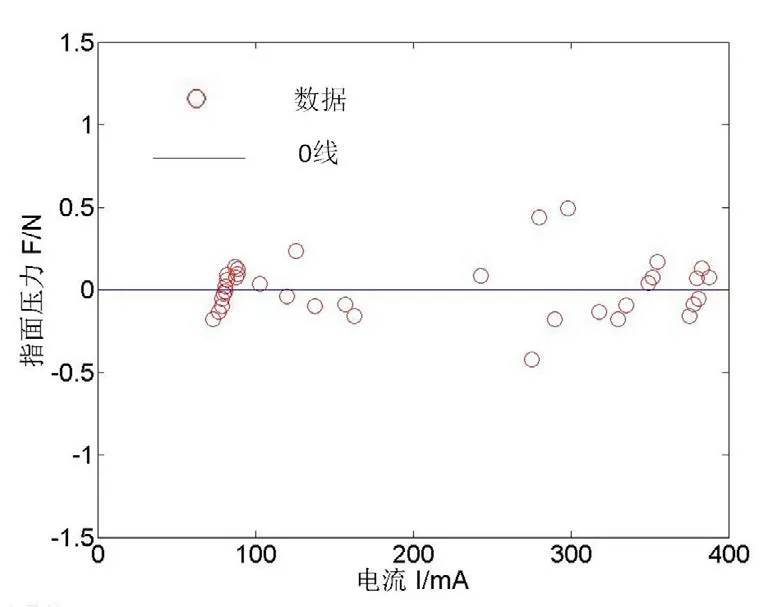
图12 反映指面压力与驱动电机电流关系的残差分布
式中:I的范围为0~400mA,指面压力F单位为N,如图13所示,图中指面压力F-驱动电机电流I之间的变化曲线对应式(19)中的关系式。同时,从图13中的曲线可以看出,驱动电机电流在56.12mA~137.8mA范围内曲线较为倾斜,说明此时指面压力随驱动电机电流变化较快,对应的阶段为灵巧手手指指面刚开始接触物件但未抓紧;驱动电机电流在137.8mA~268.8mA范围内曲线较为平缓,对应的阶段为灵巧手克服装置内的机构间隙,传动机构逐渐消除传动机构的间隙和弹性变形,电流负载不断上升,但手指末端指面压力的变化则不明显;驱动电机电流在268.8mA~397.5mA范围内曲线不断倾斜,对应的阶段为传动机构已开始夹紧工件,驱动电机输出转矩不断增大,指面压力也随之急剧上升,最终电机堵转,指面压力与驱动电机电流均达到最大值。所以,结合指面压力和驱动电机电流的关系式与关系曲线即可对指面压力进行预测和控制。

图13 灵巧手指面压力与驱动电机电流的关系
3 结论
本文提出一种对灵巧手指面压力与驱动电机电流关系建模的思路,通过设计指面压力检测模块和驱动电机电流检测模块,实现对灵巧手装置指面压力信号和驱动电机电流信号的实时采集,并运用Savitzky-Golay滤波算法对所采集到的信号进行滤波优化处理,使得经优化后的信号能准确反映被测单元的变化特征。对优化后的力信号和电流信号运用最小二乘法曲线拟合进行建模,建模所得的3阶多项式可以很好地描述指面压力与电机电流之间的关系,用相关系数R2来衡量拟合曲线的精度,并得到R2=0.999985,且计算所得的指面压力残差ΔF均分布在0线两侧附近,进一步说明所建立的拟合曲线能准确反映指面压力与电流之间的关系,从而能够实现对指面压力更好的预测和控制。所提出通过检测驱动电机电流来预测灵巧手指面压力的方法和基于Savitzky-Golay滤波算法的信号滤波方法为灵巧手控制提供一种新的思路。

