适用于连续拐角高速加工的中点约束算法
王 勇,张立强,郭景浩
(上海工程技术大学 机械与汽车工程学院,上海 201620)
0 引言
在复杂曲面的高速加工中,通常根据允许误差、机床动力学等约束条件使用CAD/CAM把复杂曲面离散成一系列连续微小线段。但这一过程中并未充分考虑连续小线段间的平滑过渡问题,导致系统的频繁启停,对机床造成很大的冲击,难以在保证加工质量和加工效率[1]。近年来在一些科研学者不断对早期的直线插补和圆弧插补做出改进[2~4]。同样发展迅速的还有各种样条曲线插补方法,即用高阶样条曲线进行插补以平滑加工路径中尖锐拐角,使得机床可以在加工路径的拐角处实现连续不间断进给运动,常见的样条曲线有:PH,Bezier和NURBS曲线等[5~7]。此外还有学者从运动学角度探究全局拐角光顺,文献[8]和文献[9]提出了基于跃度约束的适用于高速加工的拐角光顺方法,文献[10]更进一步提出了基于跳度约束的运动学平滑算法。但在上述研究中,对于加工过程中的局部相邻拐角轮廓重叠现象研究较少。而在连续小线段实际加工过程中,这种特殊情况往往会出现。传统的点对点直接插补方式虽然可以避免此种现象,但是进给运动必须在路径拐角处减速至停止,否则,驱动器的加速度值或跃度值将有可能超出系统限制,导致加工零件表面的光滑度遭到破坏[11],形成具有明显进给标记的粗糙加工表面,还导致加工时间延长。文献[9]采用了参数约束的方式来限制进给速度,但加速度曲线还存在严重的突变点和不可导点,在拐角轮廓的中点加速度值会产生突变造成进给运动的惯性振动,会在工件表面形成明显的进给标记,影响加工质量。
根据文献[12]跳度约束加速曲线已被证实在减少机床振动和提高加工质量方面存在显著优越性。因此本文采用文献[10]所提运动学平滑算法实现拐角转接,并在其基础上提出中点约束法,在出现拐角轮廓重叠的情况时,设定两拐角间直线段的中点为约束点,限制过渡段长度,避免拐角轮廓重叠。同时实现进给运动在相邻拐角处的速度和加速度平滑转接。最后对所提算法进行实验分析,通过对比传统的点对点插补算法验证本文算法的有效性。
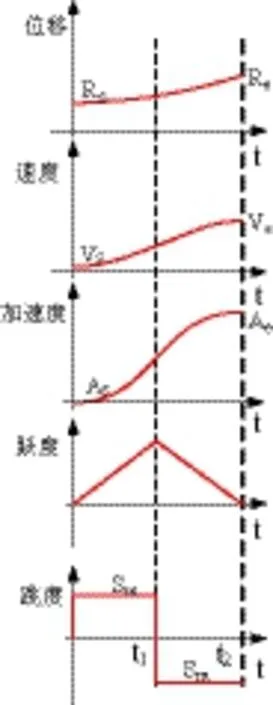
图1 跳度约束加速度原理
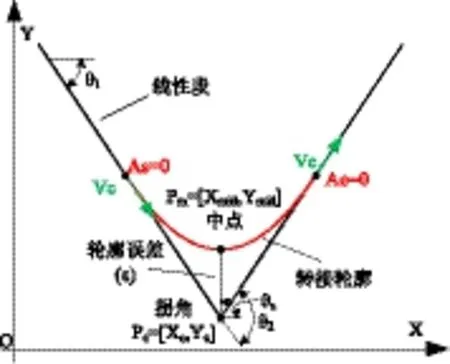
图2 拐角路径
1 相邻拐角中点约束算法
1.1 基于跳度约束的运动学平滑算法原理
跳度约束加速度的原理如图1所示,通过跳度限制加速度曲线生成平滑的速度和加速度转接轮廓,其限制进给轴从初始速度和加速度平滑过渡到最终速度和加速度,在已知位移Rs、速度Vs和加速度As、跳度极限Sm和加速度极限Am的情况下,可以通过对跳度曲线s(t)积分来获得跃度j(t)、加速度a(t)、速度v(t)和位移r(t)曲线的计算公式,如式(1)所示。
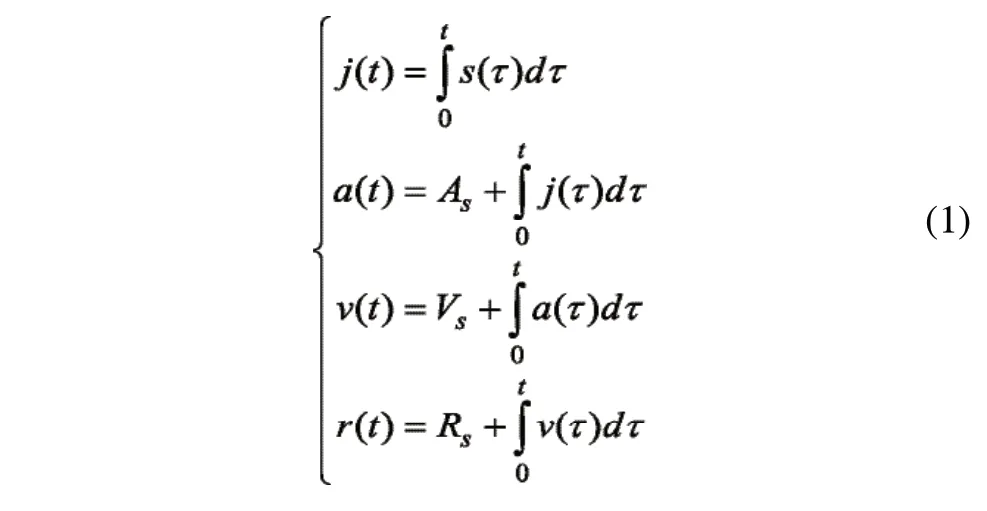
平滑算法原理为:针对连续短线段刀具路径中的拐角,通过跳度约束加速度曲线,同时施加速度、加速度和轮廓误差等边界条件,在满足驱动器运动学限制条件下推导最佳转接速度。如图2所示刀具加工拐角路径中,两个线段方向夹角分别是q1和q1+q2,拐角点PC=[XC,YC]。刀具在拐角附近以初始速度VC和初始加速度AS进入拐角,S为跳度值,T1为进给轴的转接持续时间,Vs为转接运动开始处的速度,Ve为转接运动结束处的速度,设定最大轮廓误差为ε。根据转接运动轮廓的几何形状和总位移来计算。可推导出过渡段长度Rc:
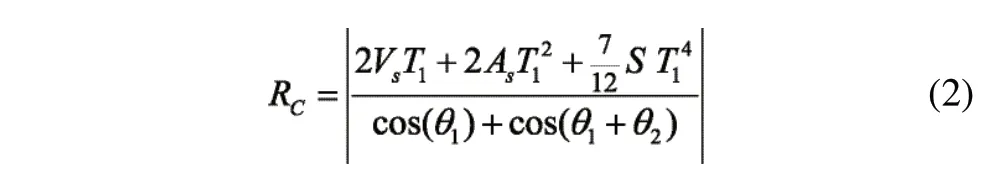
通过确定限制轴,从而推导出该轴的最佳转接速度。假设X轴是限制轴,那么限制轴的加速度、速度和最大轮廓误差约束为:
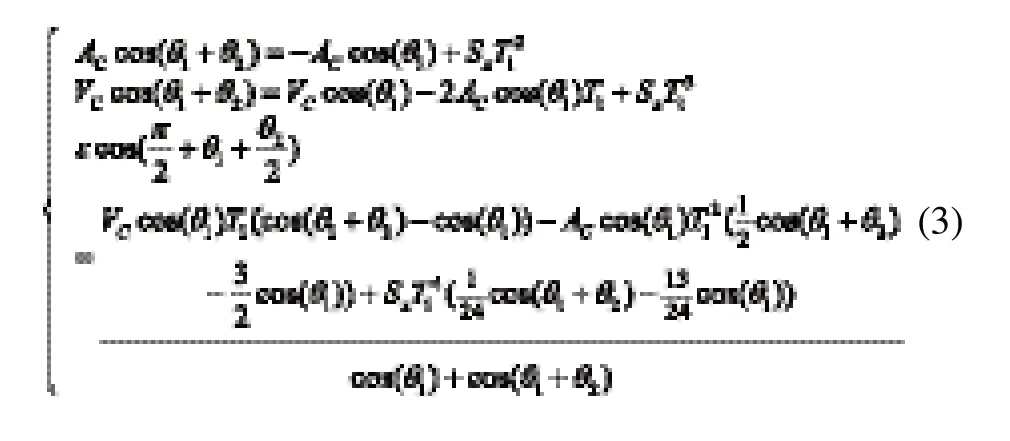
文献[10]中给出了上述式(2)和式(3)的详细推导 过程。
1.2 中点约束法
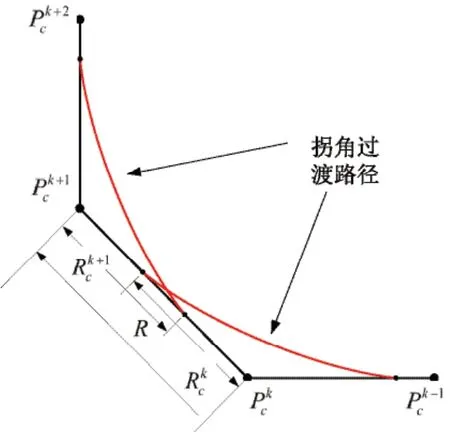
图3 相邻拐角轮廓重叠
尽管运动学平滑算法能够实现在连续短线段刀具路径加工时进给轴速度和加速度平滑转接。但未能考虑到相邻拐角间线段长度和拐角过渡段长度的关系,加工过程中可能存在拐角过渡轮廓重叠的现象,如图3所示。两个拐角轮廓间短线段的距离为:
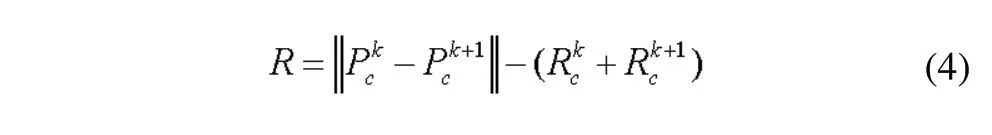
为便于计算设定:
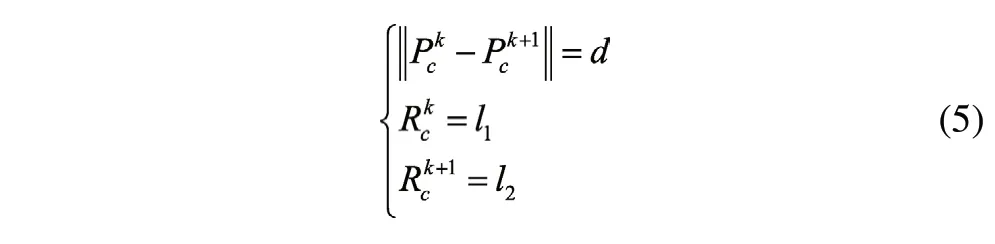
其中d为两拐角间直线段长度,l1为前一拐角过渡段长度,l2为后一拐角过渡段长度。
如果R>0,则说明k和k+1个拐角轮廓没有发生重叠,该短线段处前后两个拐角都是独立拐角,互不影响。如果R<0,则说明k和k+1个拐角轮廓相互重叠,说明该短线段处的前后两个拐角相互影响,一旦出现这种情况,进给运动必须在拐角处降低转接速度,否则重叠部分的进给运动就会超出驱动系统的限制,引起机床进给颤动。同时导致加速度轮廓也会存在跳动或不可导点,影响加工质量。
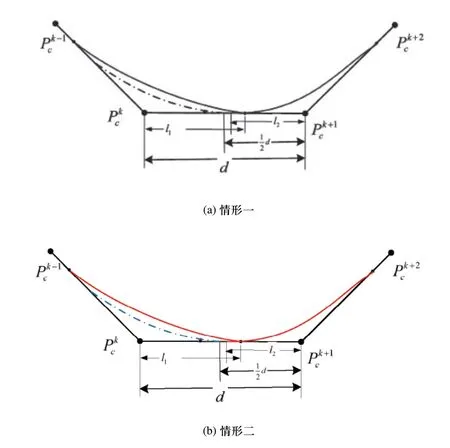
图4 拐角轮廓重叠情形
本节针对这一特殊加工现象提出中点约束法,当出现拐角轮廓相互重叠情况时,主要分为以下两种情形:
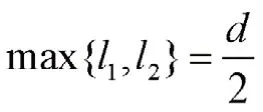
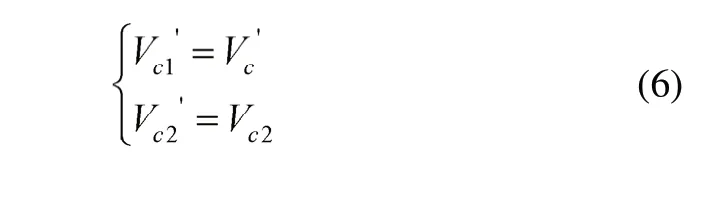
中点约束法即:选定段长中点作为过渡段的约束点,限制过渡段的段长,并将其作为已知参数,重新求解拐角转接速度。以X轴为例,对式(2)和式(3)做变换处理后如下所示:
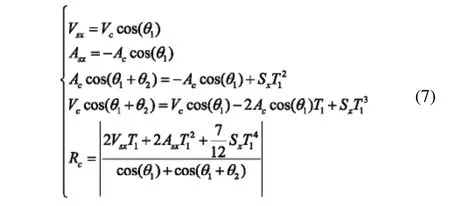
其中,Vsx、Asx分别为X轴的初始速度和加速度。在考虑驱动器运动性能的前提下,通过限制驱动器加速度或跳度极限,求解最大转接速度。假设限制轴以驱动器最大跳度极限进给,则Sx=Smax代入式(7)求得最佳转接速度为:

假设限制轴以驱动器最大加速度进给时,则令A=Amax可求得最大转接速度为:
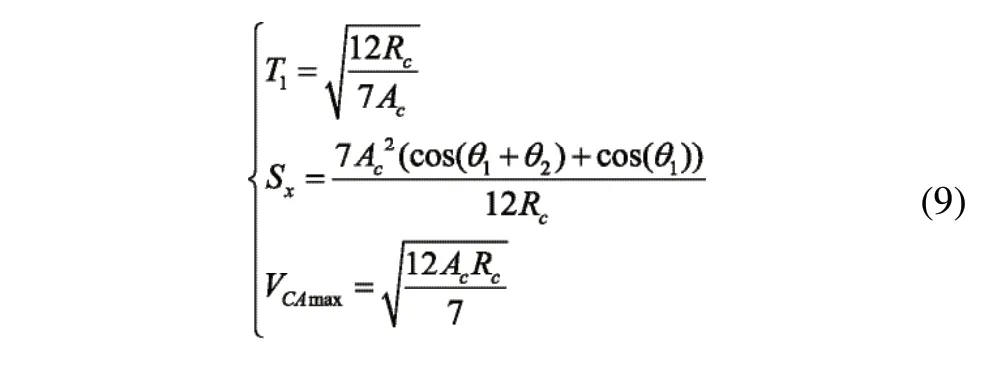
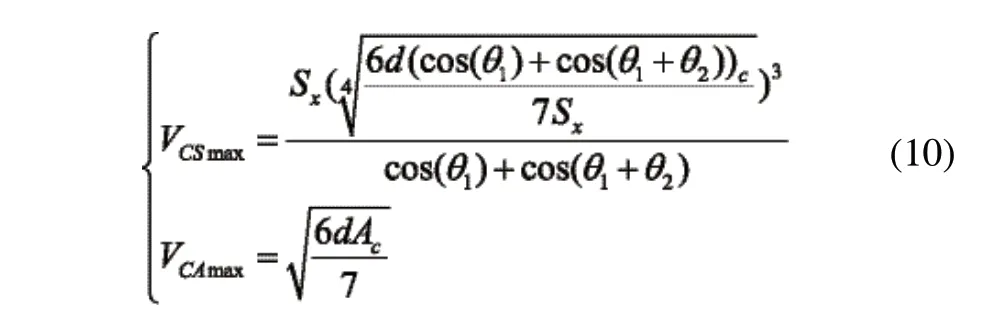
最佳转接速度为:
由此计算出新的转接速度V'c:
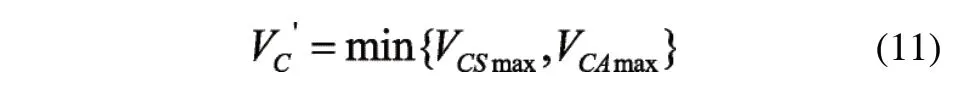
通过上述方法,可以避免相邻拐角出现轮廓重叠现象并获得拐角最佳转接速度,同时确保拐角过渡过程中速度和加速度平滑转接。
1.3 算法流程
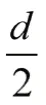
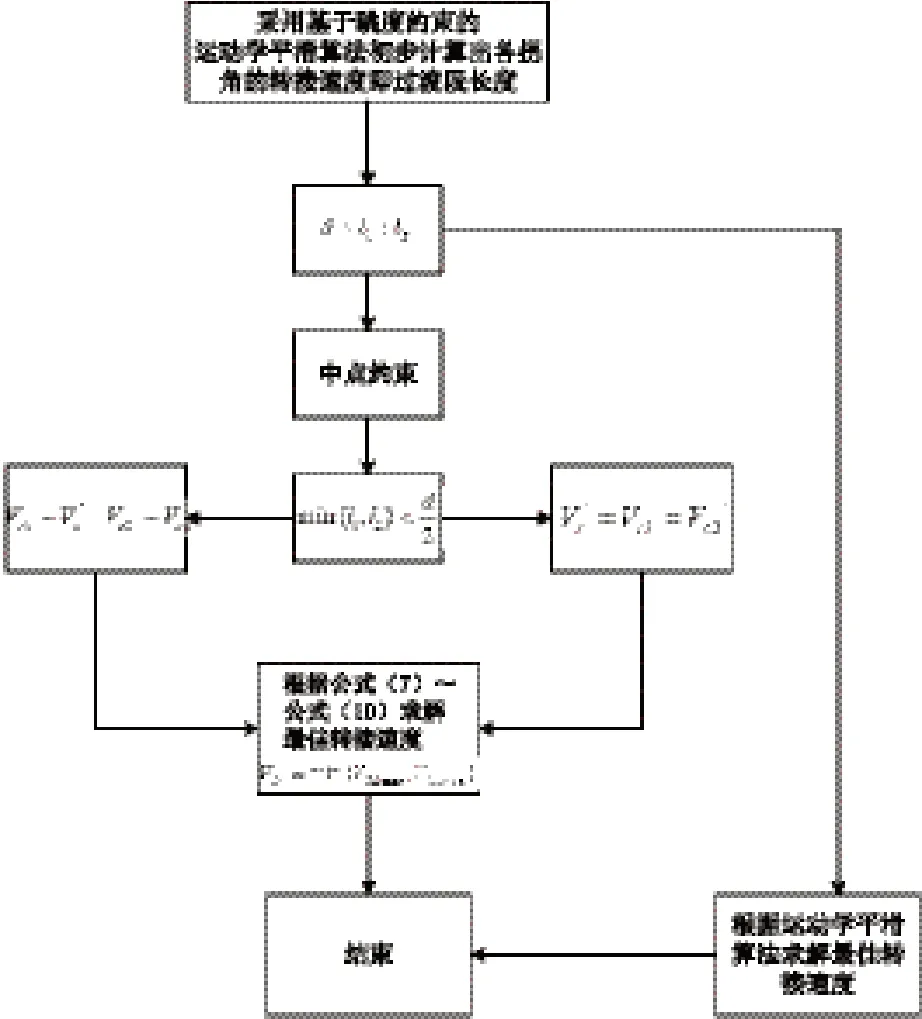
图5 算法流程图
2 仿真分析
为了验证所提算法的有效性,对连续短线段加工路径分别采用中点约束法和传统点对点直接插补算法进行对比分析。

图6 实验设备
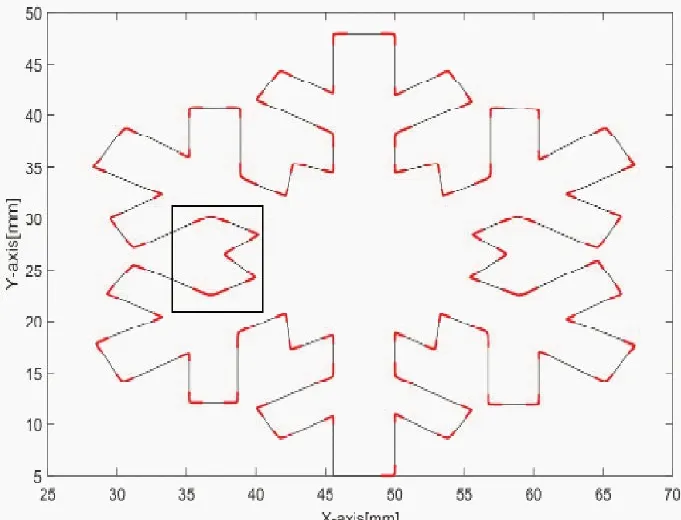
图7 加工路径
实验设备如图6所示,平面X-Y运动由两个线性电机驱动,保证良好的位置同步和路径跟踪,伺服放大器设置为转矩(电流)控制模式,线性编码器的反馈分辨率为0.8um,伺服系统的闭环采样时间为0.1ms,X和Y轴的位置反馈带宽为wn=25Hz。实验加工路径为如图7所示的“雪花”路径,总长度296.25cm,共有77个 拐角。
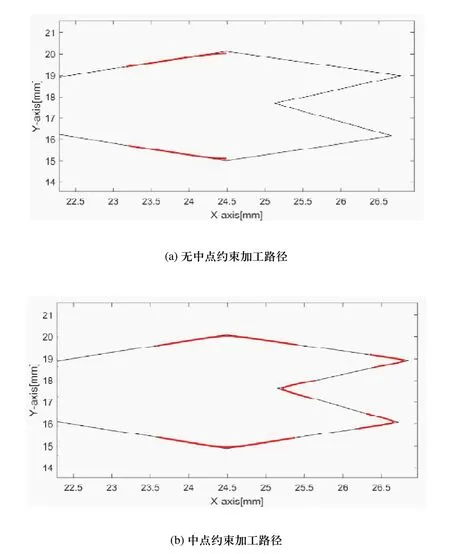
图8 局部路径示意图
图8(a)和图8(b)所示为图7中黑框所示的局部路径。在此段局部路径上相邻拐角间距较小,因此导致转接路径重叠,不仅无法完成当前拐角转接,还影响到后续拐角过渡,如图8(a)所示。图8(b)为采用了中点约束法避免拐角重叠现象的局部路径,在相邻拐角间完成平滑转接。
为体现该方法能够发挥驱动器的性能,将其与传统点对点直接差补算法进行对比。其中点对点插补算法要求刀具运动到每个拐角点前开始减速,直至拐角处完全停止,再进行转向进给,完全与G01代码所规定的路径同步;实验设定最大允许轮廓误差为0.1mm,利用伺服控制器对不同算法进行实时采样和命令。设置驱动器各轴的最大进给速度为100mm/s,最大加速度为1000cm/s2,最大跃度为1×105mm/s4,最大跳度为2×107mm/s4。图9所示为两种算法在加工路径上运动的速度曲线轮廓,可以看出点对点插补算法速度曲线存在较大的波动,且该算法需要在每一个拐角处完全停止,加速度跳动,对驱动器的负载较大。从图中还可以看出中点约束算法花费的时间为10.28s,点对点算法花费11.08s,加工效率提升了6.8%。同时本文所提算法的加速度曲线达到G1连续如图10所示。
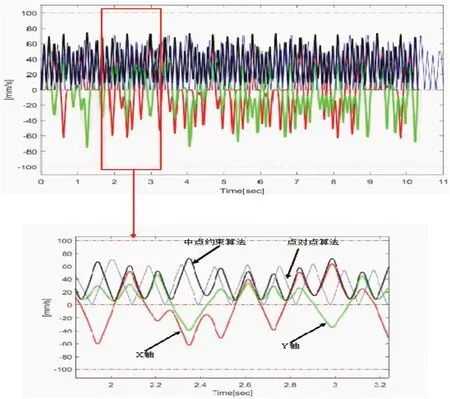
图9 中点约束算法和点对点插补算法速度曲线
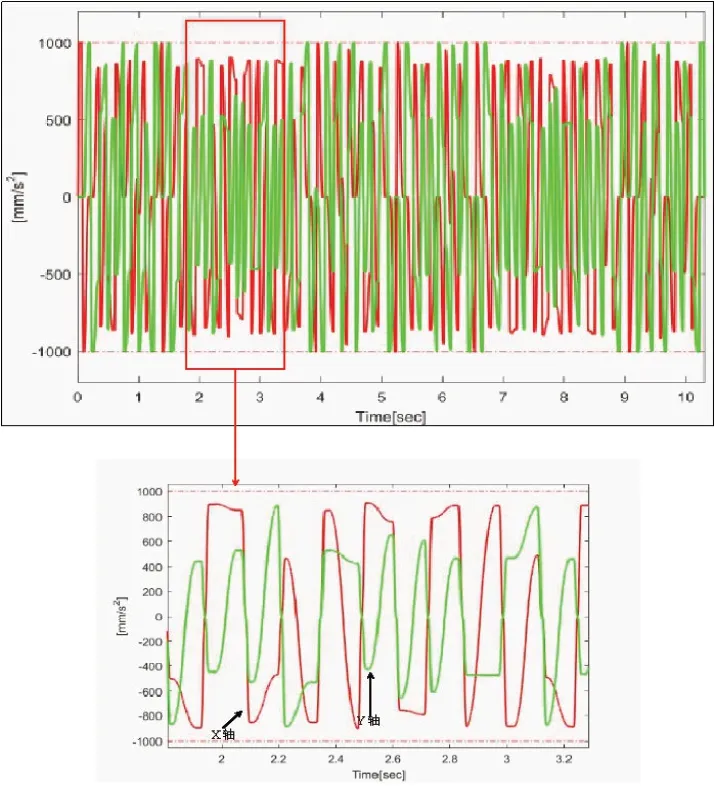
图10 中点约束算法加速度曲线
3 结束语
本文采用基于跳度来约束加速度曲线的方式,针对加工路径中的特殊情况即相邻拐角轮廓重叠提出中点约束法,限制过渡段长度从而防止拐角转接轮廓重叠,同时实现平滑的速度和加速度转接,加速度曲线达到G1连续。最后通过实验对比本文算法与传统点对点直接插补算法,发现中点约束算法的加工时间相比于点对点插补算法减少6.8%,加工效率得到提高。

