竞争市场环境下零售商团购营销的斯塔克尔伯格博弈分析*
□ 冉文学,杨礼凡,王 艳
(1.云南财经大学 物流学院,云南 昆明 650221;2.红河学院 商学院,云南 蒙自 661100)
1 引言
零售终端组织团购会是一种很常见的营销模式,比如电脑团购、汽车团购等。销售方设定一定的团购数量限制,并在零售价的基础上给予一定的团购优惠。当团购会的团购数量达到企业设定的限定以后,交易达成,消费者获得一定的实惠,企业也增加自己的出货量。
在许多行业中,中小企业为了生存很多时候都选择跟随战略。这样的例子很多,如现阶段中国品牌的汽车一般都是跟随外资品牌的汽车以获得生存空间。在以往同时考虑竞争与合作的团购研究中,团购的采购成员决策大多是同时进行的,如Chen和Roma[1]考虑竞争环境下零售商团购,发现这样的合作反而会伤害到买家。Tran等[2]则讨论了当技术进步后制造商可能希望其经销商在采用传统的公布价格的同时采用团购机制。Chen等[3]则探讨了当买方对产品的估价是透明的和已知的信息时,买方合作的最佳形式是与所有买方只组织一个“竞标圈”。Deng等[4]则提出了一个有限容量卖家优化团购网站价格和最大交易规模的分析模型。给出了最优策略和相应的交易参数。
正是因为企业的团购能够给采购方和供应方带来巨大的好处。目前,有关企业团购的研究主要侧重在采购方的角度,如何更好的进行采购合作和提升购买力方面,比如Chipty[5]认为大企业与供应商的讨价还价能力大于小企业,持同样观点的还有Dana[6]以及Marvel和Yang[7]等。Chen等[8]探讨了不同团购机制下的采购企业的投标策略。OV Horne等[9]则研究了团购模式对小企业采购的影响。Weng[10]则采用内容分析法和解释理论和权变理论来分析了零售商单个购买和团购的影响。刘斌等[11]则探讨了应急采购的情形下零售商的团购决策。王甜源等[12]则重点讨论了两个零售商在既竞争又合作的条件下采购序贯博弈定价策略研究。综上所述,前人的研究侧重于研究采购方在团购中如何合作,以及相关的利益分配问题。用博弈论的方法研究供应方的利润分配的研究目前较少,有待进一步研究。
本文与以往研究的主要区别在于,以往的研究主要侧重于团购采购以及团购成员间的合作与利润分配。其主要是站在买方的角度探讨团购带来的利润,以及怎么分配。以及由此产生的合作机制。本文则侧重在竞争环境和序贯博弈前提下团购这种营销模式对零售商(卖方)的影响,它会导致零售商们作出怎样的定价策略。
2 模型建立与讨论
2.1 模型假设
①假设两个零售商将某种商品在某市场上销售,其中,零售商1为市场领导者,零售商2是市场跟随者。
②各零售商都是经济理性人。
③零售商定价。本模型采用以下常用的线性反需求函数(Zhang & Liu[13]等)作为零售商的售价表达式:
pi(qi,qj)=Ai-qi-bqji,j∈{1,2}i≠j,0 (1) ④本文中零售商的批发价采用常用的线性批量折扣模型(Ingene和Parry[14]),(qT)=pIP-βqT。 ⑤即使在零售商团购模式下,依然有比例θ的顾客为忠实的传统模式消费者。即有1-θ的顾客选择团购模式消费。同时,团购还会吸引一部分原本不是企业潜在客户的客户参与,即会扩大企业的潜在客户群,但是,这部分扩大的客户只会参与团购这种消费模式。 ⑤u代表引入团购后的额外单位成本,本模型中假设两家零售商额外成本相同。 ⑥c代表零售商的单位运营成本,本模型中假设两家零售商单位运营成本相同。 ⑦A1,A2分别代表两家零售商的市场规模,注:A1>A2。 在没有引入团购时,零售商1作为市场领导者,零售商2作为市场跟随者,零售商2假设零售商1的定价策略后确定自己最优的定价和销售数量。零售商1在后发优势下根据零售商2的策略决定自己的最优策略,据此可得出零售商1和零售商2各自的最优策略,这是一个斯塔克伯格博弈。 两家零售商的利润分别如下: (2) (3) 均衡解如表1所示: 表1 在没有引入团购时的定价策略博弈结果 当市场上引入团购营销模式后,零售商均采取团购营销模式以吸引顾客,零售商的单位销售成本会增加u。在这种情况下,两个零售商会再次进行斯塔克伯格博弈。 团购各方利润: (4) (5) 考虑批量折扣: (6) (7) 均衡解如表2所示。 本部分将通过比较分析团购营销策略对零售商们的影响,在什么情况下零售商愿意引入团购营销方式。特别是在竞争条件下团购活动给双方带来怎样的利润变化。 此结论说明了虽然团购促销活动看似能提高销售量,但因为团购活动会吸引走一部分传统顾客,且团购促销时单位销量的利润更低,故只有当团购活动能吸引到足够多的非潜在顾客时,供应方才愿意引入团购营销活动。 表2 在引入团购时的定价策略博弈结果 其中:X=1-2βθ,Y=1-4βθ。 在团购营销下,两家零售商产品替代度b的变化对零售商各自的影响如下。 对于零售商1而言有: 当b增大即两家零售商竞争较为激烈时,零售商1的销量会随着折扣程度β增加而增加,但是利润会先升后降。这说明,当两家零售商竞争较为激烈时,即便利润下降,零售商1也会加大折扣力度以维持市场占有率。 对于零售商2而言有: 当b增大即两家零售商竞争较为激烈时,零售商2的销量会随着折扣程度β增加而增加,但是利润也会先升后降。这说明,当两家零售商竞争较为激烈时,即便利润下降,处于跟随地位的零售商2也会加大折扣力度以维持市场占有率。但因为零售商2处于跟随地位,即A1>A2,当竞争比较激烈且零售商2原本市场占有就远小于零售商1时,其会有意愿退出团购市场以保证自己的生存。 本部分讨论在团购营销模式下引入团购导致的额外成本对零售商各自的影响。 同理,对于零售商2而言有:零售商2的团购部分销量和常规部分销量均随着u上涨而上涨,但价格下降,利润降低。即在引入团购营销模式后,当零售商之间的竞争较大时,处于跟随地位的零售商则会被动降低价格,牺牲一部分利润来维护市场。此时结果将是两家零售商均会牺牲一部分利润。 当竞争过大且当引入团购带来的额外成本过高时,则会导致其中一家零售商退出团购市场,另一家零售商处于垄断地位。 参照“零售商的斯塔克伯格团购博弈分析”,本文算例讨论中的参数选取如下:b=0.7,A1=1.9,A2=1.4,c=0.15,u=0.08。 由图1可得:当0.25<βθ<0.5时,零售商1和零售商2的团购价格均随单位额外成本u的上升而下降。同时,从图中可以看出,零售商2市场体量较小,对成本上升反应较为敏感。 根据图2:当0.5<βθ<1时,零售商1和零售商2的团购价格均随单位额外成本u的上升而上升。同时,从图中可以看出,此时零售商2的价格升高更为明显。 图1 零售商单位额外成本对团购价格的影响(βθ=0.375) 由图3和图4可得:当0.25<βθ<0.5时,零售商1的团购价格对竞争程度不太敏感,零售商2则对竞争程度比较敏感。当0.5<βθ<1时,零售商2的团购价格则随竞争程度升高而降低。同时,从图中可以看出,零售商2市场体量较小,对竞争程度上升反应较为敏感。这是因为,当折扣程度不足以吸引较多额外客户时,零售商2会因为利润降低而提高售价以保证盈利。但当折扣足以吸引足够多的额外客户时,随着竞争程度增加,为了保证更高的利润,零售商2则会适当降价以吸引更多的潜在客户,而零售商1则因为处于市场领导地位而对其反应平淡或者说其价格对竞争程度不太敏感。 图2 零售商单位额外成本对团购价格的影响(βθ=0.75) 图3 零售商之间的竞争程度b对团购价格的影响(βθ=0.375) 图4 零售商之间的竞争程度b对团购价格的影响(βθ=0.75 ) 由图5和图6可得:当0.25<βθ<0.5时,即当团购打折不足以吸引更多额外顾客时,零售商1和零售商2的团购价格均随着潜在市场差距增大而升高,其中,零售商1的团购价格增高更快,这是因为零售商1处于领导地位,当其市场占有比零售商2大得越来越多的时候,其根据价格控制权,同时也可以通过适当提高价格以扩大利润。零售商2则被动提价。 当0.5<βθ<1时,即团购折扣能带来额外足够多的潜在客户。此时,零售商1随着与零售商2市场差距越来越大而提高团购价格以扩大自己的利润。而零售商2则因为自己市场占有率过小而不得不降低团购价格而保证自己的生存。 注:图中s表示零售商1的潜在市场与零售商2的潜在市场之比,下同。图5 零售商市场占有度(潜在市场大小)对团购价格的影响(βθ=0.375) 图6 零售商市场占有度(潜在市场大小)对团购价格的影响(βθ=0.75) 根据以上讨论,我们可以发现,在市场引入团购这种营销模式后,市场参与各方的利润分配发生了根本性变化。引入团购后,各零售商的团购价格、销售数量均受多方因素影响。 ①在一定范围内,商家销量、定价策略极容易受到团购额外成本的影响,比如,在企业自主组织的团购会所带来的额外成本,如果是通过团购平台则受团购平台的佣金的设定的影响。 ②随着两家零售商的商品同质化程度加深,处于市场跟随者的零售商会受到更大的影响,市场跟随者应该积极做好营销宣传,力争团购吸引更多的额外潜在客户以获得竞争优势;同时,对于小企业来讲,开发差异化产品是获得生存空间并发展的关键。 ③团购这种营销模式虽然能增加零售商的出货量,加快资金回流速度,从而增加零售商的利润,但是,因为其单位利润更低,故而,零售商在引入团购这种营销模式的时候需要综合考虑自己在市场上的地位,即市场占有率,还有团购的额外成本,与竞争者的产品替代程度等因素而综合定价,才能获得更高的整体利润,抢占市场。 本文在讨论的过程中,还存在一些局限。例如:本文假定团购额外成本是已知的(即固定的),但在实际中,企业除采取团购会这种形式以外,更多的情况则是企业依赖于团购平台,即第三方企业,这使得团购额外成本是不可控的,由第三方企业根据自己的利润来制定,即处于跟随地位的企业需要观察处于领导地位的企业的策略来制定自己的策略,同时,两家企业也都需要观察第三方的佣金策略来制定自己的战略,这就形成的一个“二重斯塔克伯格博弈”,在后续的研究中还可以继续跟进。 随着现代营销手段的发展,类似于汽车零售商组织团购会这种营销模式得到逐步的推广,这种团购活动能增加企业的出货量,加快资金周转速度,提升利润等一系列好处。然而,本文通过建立商家的利润函数,尤其是引入团购这种营销模式后,两家具有一定产品替代度的企业在市场中的博弈,通过斯塔克尔伯格数量博弈分析,求出均衡解,得出各自的销量,定价策略。并由此发现,团购这种营销模式并不总是能给所有零售商都能带来利润的增长。零售商各自的潜在市场规模、产品替代度以及团购额外成本等都能直接影响零售商们的利润。就汽车销售行业而言,由于许多汽车生产厂商实力各不相同,很多终端销售又是由生产厂家控制,因此会在特定的条件下出现团购会并不能给实力太过弱小的企业增加利润这种情况。这也直接导致部分弱小的企业可能会和大企业间的差距越来越大,直至被淘汰出局。2.2 符号说明
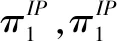



2.3 没有引入团购时的竞争环境下的零售商定价策略

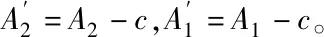
2.4 在竞争环境下的团购博弈模型
2.5 引入团购前后比较


2.6 团购营销模式下产品替代度b的影响
2.7 团购营销模式下团购额外成本的影响
3 算例讨论
3.1 βθ和单位额外成本u对团购价格的影响

3.2 βθ和竞争程度b对团购价格的影响



3.3 βθ和市场占有度A对团购价格的影响
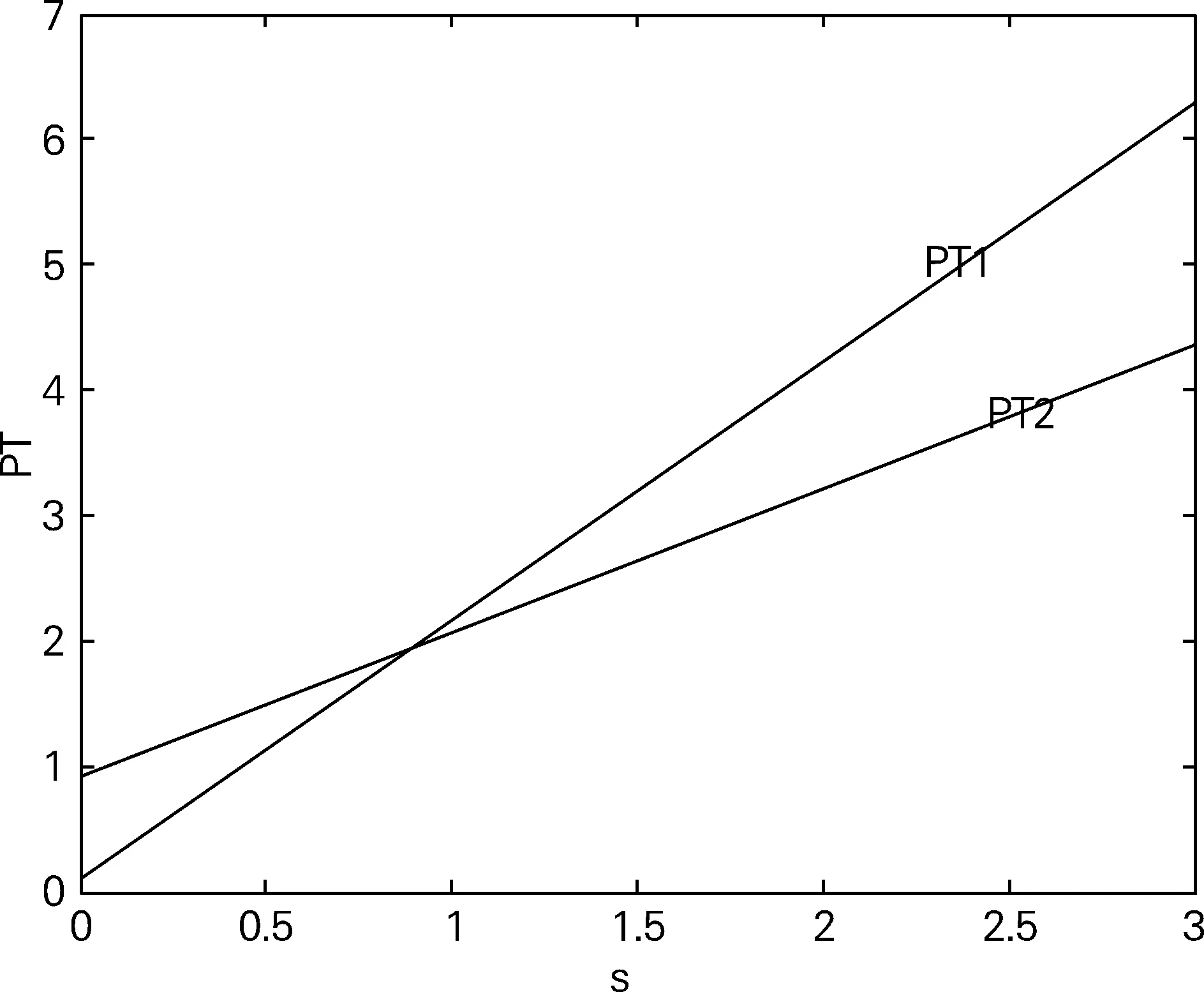

3.4 讨论
4 结束语

