一次侧凝结对间接蒸发冷却换热性能的影响

郭春梅,刘起隆,李 岩,由玉文,吕 建

(天津城建大学 能源与安全工程学院,天津 300384)

0 引 言

传统的直接蒸发冷却(Direct Evaporative Cooling,DEC)技术因其在对干空气降温的同时使空气含湿量增加而在高温干燥地区得到广泛应用[1]。间接蒸发冷却(Indirect Evaporative Cooling,IEC)技术在对干空气冷却的过程中不增加空气的含湿量,但可提供更高的室内热舒适性而被应用于更广泛的地区。

MACLAINE-CROSS等[2]利用类比法,将换热壁面存在液膜的换热器与传统无液膜覆盖的空气-空气换热器进行类比,提出一种线性相关的理论模型来求解计算间接蒸发冷却器的传热传质性能。STOITCHKOV等[3]在文献[2]理论模型的基础上,通过计算喷淋液膜平均温度以及总换热量与显热换热量的比率修正了求解的间接蒸发冷却传热效率。文献[4-7]通过假设空气温度与焓值之间成线性变化关系,重新定义了间接蒸发冷却中所涉及到的部分参数,利用效能传热单元数法(ε-NTU)对间接蒸发冷却传热传质过程进行计算求解。HEIDARINEJAD等[8]在对叉流板式间接蒸发冷却传热传质过程的研究中,考虑了换热壁面的导热过程以及二次侧通道换热壁面上不同的液膜温度,提出新的理论计算模型,并利用有限差分的方法对理论模型进行求解计算。REN等[9]针对平行流动及逆向流动的间接蒸发冷却传热传质过程进行了分析,推导出一维微分方程计算其传热传质性能,并在理论模型中引入不同的刘易斯数及二次侧通道内壁面的湿润度。并采用火用分析的方法研究间接蒸发冷却传热传质过程中能量及有用能之间的转化关系,证实了湿空气火用作为间接蒸发冷却潜力的合理性[10]。CUI[11]对用于计算显热换热器传热性能的平均温差法进行修正,加入了潜热换热的数学表达式,应用于间接蒸发冷却传热传质过程,计算结果与实验测试结果之间最大误差为8%。CHEN[12]在文献[9]的基础上,建立了一种基于效能传热单元数法(ε-NTU)简化计算的一维逆流板式换热理论模型,研究间接蒸发冷却换热系统中一次侧换热通道在无凝结、部分凝结及全部凝结3种不同状态时的换热情况。之后，通过数值求解分析一、二次侧空气温湿度、空气流速、换热器间距、换热器尺寸以及二次侧换热壁面湿润度对平行流动/逆向流动的间接蒸发冷却换热器性能的影响,并对各影响参数进行了敏感性分析[13-14]。郑斌等[15]在文献[12-14]基础上,通过对一次侧能量和质量平衡方程中引入凝结面积比(σ)的方法,建立了二维叉流间接蒸发冷却传热传质模型。本文在此基础上研究了一次风通道中非凝结(σ=0)、全部凝结(σ=1)和部分凝结(0<σ<1)3种凝结状态与凝结面积比的判断和求解方法,并研究了凝结面积比对换热性能的影响。

1 模型建立

为便于计算，文中所涉及各变量见表1。

表 1 各变量

1.1 物理模型

冷却器的长度为L、高度为H,气流通道宽度为W。在叉流间接蒸发冷却器内,一次风(空调新风)水平流动,二次风(空调排风)自下而上垂直流动,两股气流通过换热壁面进行分隔。喷嘴将水分散成细小的水滴,与二次风逆向流动,自上而下均匀地喷淋在二次侧壁面。一次风侧,当新风的露点温度高于壁面温度时,则产生凝结液膜。建立二维传热传质微元体的长度和高度分别为dx、dy。物理模型如图1所示。

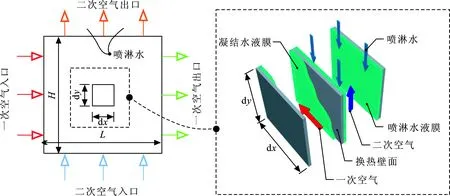
图 1 间接蒸发冷却物理模型Fig.1 Physic model of indirect evaporative cooling

1.2 数学模型

1.2.1 数学模型的简化与假设 ①假设传热传质过程为稳态过程;②换热器表面做隔热保温处理,假设表面为绝热边界;③忽略沿壁面纵向热传导以及沿流动方向的流体内部热传导;④忽略换热壁面沿水平方向的导热过程;⑤水-空气系统的lewis数为常数1。⑥假设喷淋液膜均匀覆盖整个换热壁面,厚度均匀一致;⑦假设在产生凝结液膜的壁面上,凝结液膜均匀覆盖,厚度均为0.35 mm[16]。⑧由于喷淋水液膜及空气凝结液膜厚度非常薄,忽略液膜内部的对流换热影响。

1.2.2 传热传质过程平衡方程 根据间接蒸发冷却传热传质过程的物理模型,建立质量及能量平衡方程,公式(1)～(7)依次为一次侧空气传热传质过程能量平衡方程、一次侧空气凝结过程质量平衡方程、二次侧空气对流传热传质换热过程能量平衡方程、二次侧空气蒸发过程质量平衡方程、一次侧换热壁面上凝结液膜传热传质过程能量平衡方程、二次侧换热壁面上喷淋水液膜传热传质过程能量平衡方程、换热壁面传热过程能量平衡方程。

h1(Tpl-T1)(1-σ)dxdy+

rhm1(ω1,w-ω1)σdxdy

(1)

(2)

rhm2(ω2,w-ω2)dxdy

(3)

(4)

[h1(Tc-T1)σdxdy+

rhm1(ω1,w-ω1)σdxdy]

(5)

[h2(Tw-T2)dxdy+

rhm2((ω2,w-ω2)dxdy]

(6)

(7)

上述公式中,合成参数湿空气焓值i、含湿量ω、对流传热系数h、传质系数hm的计算过程分别为

i=cpT+ωr

(8)

ω=aT+b

(9)

空气温度在20～40 ℃变化时,A=0.001 445 8,B=-0.015 525

(10)

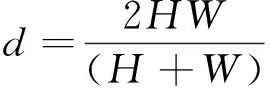
(11)

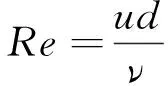
(12)

式中：Re为雷诺数。

根据传热传质类比法,在空气-水界面上:

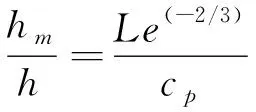
(13)

喷淋液膜的厚度可根据喷淋水量和Nusselt经验公式计算[1],即

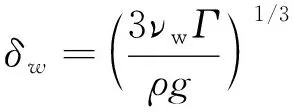
(14)

(15)

(16)

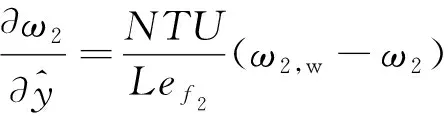
(17)

(Tpl-T1)(1-σ)]

(18)

(19)

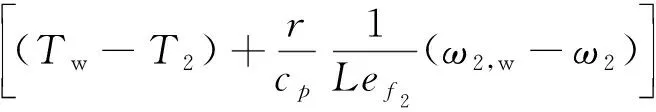
(20)

(21)

k1,pl(T1-Tpl)(1-σ)]-

kw,pl(Tpl-Tw)}

(22)

上式中,部分参数定义如下:

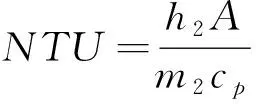
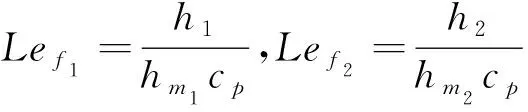
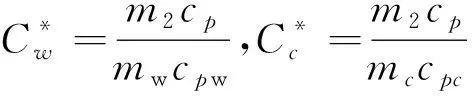
1.2.4 边界条件 间接蒸发冷却传热传质过程控制方程组中边界条件设置为

2 数值求解

利用MATLAB中的Partial Differential Equation Toolbox及有限元分析方法(Finite Element Method,FEM)进行编程求解计算。

利用计算机数值求解过程中,将间接蒸发冷却器换热壁面设置成一个边长为1的正方形,并将其划分成若干个微元。为验证微元尺寸的大小不影响计算结果,首先设置微元尺寸为0.1,0.05,0.025,0.01,0.005等5种情况。在保证计算结果不受微元尺寸大小影响,且具有较高计算机运行速度的情况下,本文在求解计算中将微元尺寸设置为0.025。

通过计算机求解,可分别得到一、二次侧空气温度、含湿量的分布以及换热通道内喷淋水液膜、凝结水液膜和换热壁面的温度场分布状态。

2.1 凝结面积比

当夏季炎热潮湿,新风的露点温度高于间接蒸发冷却器壁面温度时,则会在一次侧壁面发生凝结。凝结面积比(σ)即为新风通道壁面产生凝结液膜的面积占新风通道总换热壁面面积的比例,代表了间接蒸发冷却器内新风侧凝结过程发生的程度,其数值在0～1之间。凝结现象出现在整个换热壁面上,σ=1,为全部凝结状态;反之,在换热壁面将没有凝结现象出现时,σ=0,称为无凝结状态;而当新风的温湿度并不是很高,在进入冷却器后,不会立即出现凝结现象,而是随着换热过程的进行,当换热器壁面温度低于空气的露点温度时,才会出现凝结现象,则称为部分凝结状态,0<σ<1。

2.2 凝结状态的判定与凝结面积比的求解

通过数值计算可得到换热器内一次侧空气含湿量分布。与一次侧入口空气含湿量大小进行对比，若该点一次侧通道内空气含湿量小于入口值,则表明此处换热壁面存在凝结,并作为凝结状态的判定方法。

求解时,首先可假设换热器一次侧通道内无凝结,即凝结液膜面积比为零(σ=0)。若计算结果与假设相符,则可判定为无凝结状态。若计算结果与假设值误差大于计算误差要求,则重新假设为全部凝结状态(σ=1),再次进行计算求解。若计算结果与假设一致,则可判定为全部凝结状态。若计算结果与假设不符,则可判断换热器内凝结状态为部分凝结。并根据前两次假设条件下的计算结果合理假设凝结液膜面积比,将求解得出的凝结液膜面积比与假设值进行对比。当求解值与假设值之间的误差满足计算误差要求,则可认为假设的凝结状态以及凝结面积比正确,若两者之间误差超过计算误差允许范围后,需重新假设凝结状态进行计算,直到计算结果与假设值在精度要求内相符合,即可得出部分凝结状态下的凝结面积比。间接蒸发冷却传热传质控制方程组的求解流程,如图2所示。

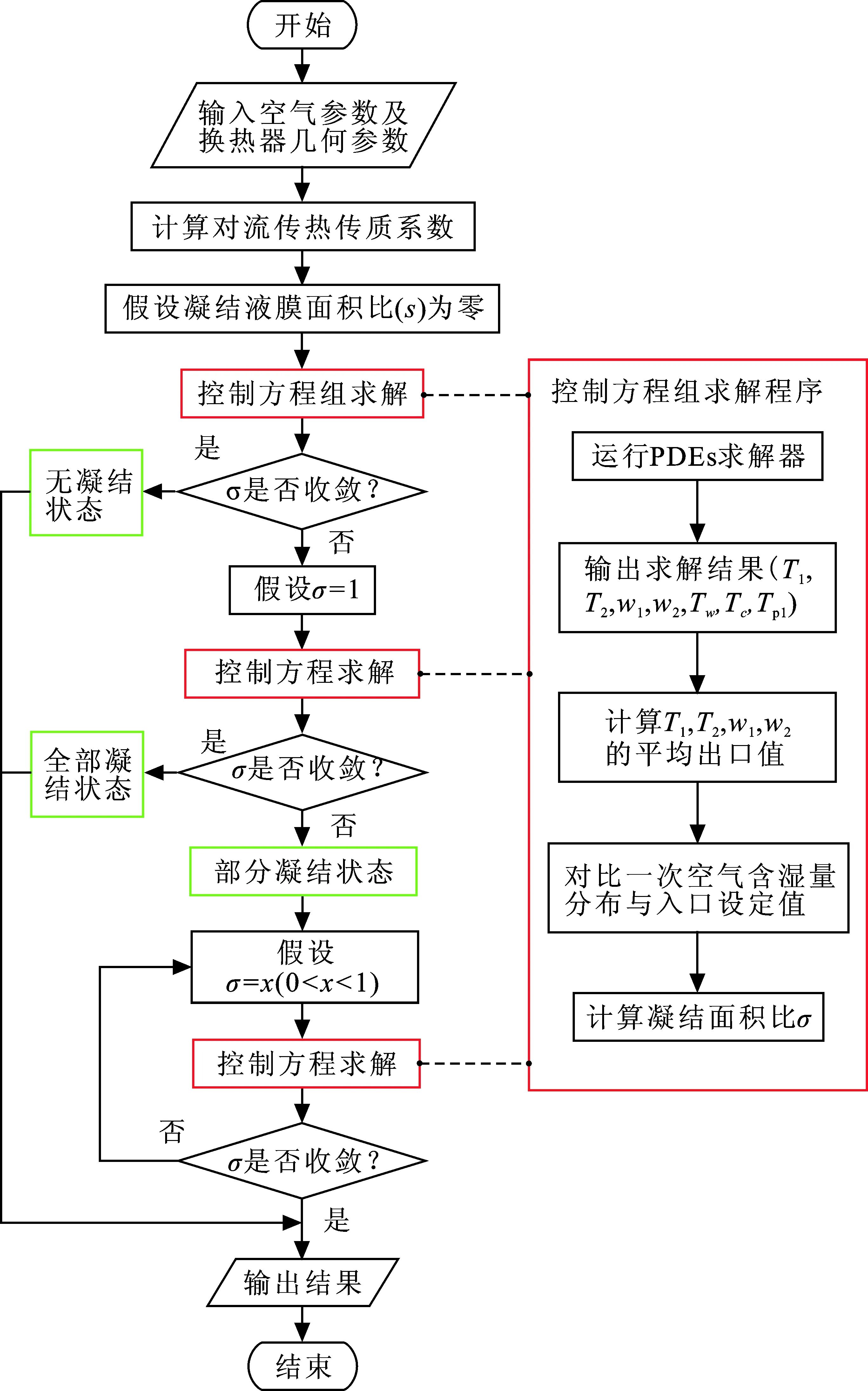
图 2 数值求解流程图Fig.2 Flowchat of numerical solution

2.3 数值模拟工况与参数设置

在研究一次侧凝结对间接蒸发冷却传热传质过程的影响时,二次侧空气为空调排风,温湿度恒定为25 ℃,50%。夏季室外新风入口温度变化范围28 ℃～38 ℃(间隔为1 ℃),相对湿度则设定为30%,50%,70%,90%等4种状态。

换热器的几何尺寸及空气流量与喷流水量等参数的设置与实验系统一致,实验系统、测试仪器仪表及实验测试误差的分析见文献[17],其参数设置如表2所示。

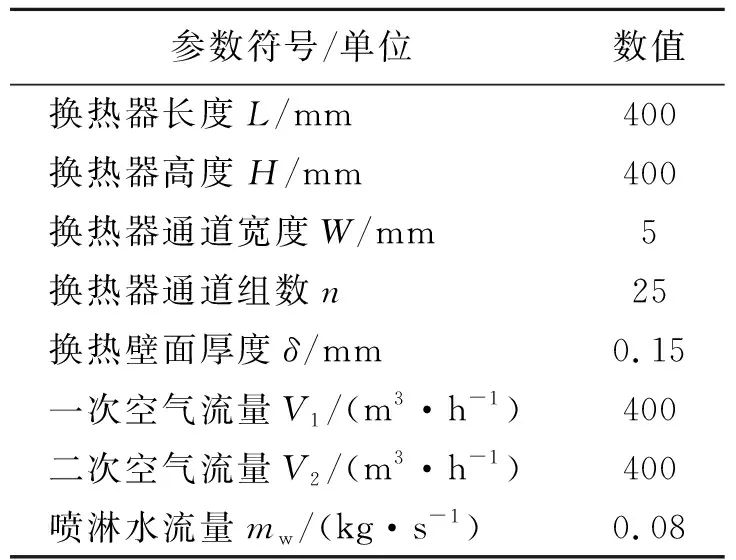
表 2 数值求解参数设置

2.4 理论模型的实验验证

图3(a),(b)分别表示一次侧空气出口温度和含湿量的数值计算结果与实验测试的对比结果。在相对湿度分别为30%,50%,70%,90%的4种工况下,一次侧空气出口温度的理论计算结果与实验测试值的最大偏差为8.6%。一次侧出口空气含湿量的计算结果与实验测试结果具有较高的一致性,最大偏差仅为6.6%。表明了该理论模型计算结果的可靠性,可以利用该理论模型研究在不同凝结状态下间接蒸发冷却的传热传质过程。

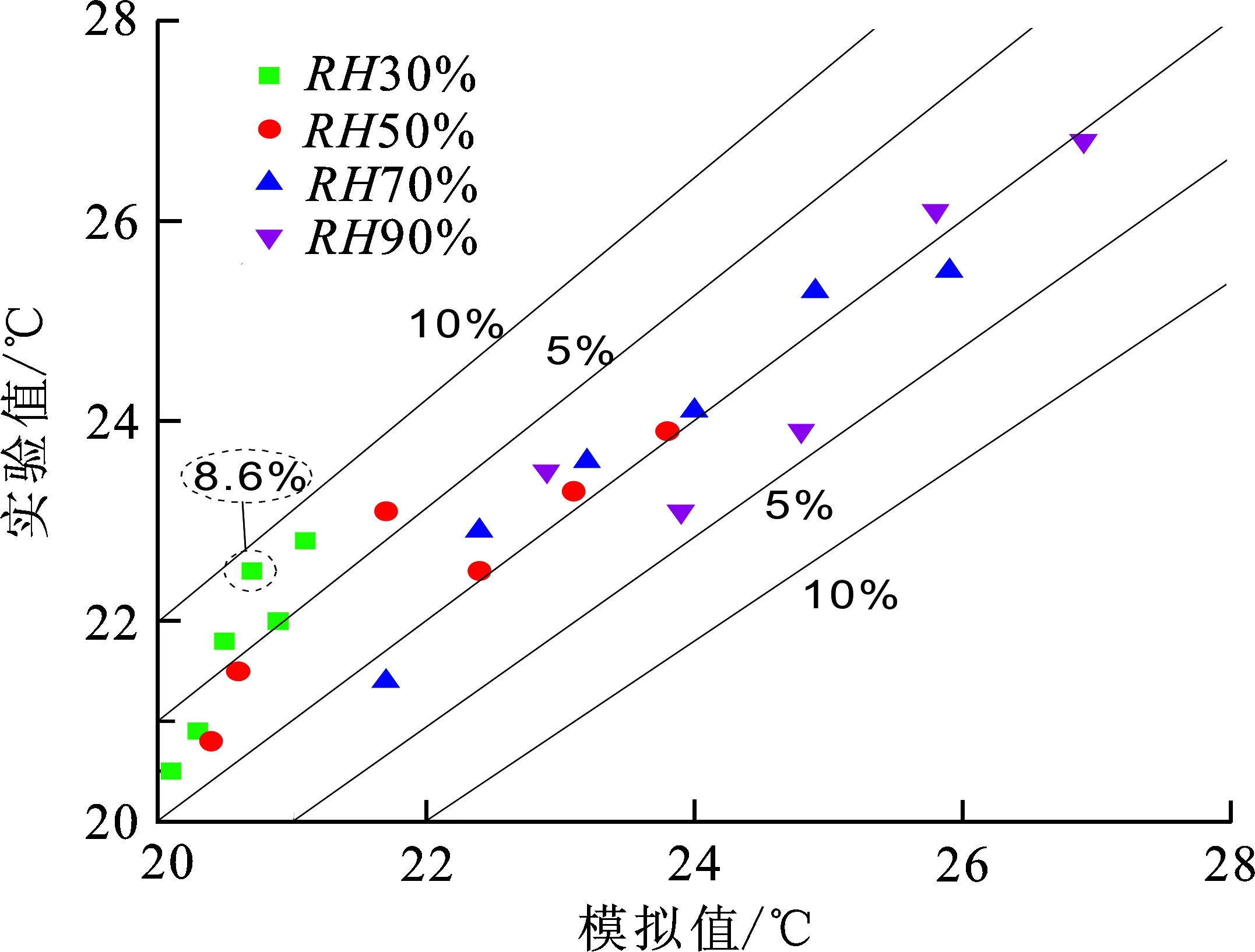
(a) 一次空气出口温度

(b) 一次空气出口含湿量图 3 理论模型数值计算结果与实验结果对比

3 数值模拟结果与分析

3.1 对湿球效率的影响

湿球效率为一次侧空气进出口温差与一次侧空气入口干球温度和二次侧空气入口湿球温度差的比值,即

(23)

图4表示了模拟工况与一次侧新风通道产生的凝结液膜面积比。在RH=30%,T≥28 ℃和RH=50%,28 ℃≤T≤31 ℃时,σ=0,为非凝结状态;在RH=90%,T≥28 ℃工况下,σ=1,为全部凝结状态;其他工况下,均为部分凝结状态,0<σ<1。

图4同时表明了凝结面积比与湿球效率的关系。σ=0时，随着一次空气温度的升高，湿球效率逐渐升高,变化范围在78%～84%之间;σ=1时,湿球效率随着一次空气温度的升高呈较小幅度的下降,在48%～51%范围内变化,对比不凝结状态下降约30%;0<σ<1时,随着一次空气入口温度、湿度的升高,凝结面积比与增大,湿球效率下降。其中当一次侧空气入口相对湿度高于50%,一次侧空气温度升高至31 ℃时,凝结液膜面积比将由0逐渐升高至0.65,湿球效率从82%降至70%,变化幅度最为明显。在T=28 ℃时,RH=30%,50%,70%,90%,凝结面积比σ=0，0，0.71，1.0,湿球效率分别为77%,77%,62%,51%。可见,湿球效率与凝结面积比成负相关,凝结面积比增大,湿球效率下降。

图 4 凝结面积比与湿球效率的关系Fig.4 The relation of condensation area ratio and wet-bulb efficiency

3.2 对系统除湿率的影响

除湿率为一次侧空气进出口含湿量的差值与入口空气含湿量的比值,即

(24)

图5为模拟工况下除湿率的变化曲线,除湿率随一次风入口温度、湿度的升高而升高;在一次风入口温度T=38 ℃,RH=90%时,除湿率达到最大值,为48%。

图 5 除湿率的变化曲线Fig.5 Curve of dehumidification rate

对比模拟工况与σ的关系时,得到除湿率与σ的关系。在σ=0时，一次侧空气在换热过程中的含湿量保持不变,除湿率为0。0<σ<1时,除湿率与σ成正比,凝结面积比增大,除湿率提高。

3.3 对换热量的影响

系统的显热与潜热换热量的变化如图6所示,总换热量的变化如图7所示。根据模拟工况下的σ变化情况得到，σ=0时，显热换热量最大,且随着温度的升高自1.1 kW增加到2.1 kW,潜热换热量为0,系统总换热量最低，其数值等于显热换热量;σ=1时,显热换热量最低,随着温度的升高自0.7 kW增大至1.3 kW,潜热换热量和总换热量最大,随着温度的升高而增大,分别为1.9 kW～5.1 kW和2.6 kW～6.4 kW,潜热换热占73%～79%,其他工况下为部分凝结状态;0<σ<1,潜热换热量、总换热量随着σ的增大而增大,显热换热则相反,逐渐降低。

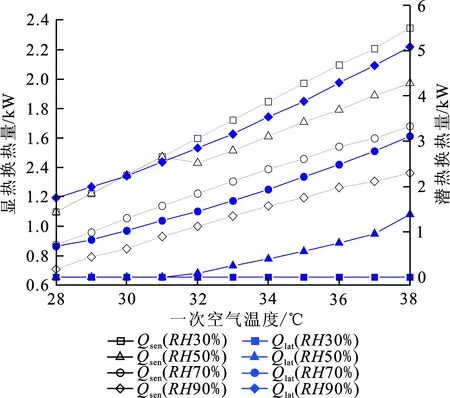
图 6 对显热换热量及潜热换热量的影响Fig.6 Effect on sensible heat transfer and latent heat transfer

图 7 对总热换热量及放大系数的影响Fig.7 Effect on total heat transfer and enlargement coefficient

3.4 对放大系数的影响

放大系数为间接蒸发冷却过程中的总换热量与显热换热量之比,即

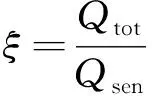
(25)

如图7所示,σ=0时,放大系数恒为1;σ=1时,放大系数变化范围3.7～4.9;0<σ<1,放大系数随着σ的增大而增大。

4 结 论

(1) 提出非凝结(σ=0)、全部凝结(σ=1)和部分凝结(0<σ<1)3种凝结状态与凝结面积比的判断和求解方法。模拟结果与实验数据有较好的吻合性,一次侧空气出口温度、湿度的理论计算结果与实验测试值的最大偏差分别为8.6%和6.6%。

(2) 在模拟工况下,凝结面积比的变化范围为0≤σ≤1,湿球效率则从84%降低至48%。湿球效率与凝结面积比成负相关,凝结面积比增大,湿球效率下降。

(3) 系统除湿率与凝结面积比成正比,凝结面积比增大,除湿率提高。

(4) 凝结面积比对系统潜热换热量、总换热量和放大系数的影响为正相关,而对显热换热的影响则为负相关。

(5) 在全部凝结状态下,放大系数变化范围3.7～4.9,其中潜热换热量占总换热量的比例为73%～79%,节能效果显著。