SLCE 序列的2-adic 复杂度

王艳，李顺波，薛改娜

（西安建筑科技大学理学院，陕西 西安 710055）

1 引言

周期伪随机序列在通信和密码领域有着广泛的应用。有关周期序列的自相关性、线性复杂度及2-adic 复杂的研究一直是序列研究的热点。

周期序列可以由线性移位寄存器(LFSR，linear feedback shift register)生成，也可以由带进位的移位寄存器(FCSR，feedback with carry shift register)生成。生成序列的最短LFSR 的级数称为该序列的线性复杂度，生成序列的最短FCSR 的级数称为该序列的2-adic 复杂度。由B-M (Berlekamp-Massey)算法和有理逼近算法可知，获得连续2 倍线性复杂度或2 倍2-adic 复杂度长的序列，便可以恢复生成该序列的LFSR 或FCSR，因此，周期序列的设计要求高线性复杂度、高2-adic 复杂度。同时，序列的自相关性也是衡量序列的一个重要指标，好的序列应该有低的自相关值。

SLCE (Sidelnikov-Lempel-Cohn-Eastman)序列是一类偶周期分圆序列，由Sidelnikov[1]首次提出，故有文献称该类序列为Sidelnikov 序列；Lempel、Cohn 和Eastman[2]研究了该类序列的自相关性，使该序列受到关注，因而很多文献中以这4 人的姓名首字母的缩写（SLCE）命名这种分圆序列。SLCE序列的线性复杂度一度是一个难题，Kyureghyan 等[3]发现SLCE 序列的线性复杂度与一类分圆数的余数及 Jacobsthal 和有关，推进了此项研究工作。Helleseth 等[4-5]给出了p=3,5,7 时，周期为pm-1 序列的线性复杂度；Meidl 等[6]利用分圆数确定了某些具体序列的线性复杂度。之后关于SLCE 序列1-错线性复杂度[7]、线性复杂度的界[8-9]、特征值[10]等研究陆续出现。基于这些研究，SLCE 序列的2-adic 复杂度也成了一个有意义的问题，本文主要研究SLCE 序列的2-adic 复杂度。

2 基础知识

2.1 SLCE 序列

设q为奇素数p的幂，即q=pm，记Fq为q元有限域，α为Fq的本原元，即Fq的乘法群的生成元。定义中的二次特征为

设q=df+ 1，〈αd〉为由αd生成的乘法子群，称陪集为关于Fq的d阶分圆陪集。显然此处依赖于α的选择，于是有

引理1[11]若q≡ 1(mod4)，则有

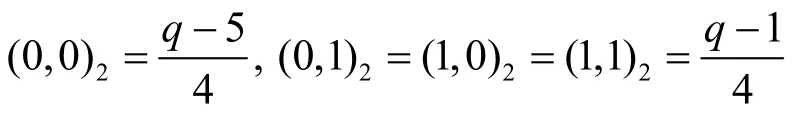
若q≡ 3(mod 4)，则有

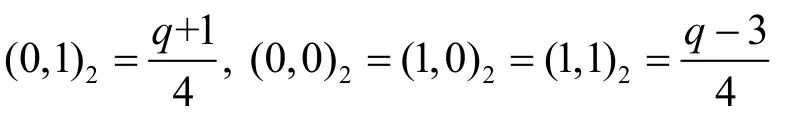
由前述记号，在上定义周期为(q-1)的SLCE序列{si}如式(1)所示。

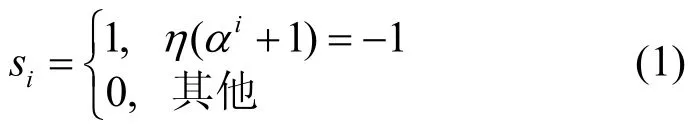
称序列{si}为SLCE 序列。这个定义等价于

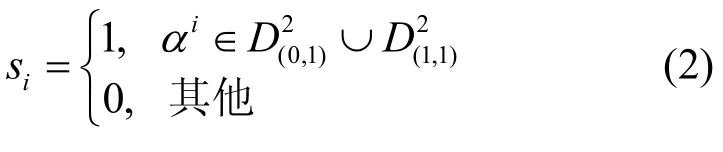
也等价于

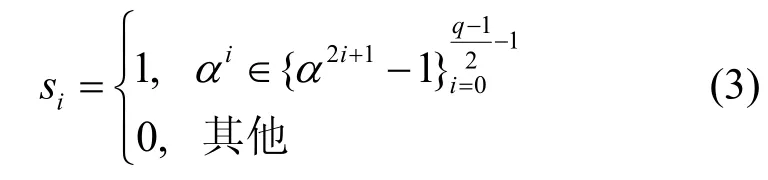
根据式(2)，在有限域F31中取本原元α=3，d=2，则有

进而可得一个周期为30 的SLCE 序列如式(5)所示。

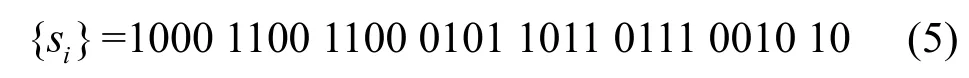
2.2 FCSR 和序列的2-adic 复杂度

考虑到线性移位寄存器容易被攻击的问题，Klapper 等[12]提出了自带进位的反馈移位寄存器(FCSR)。FCSR 由r个系数qi(i=1,2,…,r）∈(0,1),qr=1，以及一个初始存储整数mn-1(可为任意整数)确定，结构如?图1 所示。

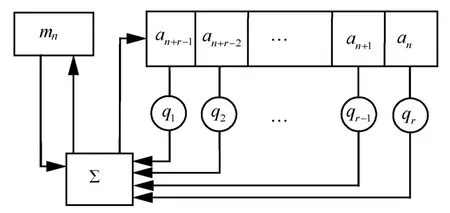
图1 FCSR 结构

记FCSR 的任意一个状态为 (an-1,an-2,…,ai,…,an-r)(ai∈{ 0,1},i=n-1,n-2,…,n-r)，存储整数为mn-1，其运算如下。

2)右移一位，输出最右端的an-r。

3)将a n=δn(mod2)放入FCSR 最左端。

每一个最终周期序列都可以由一个 FCSR 产生。反过来，所有由FCSR 生成的序列也都是最终周期序列[12]。设为最终周期序列，q为生成的FCSR 的连接整数，则称q为的极小连接整数，极小连接整数整除任意连接整数。FCSR 序列的周期完全由其极小连接整数确定。类似于线性复杂度，2-adic 复杂度衡量一个周期序列需要用多大周期的FCSR 来生成，定义如下。

定义 1[12]设s={si}为严格周期序列，其中，q为序列s的极小连接数，整数p满足gcd(p,q)=1，称实数ϕ(s)=lbq为序列s的2-adic 复杂度。

2-adic 复杂度衡量一个二元序列由带进位的移位寄存器(FCSR)[12-13]生成的难度，它与线性复杂度没有必然联系。具有高线性复杂度的序列的2-adic复杂度可能会很低，反之亦然。Klapper 和Goresky[12]提出了有理逼近算法，即对于一条固定序列，只要已知其约为2-adic 复杂度个位置上的元素的2 倍，就能唯一确定原序列。这就要求密钥序列必须具有高的2-adic 复杂度，才能有效抵抗有理逼近攻击。

设s为严格周期序列，记则有，故

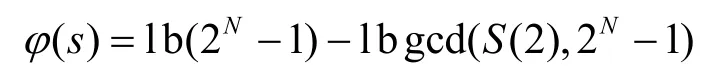
当gcd(S(2),2N-1)=1时，ϕ(s)达到最大值l b(2N-1)≈N。

巧合的是，2N-1=MN恰为第N个Mersenne数，当MN为 Mersenne 素 数 时，有gcd(S(2),2N-1)=1，即序列s的极小连接整数为Mersenne 素数时，其2-adic 复杂度达到最大。迄今，已发现的Mersenne 素数有51 个，分别为N=2,3,5,7,13,17,19,31,61,89,107,127,521,607,1 279,2 203,2 281,3 217,4 253,4 423,9 689,9 941,11 213,19 937,21 701,23 209,44 497,86 243,110 503,132 049,216 091,756 839,859 433,1 257 787,1 398 269,2 976 221,3 021 377,6 972 593,13 466 917,20 996 011,24 036 583,25 964 951,30 402 457,32 582 657,37 156 667,42 643 801,43 112 609,57 885 161,74 207 281,77 232 917,82 589 933。由于第N个Mersenne 数为素数的必要条件是N为素数，因而对素数周期序列，当周期N满足2N-1 为素数时，序列2-adic 复杂度达到最大。

对一般周期序列，2-adic 复杂度由gcd(S(2),2N-1)确定，这依赖于序列本身的性质。Tian 等[13]研究了m序列的2-adic 复杂度，利用m序列极小多项式的特征，推导出m序列可以达到最大2-adic 复杂度。Xiong 等[14]通过对周期序列的循环行列式非奇异性的研究，指出任何周期为N的理想二值自相关序列的2-adic 复杂度就是N，该结果覆盖了文献[13]的结果。Hu 等[15]对文献[14]的结果给出了一个简化的证明，给出了获得周期序列2-adic 复杂度的新方法。

3 SLCE 序列的自相关性

设{si},i=0,1,…,n-1，为二元序列，称函数

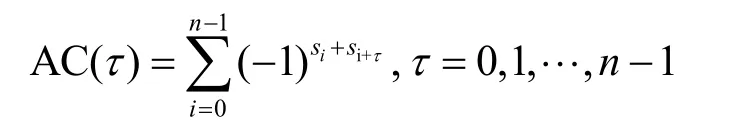
为该序列的自相关函数。周期为n的序列{si}的自相关函数可用差集表示为[16]

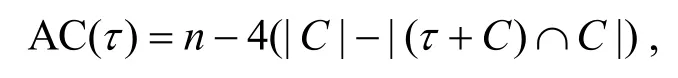
其中，集合C={i|si=1,i=0,1,…,n-1}为序列{si}的支撑集。

由于SLCE 序列为周期为(q-1)的平衡序列，其自相关函数满足

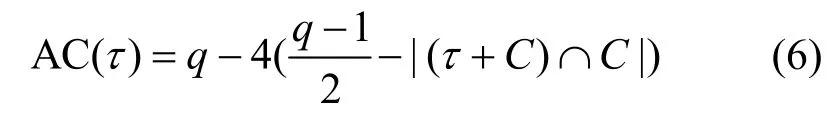
自相关函数值反映了序列在移位τ后，与原序列的接近程度。实际应用中希望序列的自相关函数值尽可能小。

设q为奇素数的幂，即q=pm，记Fq为q元有限域，α乘法群的本原元。记

定理1设{si}是周期为(q-1)的SLCE 序列，则

1)当q≡ 1(mod4)时，

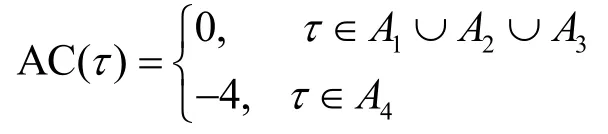
2)当q≡ 3(mod4)时，

证明根据式(1)，需计算|(τ+C)∩C|，定义αC={αi:i∈C}=D1-1，及αC+τ=ατ(D1-1)，则有

由引理1 和式(1)可得

1)当q≡ 1(mod4)时，若τ∈A1∪A2∪A3，则有

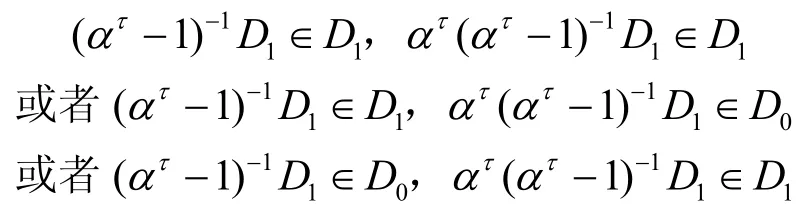
对应的|(τ+C)∩C|分别等于二阶分圆数(1,1)2、(1,0)2和 (0,1)2，且都等于根据式(6)有

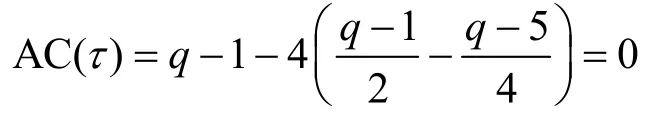
若τ∈4A，则有

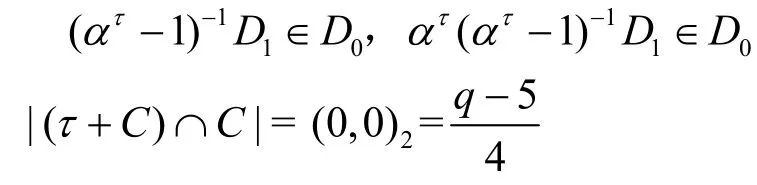
于是

2)当q≡ 3(mod4)时，若τ∈A1∪A2∪A4，则有

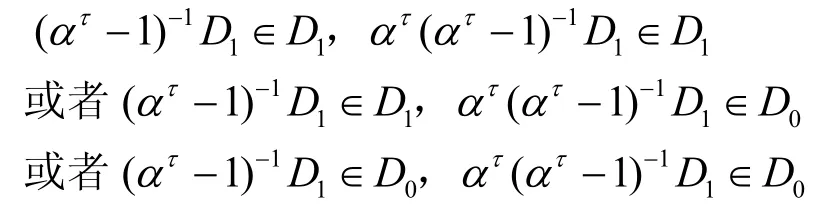
对应的|(τ+C)∩C|分别等于 (1,1)2、(1,0)2和(0,0)2，且都等于。根据式(6)有

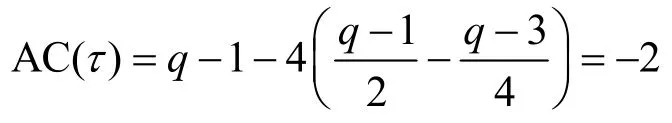
若τ∈3A，则有

于是

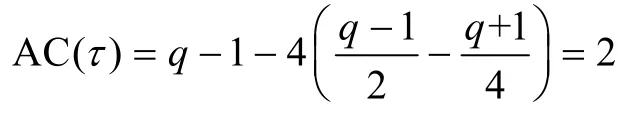
证毕。

定理1 表明SLCE 序列是3 值自相关序列。

推论1设{si}是周期为q-1的SLCE 序列，则

1)当q≡ 1(mod4)时，在τ=1,2,…,q-2中有个数使AC(τ)=-4 。

2)当q≡ 3(mod4)时，在τ=1,2,…,q-2中有的数使AC(τ)=2。

由分圆数的取法可证明推论1。

定义2若序列{si}、{tj}均为周期为N的序列，并且在一个周期上有si=tN-1-i,i=0,1,…,N-1，则称{si}、{tj}为互反序列。

定理2记ϕ为欧拉函数，域Fq中共有ϕ(q-1)个SLCE 序列，并成对为互反序列。

证明由qF中本原元的个数为ϕ(q-1)可得,由于在有限域中，当α为本原元时，α-1也为本原元，故ϕ(q-1)个本原元成对出现。由于对本原元α，时，故α-1生成序列的第i个元与α生成序列的第(q-1-i)个元一样，即为互反序列。

证毕。

定理3设{si}是周期为(q-1)的SLCE 序列，则

1)当q≡ 1(mod4)时，Fq上的全部SLCE 序列共有个自相关谱。

2)当q≡ 3(mod4)时，F q上的全部SLCE 序列共有个自相关谱。

证明记α为Fq的一个本原元，当q≡1(mod4)时，-α也是Fq的一个本原元，且有，故α与α-生成序列的自相关谱相同。又由自相关函数的对称性及α与α-1生成序列为互反序列可知，α与α-1生成序列的自相关谱相同。于是α、-α、α-1、-α-1生成的序列同自相关谱。并且由其他本原元生成序列不同可得，当q≡ 1(mod4)时，F q上的全部SLCE 序列共有个自相关谱。

当q≡ 3(mod4)时，对本原元α、-α不是本原元，由前述知，此时Fq上的全部SLCE 序列共有个自相关谱。

证毕。

下面研究SLCE 序列的2-adic 复杂度。

4 SLCE 序列的2-adic 复杂度

定理4设{si}是周期为(q-1)的SLCE 序列，则

1)当q≡1(mod4)时，

2)当q≡ 3(mod4)时，

证明设{si}为SLCE 序列，记Z[x]多项式为

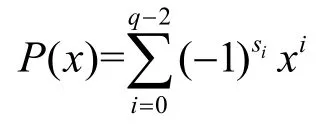
则有

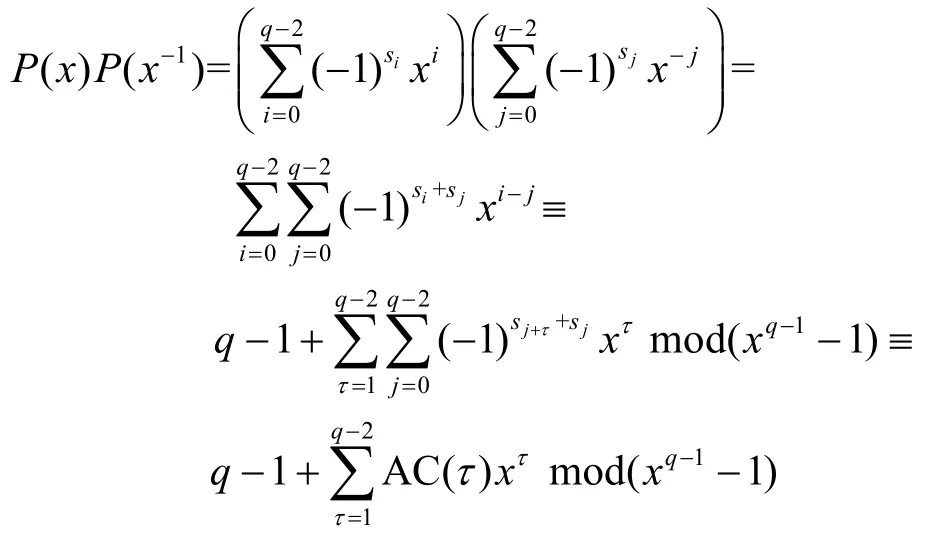
当x=2 时，有

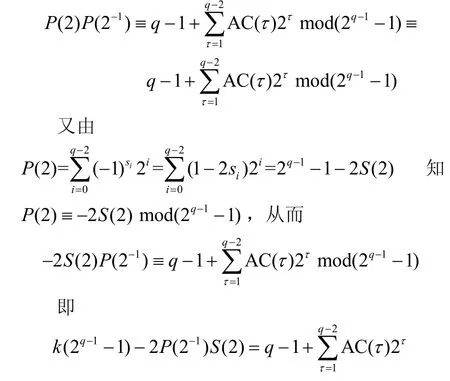
其中，k为整数。于是

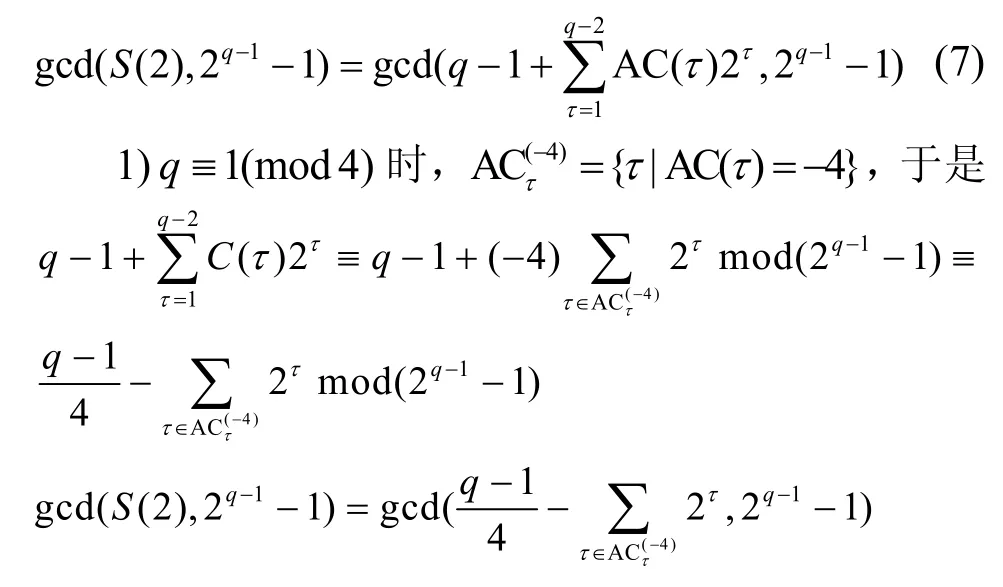
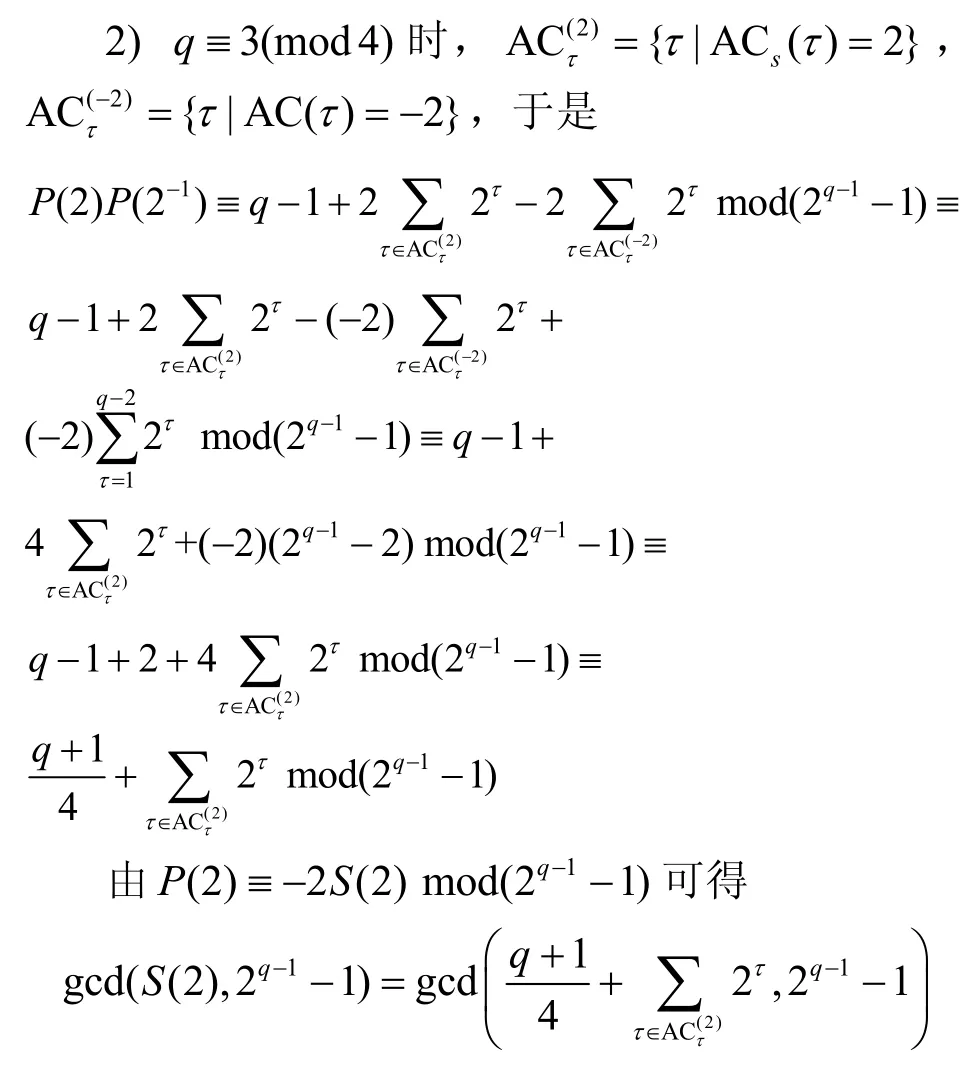
证毕。

推论2 设s={si}是周期为q-1的SLCE 序列，记，有

1)若q≡ 1(mod4)且

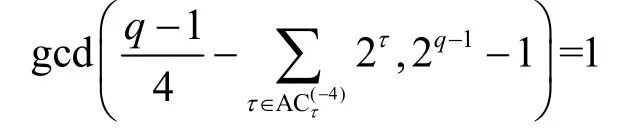
则s的2-adic 复杂度ϕ(s)达到最大值。

2)若q≡ 3(mod4)，且

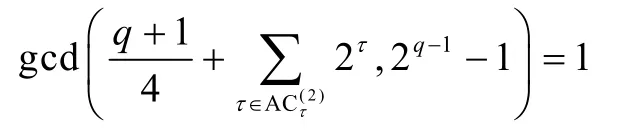
则s的2-adic 复杂度ϕ(s)达到最大值。

推论2 的证明由定理4 易得。

进一步，当q≡ 1(mod4)时，有

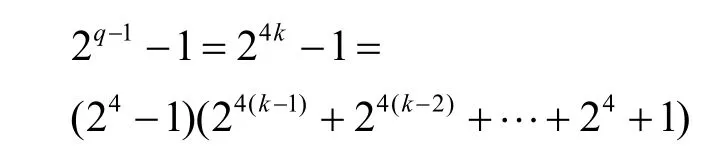
当q≡ 3(mod 4)时，有

例q=43时，F43上的本原元分别对应3,29,5,26,12,18,19,34,20,28,30,33。由本原元3 生成的SLCE 序列为1,0,0,1,1,1,1,0,1,1,0,0,1,0,1,0,0,1,0,1,0,0,0,0,0,0,0,1,1,1,1,1,0,0,1,1,1,0,1,0,0,1。，且有

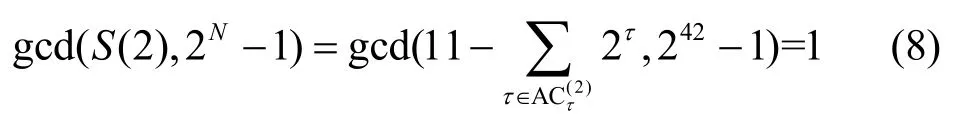
由本原元5 生成的SLCE 序列为1,0,1,0,0,1,0,0,0,0,0,0,1,1,1,0,0,1,1,0,1,0,1,1,1,0,0,1,1,0,1,1,0,1,0,1,0,0,0,1,1,1,，且有式(8)成立。

由本原元26 生成的SLCE 序列为1,1,1,1,0,0,0,1,0,1,0,1,1,0,1,1,0,0,1,1,1,0,1,0,1,1,0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,，且有式(8)成立。

由本原元29 生成的SLCE 序列为1,1,0,0,1,0,1,1,1,0,0,1,1,1,1,1,0,0,0,0,0,0,0,1,0,1,0,0,1,0,1,0,0,1,1,0,1,1,1,1,0,0],且有式(8)成立。

由Magma 验证发现，F43中的所有SLCE 序列都达到最大2-adic 复杂度。类似地，F7、F19、F31、F47等域上的SLCE 序列都可达到最大2-adic 复杂度。但等域上的SLCE 序列都满足gcd(S(2),2N-1)=3。尽管没有达到最大2-adic复杂度，但由可知，在N＞4 时,这样的SLCE 序列仍有很高的2-adic 复杂度。

5 结束语

SLCE 序列已被证明具有高线性复杂度，其2-adic 复杂度取值成为有意义的问题。本文通过SLCE 序列的自相关函数值研究了其2-adic 复杂度，给出了SLCE 序列可以达到最大2-adic 复杂度的一个充分条件，并举例证明确实存在大量能达到条件的SLCE 序列，这些SLCE 序列能够抵抗有理逼近攻击，结合SLCE 序列高线性复杂度[3-6]可知，这些SLCE 序列是密码学意义上的好的伪随机序列。