用蝴蝶结法测试毛织物弯曲性

余 芳， 刘成霞

( 1. 绍兴文理学院 元培学院， 浙江 绍兴 312000； 2. 浙江理工大学 服装学院, 浙江 杭州 310018)

织物弯曲性能，也称硬挺度(越易弯曲的织物，其硬挺度越小，即越柔软)，是影响服装风格[1]和美观性的重要指标[2]，因此，众多学者们[3]对其进行了大量研究[4]。如水滴法[5]测试织物弯曲性能的原理是：柔软的面料易形成细长的水滴，硬挺的面料易形成丰满的水滴，根据水滴形状可预测织物的硬挺度。利用凹陷法[6]测试织物多方向硬挺度的优点是：可弥补目前每种方法只能测试织物某一个方向弯曲性能的不足。针对目前织物的弯曲性能和悬垂性是分开独立测试的现状，刘成霞等[7]提出了一种可同时测试这2种性能的方法，节省了测试成本。除测试方法外，还有学者研究了如何利用不同的算法预测织物的弯曲性能，如利用织物实际弯曲形态，经过公式推导得到弯曲性能[8]，以及如何利用BP神经网络预测织物斜向弯曲性能[9]。

综上，目前用得最多，同时也是国家标准规定的测试织物弯曲性能的方法是斜面悬臂梁法[10]，但斜面悬臂梁法存在的问题是：1块试样只能得到 1个测试结果，要得到多个测试结果需要多块试样，尤其对于高档面料，难免造成一定的材料浪费，同时也耗费较多的时间裁剪面料。众所周知，纺织面料是易变形的柔性体，测试结果存在偶然性和不确定性，为减少测试误差，需要进行多次测量，例如同样的织物试样通常要裁剪5块，做5次相同的测试，对结果求平均值。这一现象对于高档面料来说是一种浪费，因此，如果能利用1块织物试样就可得到多组测试结果，无疑可节约测试成本。

此外，由于弯曲性能是织物柔软变形能力的体现，对服装的外观挺括性有直接影响，而且作为对挺括性有较高要求的高档西装来说，其主要材料是毛织物，因此，本文的实验对象为含毛类机织物，以期通过研究，探索出一种既简便又节约用料的测试方法，可快速获得毛织物的弯曲性能，为高档西装制作前的选材提供参考。

1 实验部分

1.1 试样的选取

本文研究对象为18种含毛机织物，由江苏阳光集团提供，详细规格见表1。表中织物的经纬纱原料相同。

表1 织物规格参数Tab.1 Fabric specification parameters

1.2 斜面法测试织物弯曲性能

参照GB/T18318—2001《纺织品 织物弯曲长度的测定》，将表1中的18块织物按照经向、45°和纬向3个角度进行试样裁剪，每个方向裁剪5块试样。测试仪器为YG(B)022D型全自动织物硬挺度测试仪，参数设置如下：检测角度为41.5°，推出速度为 4 mm/s，分正面朝上和反面朝上进行弯曲性能测试，每种织物的5块试样正反面共测得10个抗弯刚度B(μN·m)值，对其取平均值作为该角度下的抗弯刚度。本文中所有实验均在标准大气状态下进行。

1.3 蝴蝶结法测试弯曲性能

1.3.1 测试原理

蝴蝶结法测试织物弯曲性能的原理是将长方形毛织物试样的2条长边对齐，并在长度方向的中心位置用夹子夹住，如图1所示。图中显示用夹子将毛织物的中间部分固定以后，其2条宽边会由于织物弯曲性能的不同而打开成不同的角度，同时宽度和面积也有所不同。从正面看上去，夹子固定后的织物形状恰似一个蝴蝶结，故将其命名为蝴蝶结法。

1.3.2 测试前的准备

1)实验用具及材料：数码相机、实验台、针形夹、固定试样用的白色聚苯乙烯板、若干针形夹。

2)实验环境及条件：标准大气环境，光照均匀且充足的室内。

图1 蝴蝶结法测试原理Fig.1 Testing principle of bowknot method.(a) Front of 1# fabric; (b) Profile of 1# fabric;(c) Front of 4# fabric; (d) Profile of 4# fabric

3)试样：将18种织物熨平后，分别按照经向、与经纱成 45°和纬向 3 种丝缕方向，将其剪为长 8 cm、宽4 cm(经过多次实验，此规格的织物测试结果较准确)的长方形(标上经向丝缕记号)，每种织物准备3块试样。

1.3.3 实验流程

1)将裁剪好的织物试样在标准大气条件下放置 24 h，标出2条宽边的中点，连接2个中点，即画出平行于2条长边的平分线。

2)将长方形试样的2条长边对齐，且用针形夹固定在平分线的中点处，并使针形夹的方向与试样宽边平行。此时，试样由于受到外力的作用而呈现蝴蝶结的形态。

3)将蝴蝶结试样固定在白色聚苯乙烯板上，且在试样正前方固定位置处放置一个黑色边长为 1 cm的小正方形，作为参照物，用于计算蝴蝶结法提取的图像参数所对应的实际尺寸。

4)检测装置如图2所示。在聚苯乙烯板的正上方放置相机架，数码相机置于相机架上，用于从正上方对试样拍照，且在试样的宽边方向上也放置一架数码相机，用于固定位置拍摄试样的侧面形态。

图2 检测装置Fig.2 Testing instrument

5)在试样的蝴蝶结形态稳定 1 min 后，用调好参数的数码相机对其进行拍照，并记录织物编号及所测织物丝缕方向(经向、45°、纬向)。

1.3.4 表征织物弯曲性能的指标

将以上所拍照片导入AutoCAD图像处理软件，利用此软件的查询不规则图形距离、面积和角度的功能进行弯曲特征的提取[5]，如图3所示。引入蝴蝶结面积A、宽度W、高度H及夹角θ作为评价织物弯曲性能的指标。

图3 蝴蝶结法提取的弯曲性能指标Fig.3 Extraction of parameters in bowknot method.(a) Front; (b) Profile

1) 面积A:从正面拍摄的照片上，蝴蝶结试样的两翼所形成的面积(见图3(a))。

2) 宽度W: 用针形夹固定后，长方形试样的宽边弯曲后所形成投影的直线距离。

3) 高度H:在侧面照片上，蝴蝶结试样的2个端点与弯曲试样最低点的垂直高度。由图3(b)可知, 高度H为圆圈所示的织物端点与最凹陷点的垂直距离，并非图中三角形所示的针形夹固定的织物位置(针形夹固定的织物位置与最凹陷点的垂直距离为织物宽度4 cm的一半，即2 cm)。如图1(c)和(d)所示，柔软性不同的面料形成的高度H亦有所不同，硬挺的面料形成的H较大，柔软的面料易受织物重力的吸引而使织物的端点靠近桌面，从而导致H较小。

4) 夹角θ：在正面照片上，以针形夹为顶点，以蝴蝶结的2条布边所做的切线为2条边，所形成的夹角。

由于每块试样形成的蝴蝶结都有两翼，所以可提取的参数均有2组，这在一定程度上比斜面法更具有优势，将2组参数求取平均值作为该块试样的测试结果，再将同一织物3块试样的测试值求平均，可得到每种织物的最终结果。测试结果如表2 所示。

2 结果与讨论

2.1 不同方法各指标间的相关性

将表2中用悬臂梁法与蝴蝶结法所测指标通过相关分析，得到Pearson相关系数如表3所示。其中参与相关分析的样本量为54个(18块试样，每个试样经向、纬向、45°方向共3组数据)。

从表3可看出：蝴蝶结法中的4个指标，即蝴蝶结面积、宽度、高度和角度，与斜面悬臂梁法中的抗弯刚度之间具有较好的相关性，其中与抗弯刚度呈正相关的是蝴蝶结面积、宽度和角度，呈负相关的是蝴蝶结高度。可以解释为：抗弯刚度越大的面料，即越硬挺的面料，形成的蝴蝶结面积、宽度和角度越大，高度越小。其原因可能是越硬挺的面料，在受到夹子固定的外力作用下，越不易屈服，即抵抗外力的能力越强，越易保持原有的平整状态，因而面积、宽度和角度都较大(见图1(a))；而柔软的面料则易在外力作用下改变原有的形状，因此，形成的蝴蝶结比较狭长；从侧面看，蝴蝶结的宽边弯曲较明显，因而高度较大，如图1(d)所示。

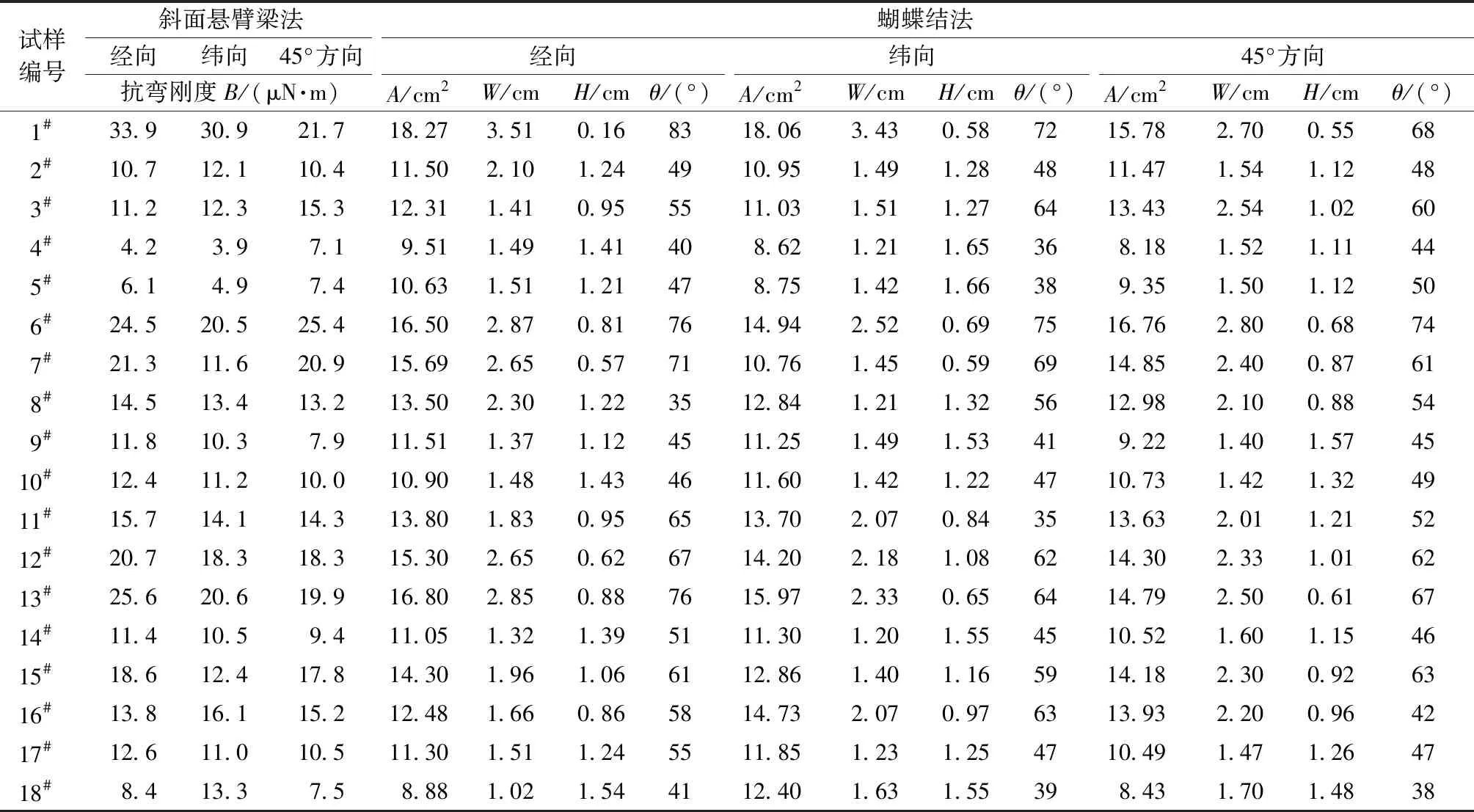
表2 织物弯曲性能测试结果Tab.2 Results of fabrics bending performance

表3 织物各弯曲性能指标间的相关系数 Tab.3 Correlation coefficients of bending performance

注：**表示 在0.01 水平(双侧)上显著相关。

2.2 蝴蝶结法的弯曲指标与抗弯刚度关系

图4示出经、纬、45°这3个方向共54个样本，斜面法所测的抗弯刚度B与蝴蝶结法所测的蝴蝶结面积A之间的关系。可知，抗弯刚度与蝴蝶结面积呈较好的正相关关系，二者的具体关系式为Y=0.172 91X12-2.071X1+11.826，R2=0.949 2, 其中X1为蝴蝶结面积A(cm2)，Y为抗弯刚度B(μN·m)。即抗弯刚度越大的织物，用本文提出的方法进行测试时，蝴蝶结面积越大。可以解释为越硬挺的面料，在外力作用下越不易屈服，越易保持原有状态，因而蝴蝶结宽度越大；相反地，柔软的面积则越易被夹子固定这一外力改变原来的形状，宽度越小。这一原理有点类似质量大的物体其惯性也越大的物理现象。另外，可根据抗弯刚度与蝴蝶结面积之间的二次多项式，由蝴蝶结面积的大小推算和预测织物的抗弯刚度；当无需知道精确的抗弯刚度数值时，则可根据蝴蝶结面积的大小，来快速得到毛织物的弯曲性能好坏。

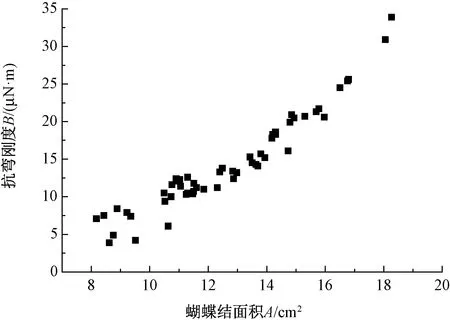
图4 抗弯刚度与蝴蝶结面积之间的关系Fig.4 Relationship between bending rigidity and bowknot area

图4还显示，当面料的抗弯刚度较小时，曲线的拟合效果较差，这可能是因为柔性较大的面料，表现出来的性能更加不稳定，即离散性较大。而较为硬挺的面料则表现为较好的刚性，即稳定性更佳，因此，其规律也更易通过实验测试获得。

由表3可知，蝴蝶结面积与抗弯刚度的相关性最好，其次是蝴蝶结宽度、角度和高度，因此，接下来进一步探究蝴蝶结宽度与抗弯刚度之间的关系。

图5示出54个样本用斜面法所测的抗弯刚度B与用新方法所测的蝴蝶结宽度W之间的关系。二者具体的关系式为Y=2.671X22-1.729 6X2+7.079 2，R2=0.838 9，其中X2为蝴蝶结宽度(cm)，Y为抗弯刚度B(μN·m)。即抗弯刚度越大的织物，用本文提出的方法进行测试时，蝴蝶结宽度越大。其原理与蝴蝶结面积类似，在此不再赘述。

图5 抗弯刚度与蝴蝶结宽度之间的关系Fig.5 Relationship between bowknot width and bending rigidity

通过对比图4、5的相关系数R可以发现，蝴蝶结面积与抗弯刚度的相关性大于蝴蝶结宽度。其原因可能是，相比宽度这个单一维度的指标来说，面积更能综合表征织物性能，涵盖了宽度、长度、角度等多个维度，因而更能体现毛织物在外力作用下的变形能力。另外，尽管蝴蝶结宽度与抗弯刚度的相关性比蝴蝶结面积稍差，但其测量更为简单(可用直尺直接量得)，因此，在精度要求不是太高的情况下，比蝴蝶结面积(需要用图像处理软件获得，无法直接测量)这一指标的获取更加快速方便，在实际应用时更具优势。

与斜面法相比，本文方法还具有以下优势：由于所形成的蝴蝶结有两翼，所以可以用一块试样得到2组测试结果，而斜面法每次只能测试1块试样，得到1个测试结果，所以本文方法效率更高，也更加节约实验材料；同时操作很简单，所需用品极为常见，可以快速估算织物是否容易弯曲，如果想得到较为精确的抗弯刚度，也可通过简单的计算获得。

3 结束语

本文以18种含毛织物为研究对象，用斜面悬臂梁法分别测试其抗弯刚度，然后用自行设计的蝴蝶结法测试其弯曲性能，并用图像处理软件求取蝴蝶结面积、宽度、高度和角度，并以此作为评价指标，经过研究得出以下结论。

1)蝴蝶结法中的4个指标(蝴蝶结面积、宽度、角度和高度)与抗弯刚度都具有较好的相关性。且抗弯刚度越大的面料，形成的蝴蝶结面积、宽度和角度越大，高度越小。

2)抗弯刚度与蝴蝶结面积呈较好的正相关关系，二者的具体关系式为Y=0.172 91X12-2.071X1+11.826，R2=0.949 2, 其中X1为蝴蝶结面积，Y为抗弯刚度。可以根据此二次多项式，由蝴蝶结面积推算和预测毛织物的抗弯刚度。

3)当对织物弯曲性能的精度要求不是很高的情况下，可用直尺直接测量蝴蝶结宽度，来快速比较不同羊毛织物弯曲性能的差异。

本文提出的蝴蝶结法既可较为精确地推算和预测毛织物的抗弯刚度，又可快速比较不同羊毛面料弯曲性能的差异，操作简便，所需材料也极易获得。此外，利用1块试样就可得到2组测试结果，在节约测试原料的同时，也能节省裁剪面料的时间，降低面料，尤其是高档面料的测试成本。

FZXB