基于贝叶斯网络的地铁牵引变电所可靠性分析

何江海，裴卫卫，闫雅斌，鲁晓珊，邢宗义

（1. 广州地铁集团有限公司，广州 510308；2.南京理工大学 自动化学院，南京 210094）

地铁因其运输量大、节能环保、快速安全和准时性好等优点，成为城市轨道交通发展的重要方向，是目前缓解大中型城市交通拥挤的主要方式[1]。城市地铁线路的快速发展极大地方便了民众的日常出行，与此同时，地铁牵引供电系统的安全可靠运行也面临着新的挑战。

目前，国内外学者对牵引供电系统的可靠性研究已经取得诸多进展，其主要研究对象集中在铁路的交流牵引供电系统[2]；而对于地铁牵引供电系统可靠性研究方面，因其系统主接线形式、运行方式和供电方式等均与铁路牵引供电系统存在差异，因此，也有许多学者对其展开深入研究。其中，李想结合可靠性框图法和故障树法对地铁接触网展开了综合分析[3]；曾德容通过故障模式与影响分析法和故障树法相结合，对地铁牵引供电系统展开可靠性研究，提出了系统故障数据的预测方法，进一步丰富了该领域的可靠性研究[4]。曹景雷采用GO法分别构建了地铁牵引变电所和架空接触网的可靠性模型，并对其中的供电网络和一段供电区间进行了可靠性计算，采用层次分析法对地铁接触网的主要设备展开可靠性分配[5]。徐浩结合故障树和贝叶斯网络各自在建模和计算过程中的优势，简化了基于故障树分析法的计算复杂度，对地铁牵引变电所顶事件的失效概率及各节点的后验概率进行定量计算。但是，以上研究没有考虑牵引变电所不同的运行方式和故障模式对可靠性模型结构造成的影响[6]。

本文基于贝叶斯网络，通过GeNIE仿真软件计算地铁牵引变电所（简称：变电所）可靠性模型顶事件的故障率，并采用联合树推理算法对变电所的网络模型展开推理计算，得到各个节点的后验概率排序，定量地识别出变电所的薄弱环节；同时，基于动态贝叶斯网络建立变电所的可靠性模型，并在时间维度上对该模型展开计算，得到了变电所随时间变化的故障率曲线及后验概率排序等，进而得到影响变电所稳态可靠性的主要因素，为变电所监测与设备维护提供理论支撑。

1 贝叶斯网络

1.1 贝叶斯网络的基本原理

贝叶斯网络采用有向图的方式表述系统变量间的概率关系，解决系统各元件因条件相关性而引起的不确定性问题[7]。在实际应用中，贝叶斯网络可以利用概率论和图论方法系统地描述随机变量之间的关系，进而从不完整的或者不精准的信息中做出推理和判断；同时，贝叶斯网络还可以方便地进行概率推理，即计算各事件发生时系统各元件的后验概率情况。

1.1.1 贝叶斯网络概率论基础

概率论是贝叶斯网络理论发展的基础，在利用贝叶斯网络理论进行计算推理时常用的概率论知识包括：条件概率、贝叶斯公式、先验概率、后验概率以及条件独立等[8]。

设事件集合E，B为事件集合的样本数据，且B={Bi,B2, …,Bn}是一个相互独立的事件组，P(Bi)＞0，A是E中的任意事件，则贝叶斯公式如式（1）所示。

式（1）中，P(Bi)表示先验概率，一般由专家分析判断或者根据现有历史统计数据计算得到，是网络中的初始概率值；P(Bi|A)表示后验概率，可以由元件先验概率经贝叶斯公式修正以后得到；P(A/Bi)表示条件概率，表示在事件Bi发生的条件下，事件A也发生的条件概率。

1.1.2 贝叶斯网络图形描述

贝叶斯网络图形主要是由节点和有向边组成的有向无环图，其中，节点包括根节点、叶节点以及中间节点3种类型，分别代表系统中不同的随机变量，而连接各节点的有向边则表示节点间的逻辑关系；同时，父节点与子节点之间的逻辑关系可以用条件概率表表示。

图1是一个贝叶斯网络的图形表示，包含4个节点和4条有向边。图中，P(C=1)=0.4，表示节点C的先验概率，而节点B、D、S标注的是条件概率表。

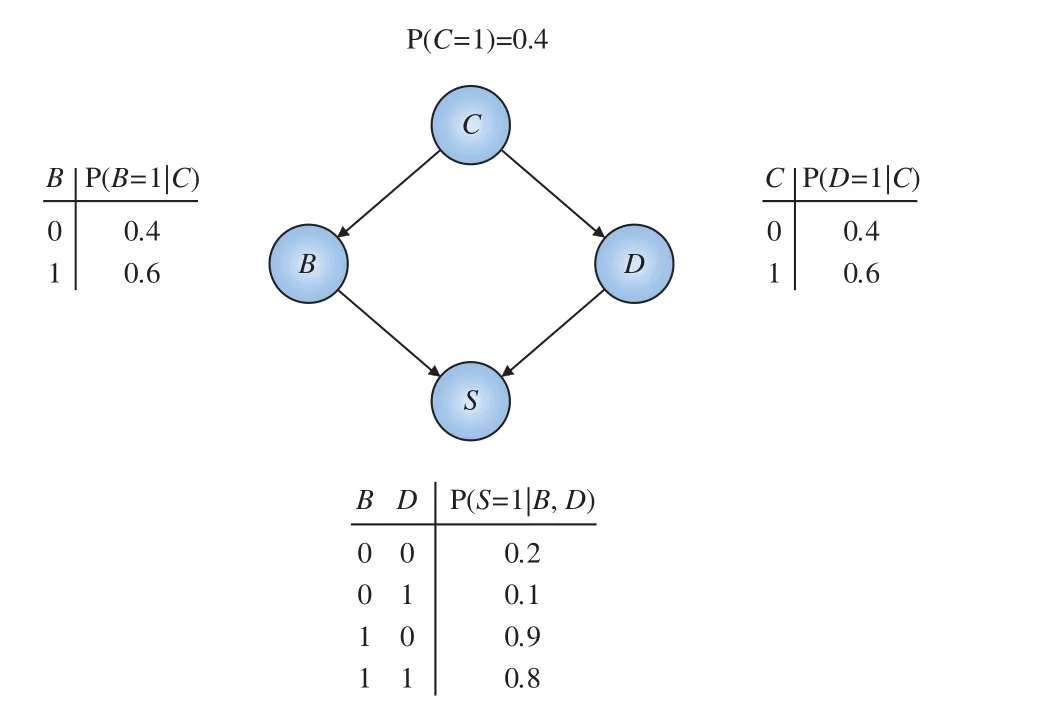
图1 贝叶斯网络的图形表示

1.1.3 贝叶斯网络推理算法

贝叶斯网络推理是根据节点的先验概率和条件概率表计算某一事件发生的概率。在可靠性分析的理论应用中，贝叶斯网络的优势在于其可以进行双向推理，即可以利用父节点和子节点之间的互相关系，由上到下由故障原因得到推断结果，也称因果分析；也可以自下而上推理得到系统故障时各节点的后验概率，从而推测出系统故障的原因，该方法也称致因推理或诊断推理。贝叶斯网络推理算法包括精确推理算法和近似推理算法两类，其中，精确推理算法用于系统结构较小的贝叶斯网络，主要包括组合优化方法、全局联合推理算法、团树传播算法等。近似推理算法用于网络结构中节点数量较多的大型贝叶斯网络，以此来解决节点数量过多引发的计算量过大问题，主要包括基于搜索的方法、随机模拟方法等。

在贝叶斯网络推理过程中，选择合理的推理算法可以提高推理速度和结果精度。其中，团树传播算法的推理结果精确、计算效率高、具有较强的灵活性和适应性，是目前常用的一种精确推理算法。

1.2 动态贝叶斯网络基本原理

动态贝叶斯网络是在静态贝叶斯网络的基础上对引入时间问题的拓展，在继承了贝叶斯网络分析推理优势的同时，将静态的网络结构拓展到时间维度，形成了可以解决时序问题的网络模型[9]。

1.2.1 动态贝叶斯网络表示

在用动态贝叶斯网络描述动态系统的随机模型时，需要得到系统随机变量X[1]，……，X[n]的联合概率分布。因此，在研究复杂动态系统模型时，需要基于平稳假设和马尔可夫假设两个约束条件来简化处理，则动态贝叶斯网络描述的随机过程联合概率分布可以由静态的初始网络和转移网络两部分组成[10]。

初始网络B0表示事件在初始状态X[0]下的联合概率分布。转移网络B→表示事件在X[t-1]，X[t]，t=1, 2, …,n下的转移概率分布，记作P(X[t]|X[t-1])。则给定动态贝叶斯网络模型B*(B0,B→)的初始网络和转移网络，其随机变量X[1], …,X[n]的联合概率分布可以表示为：

由式（2）可知，动态贝叶斯网络模型描述了系统在动态随机过程中时间轨迹上的概率分布情况，图2是一个简单动态贝叶斯网络的图形表示。

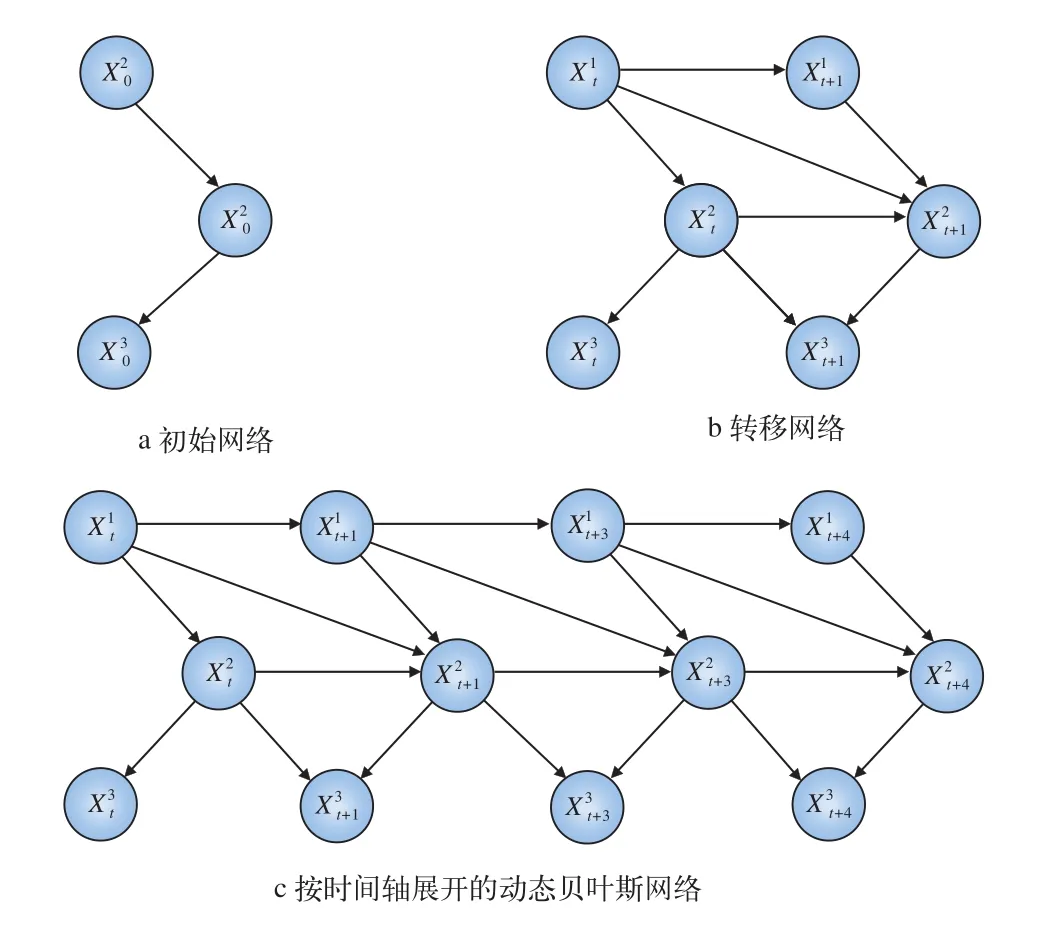
图2 动态贝叶斯网络示意图

1.2.2 动态贝叶斯网络推理算法

理论上，动态贝叶斯网络推理可以通过不断复制时间片的方式展开，利用静态贝叶斯网络对其容纳的所有观察序列进行推理。然而，如果当动态贝叶斯网络所要观察的时间比较长时，通过不断复制时间片展开的动态贝叶斯网络结构在计算时需要消耗更多的存储空间；此外，随着新的观察序列加入，动态贝叶斯网络只是简单地重复上述运算过程，每次观察序列的更新也需要较长的运算时间，所以，这类方法计算复杂度较高，并且极大地浪费系统资源。国内外学者通过对动态贝叶斯网络特殊结构的处理设计了一些优化算法，其中，代表性算法包括：（1）动态精确推理算法，如1.5片联合树推理算法、边界（F）推理算法等；（2）动态近似推理算法，如BK推理算法、FF推理算法等。本文采用目前比较主流的1.5片联合树算法对变电所的稳态可靠性指标进行推理。

2 地铁牵引变电所可靠性建模

在可靠性工程中，故障树分析法是可靠性指标计算的常用方法，基于基本事件仅工作在正常和故障两种状态的假设，且通常所描述的事件之间有明确的逻辑关系。但是，对于多态系统和逻辑关系不明确的事件，该方法的应用就有一些局限。考虑到随着变电所节点数量的增加，故障树分析方法中最小路（割）集不交化算法比较复杂且计算量非常大，对于大型复杂网络，一般只能求解近似值。贝叶斯网络独有的双向推理既能够对顶事件进行预测分析，又能够方便地进行反向诊断推理，定量地计算出各单元在变电所中的重要程度，进而避免了故障树分析法在寻找变电所最小（路）割集时的不交化过程，极大地提升了变电所可靠性分析的计算速度。因此，采用贝叶斯网络建立变电所可靠性模型，能够精确、快速地得到变电所的可靠性指标，同时，在考虑维修因素的情况下，建立变电所在时间维度上的动态贝叶斯网模型，进一步补充对变电所稳态可靠性的评价。

2.1 典型地铁牵引变电所主接线

在对变电所进行可靠性研究时，既要考虑其结构组成以及运行方式，还需要充分了解变电所各元件可靠性模型及其故障形式的特性。历史统计数据表明，对于不同类型的设备，其故障率的分布函数也有所不同，如果在构建变电所整个寿命周期的可靠性模型时分别采用不同的故障率分布函数，将会增加可靠性建模及分析的复杂度。综合考虑到电力系统主要设备的故障率往往较低，而通过统计方法得到的可靠性参数误差对变电所可靠性的影响可能会更大，本文根据变电所计算精度和复杂度的要求，以及某线路的实际情况，在计算过程中假设所有元件均处于寿命中期的偶然故障区，即失效率为常数，变电所元件的可靠度函数服从指数分布。

通常，在研究电力系统主要设备的可靠性时，假设这些为可修复元件，即某元件一旦发生故障就退出运行，待检修完成后再恢复到正常工作状态。同时，在计算过程中一般不考虑计划检修，而假设这些元件具有两种状态：正常工作状态及故障状态。

典型地铁牵引变电所的主接线如图3所示，其中，主要设备包括35 kV交流母线、交流断路器、电动隔离开关、手动隔离开关、整流变压器、整流器、直流母线和电流互感器等。同时，根据该牵引变电所的主接线形式，其运行方式可以分为正常运行方式和故障运行方式。

图3 典型地铁牵引变电所主接线图

2.1.1 正常运行方式

正常运行方式下，变电所交流侧为单母线分段形式，两段母线分列运行，进线断路器101、102合闸，分段断路器110分闸；直流侧两套牵引整流机组接在同一段母线上并列运行，越区隔离开关2113、2124处于分闸位置。同时，该变电所通过接触网与相邻的牵引变电所构成双边供电。

2.1.2 故障运行方式

故障运行方式下，当一路引入电源退出运行时，分段断路器110自动合闸，另一路引入电源负责该变电所牵引负荷和动力照明的一、二级负荷；当一套整流机组退出时，另一套整流机组在具备运行条件的情况下可以继续运行，否则该变电所也退出运行；当直流侧单台馈线断路器故障退出时，同一方向的纵向隔离开关合闸进行双边供电；当该变电所（不含终端变电所）故障退出时，由其相邻的两座牵引变电所通过越区隔离开关或者直流母线实行大双边供电，共同负责该区间的牵引负荷；当线路终端牵引变电所故障退出时，只能由相邻的牵引变电所实行单边供电，承担该区间正常供电范围内的牵引负荷。

2.2 典型地铁牵引变电所的可靠性模型

2.2.1 贝叶斯网络模型

贝叶斯网络模型的构建方法：（1）在GeNIE软件中，将图3所示变电所主接线中的基本事件和逻辑关系转换为贝叶斯网络图形中的节点；（2）根据地铁牵引变电所基本事件之间的层次关系使用有向边将贝叶斯网络模型中的节点全部连接起来；（3）设置贝叶斯网络中部分节点的条件概率表，并确定其它节点的先验概率。最终得到典型变电所贝叶斯网络的可靠性模型，如图4所示。其中，各主要设备故障数据，如表1所示；模型中各个节点与基本事件的对应关系，如表2所示。

图4 典型地铁牵引变电所的贝叶斯网络模型

表1 牵引变电所各元件的故障数据

表2 贝叶斯网络模型中各节点的含义

2.2.2 动态贝叶斯网络模型

采用动态贝叶斯网络建立变电所可靠性模型的方法与静态贝叶斯网络类似，主要包括图形节点、有向边、条件概率表、转移概率表，以及先验概率的设置等，不同之处在于动态贝叶斯网络引入了时间因素，在网络模型建立的过程中需要确定同一网络节点当前时间与下一个单位时间之间的条件转移概率。由于动态贝叶斯网络基于平稳假设和马尔可夫假设两个约束条件，则：

同时，动态贝叶斯网络相邻两个时段之间的条件转移概率可以表示为：

其中：1表示节点A失效；0表示节点A正常工作；fA(t)是节点A的失效密度函数；mA(t)是A的维修密度函数。则节点A当前时刻与下一时刻间的转移概率表，如表3所示。

表3 节点A在相邻时刻的转移概率表

对于动态贝叶斯网络，不仅需要对其静态网络进行赋值，还需要对其转移网络进行赋值，若假设变电所各主要设备的修复率和失效率均为常数，即设备寿命函数呈指数分布，则失效密度函数为f(t)=λe-λt、维修密度函数为m(t)=μe-μt。根据表3中转移概率的计算过程，可以获得动态贝叶斯网络中各个节点的条件转移概率表，其中，表4和表5分别是以节点X1为例的条件概率表和相邻时刻的转移概率表。

表4 节点X1在时间片内的条件概率表

表5 节点X1在相邻时刻的转移概率表

根据图4所示的典型变电所贝叶斯网络模型，在GeNIE软件中构建其动态贝叶斯网络，拓扑结构如图5所示。其中，各节点的具体含义与静态贝叶斯网络节点相同。

图5 典型地铁牵引变电所的动态贝叶斯网络模型

3 地铁牵引变电所可靠性分析

3.1 可靠性模型计算

在确定了变电所贝叶斯网络的拓扑结构、节点先验概率、条件概率后，对变电所的可靠性模型进行计算，得到该变电所不能对上行接触网正常供电的概率为0.015 686 644%；若要求变电所的可靠度不低于0.9，为保障变电所的可靠运行，其预防性检修的时间间隔不宜超过671 h。在动态贝叶斯网络中设置节点初始概率和转移概率后，可以得到考虑维修因素时变电所失效率随时间变化情况，如图6所示。

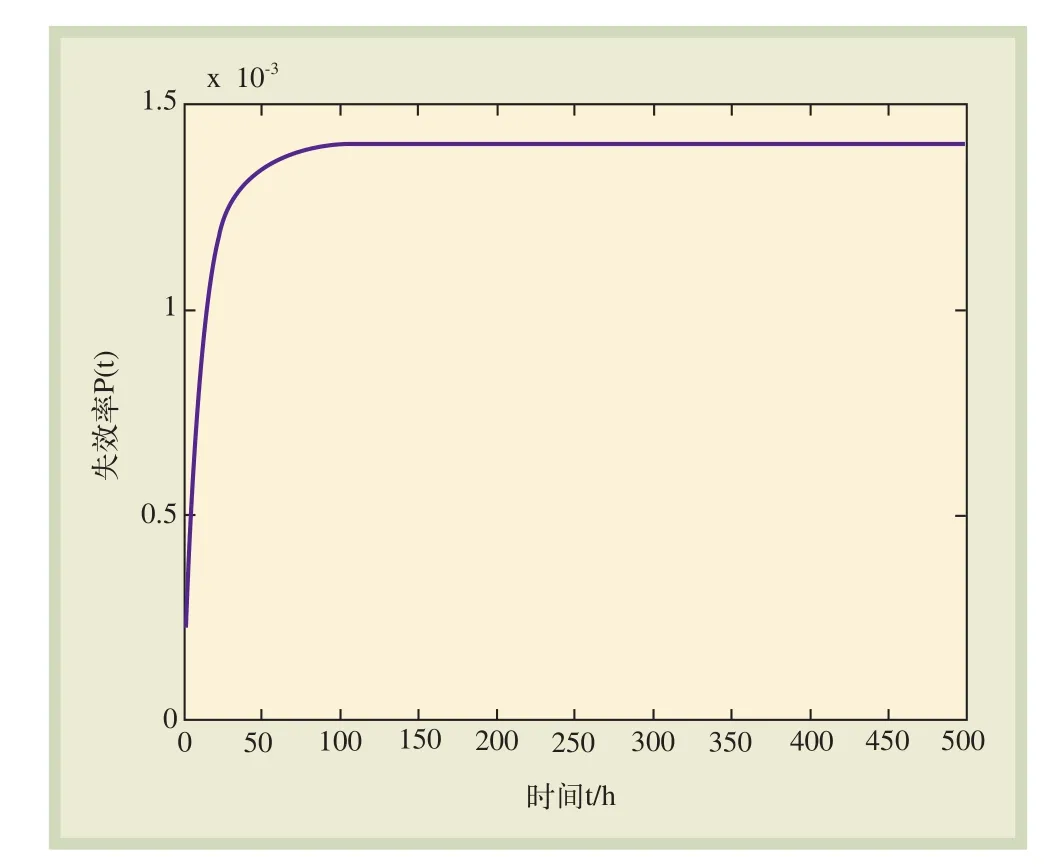
图6 失效率随时间的变化曲线

3.2 故障条件下主要节点后验概率计算

在考虑维修因素时，变电所稳态运行一段时间后可以发现，在运行初期，其失效概率会迅速增长，而随着时间的推移，在180 h后，失效率达到稳态，其稳态失效率约为0.140 355 05%。同时，利用贝叶斯网络的反向推理功能，可以分别计算出变电所故障条件下，各元件在静态贝叶斯网络和动态贝叶斯网络中的后验概率情况，如表6所示。

表6 牵引变电所主要节点的后验概率表

3.3 结果分析

根据表6可知，在静态贝叶斯网络中，直流母线、35 kVⅠ段母线对牵引变电所可靠性的影响比较大，后验概率分别达到了47.30%和21.83%，是变电所可靠性的薄弱环节，上述计算结果与变电所运行中导致变电所失效的直接原因为直流母线或者交流母线断电的实际情况相符；在考虑到维修因素的动态贝叶斯网络中，直流母线、35 kV进线电源、整流变压器等的后验概率排名比较靠前，说明以上节点是系统稳态后，的薄弱环节，在维护保养过程中需要对以上部件加强维护，以提升各单元的可靠性来提升双边供电方式下该供电分区整体的可靠性。

同时，根据表6的对比结果可知，在考虑维修因素后部分节点的后验概率发生较大变化，其中，主要是整流变压器、整流器和35 kV进线电源对变电所可靠性的影响大幅提升，说明在考虑维修因素时，设备的维修率会对节点在变电所中的重要度产生影响，如变压器和整流器等是变电所的关键设备，虽然其故障率较低，导致变电所失效的后验概率较小，但考虑到该设备的修复时间长、修复率低等维修因素时，其对变电所的稳态可靠度影响程度将大幅增大。因此，除了通过降低设备自身的故障率以外，还可以对变电所关键设备的维修策略进行优化，使变电所可以长时间维持在较高的可靠度水平上。

4 结束语

本文采用贝叶斯网络对地铁牵引变电所进行可靠性分析，通过GeNIE仿真软件建立了典型变电所基于贝叶斯网络的可靠性模型，对其发生故障的概率进行计算；利用动态贝叶斯网络对该变电所在时间维度上展开分析，得到变电所故障概率随时间变化的曲线；利用贝叶斯网络的双向推理功能，计算得到变电所在初始状态和稳态下各元件的后验概率排序，找到变电所的薄弱环节。对变电所关键节点的识别、维护，以及网络结构优化具有一定意义。