基于图着色理论的阵列天线校正方法

高卫斌，党锐锐，杨李杰

基于图着色理论的阵列天线校正方法

高卫斌1，党锐锐2，杨李杰2

（1 北京跟踪与通信技术研究所 北京 100094 2 浙江大学海洋电子与智能系统研究所 舟山 316021)

由于受环境变化影响，大规模平面相控阵天线收发通道的幅相一致性会发生偏移，常常需要标校才能保证其正常工作，但目前阵列天线收发通道数量较多，校正过程复杂，而且费时费力。基于图着色理论提出一种阵列天线快速校正方法，将校正时隙分配转化为图论中的着色问题，通过最小化时隙着色提高每个校正时隙的复用率，以降低阵列通道校准次数，达到缩短全阵列校正时间目的。仿真表明，对正六边形、正方形和正三角形平面阵列，分别最多仅需要8个、9个和16个时隙就可完成全阵列校正。

图着色理论；阵列校正;平面相控阵；幅度相位误差

引 言

相控阵天线必须保证各收发通道幅度相位一致，才能得到符合预期的辐射方向图[1-4]。但环境温度和元器件状态变化可引起各通道间幅相不一致，需要进行定期校正才能保证其性能。

目前校正算法有多种，文献[5,6]提出的旋转电场矢量校正REV算法（Rotating element electric field vector）较为经典，将天线相位从0°旋转到360°，测量整个阵列的复合电场强度，获得各通道幅度和相位值。文献[7]提出REV算法总测量次数与阵列通道数和相位旋转分辨率成正比。假设有个通道，每一个通道移相器比特数是，则总测量数为2。如果将总校正时间划分为非重叠的等长时隙，每个天线占用一个时隙，则总测量数也可表示为每通道测量数乘以总时隙数。阵列通道数越多，REV算法测量总数越大，这是大规模阵列天线标校耗时、耗力的主要因素。鉴于此，有研究者一直在研究减少阵列天线校正总测量数的算法，如文献[8,9]提出的Extended-REV算法和REV-H算法。Extended-REV算法同时测量多个通道的信号，通过连续调制相位，利用傅立叶变换来获得每通道幅度和相位相对误差，总测量数至少为7.5+1；REV-H算法根据归一化Hadamard矩阵将天线阵元分成不同组，同一组中所有通道的相位同时旋转，并据此得出所有通道的相对电场，总测量次数为30。上述所有方法旨在减少每个天线阵列通道的总测量数，但对于大型相控阵天线校正来说仍然效率不高。

本文提出了一种基于图着色理论的快速校正方法，通过提高每个校正时隙的复用率，让多个阵列通道在同一校正时隙内完成测量，从而降低总测量数。与REV算法、Extended-REV算法和REV-H算法相比，基于图着色理论的校正算法实现了最少的总测量数，从而大大减少了相控阵天线的校正时间，阵列天线规模越大，效果越明显。仿真结果表明，基于图着色理论的校正算法分别最多只需要8个、9个和16个校正时隙，就可以完成正六边形，正方形和三角形平面阵列的校正。

1 问题描述

平面相控阵列天线结构如图1所示，每阵元接收和发送通道组成一路辐射单元，射频开关控制天线每阵元收、发模式间切换，假设相邻阵元之间存在着互相耦合效应。

根据上图给出如下定义：

一跳邻居阵元：阵元是的一跳邻居，当且仅当和的距离最短时；

二跳邻居阵元：阵元线的二跳邻居，当且仅当是的一跳邻居时；

跳邻居阵元：阵元是的跳邻居，当且仅当是天线的（–1）跳邻居的一跳邻居时。

以图2中平面阵列为例，圆圈表示天线阵元，根据定义，阵元6的一跳邻居是绿色天线2、天线5、天线7和天线10，阵元6的两跳邻居是灰色阵元1、阵元3、阵元8、阵元9、阵元11和阵元14。

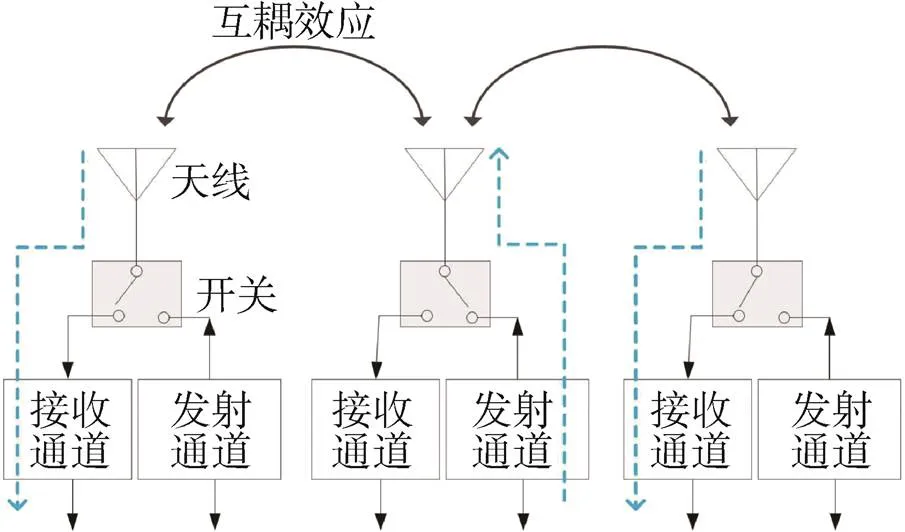
图1 一个典型的相控阵天线架构

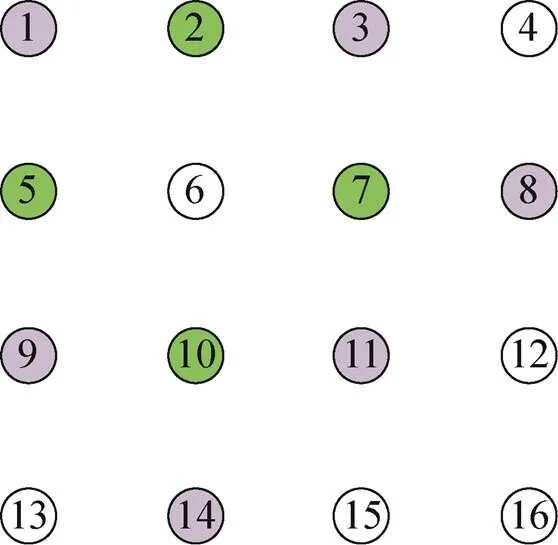
图2 一个包含有16个天线的规则平面阵

1.1 耦合效应

对于规则的平面阵列构型，当天线辐射为全向时，每个天线阵元将向其跳邻居耦合出相同功率的能量，即该阵元和它任一跳邻居之间具有相同互耦系数，耦合能量随着间距增加而衰减，两组阵元同时进行校正，时间距必须保持足够远才能减少互耦干扰。如图3所示，两组阵元同时进行校正，其中第一组阵元包含阵元9和它的一跳邻居阵元，第二组阵元包含阵元13和它的一跳邻居阵元，第1组阵元将受到第2组阵元的互耦干扰，仿真表明，当两组阵元中的发射通道（即图中的9阵元和13阵元）相距四跳或更多跳时，互耦干扰可以忽略不计。

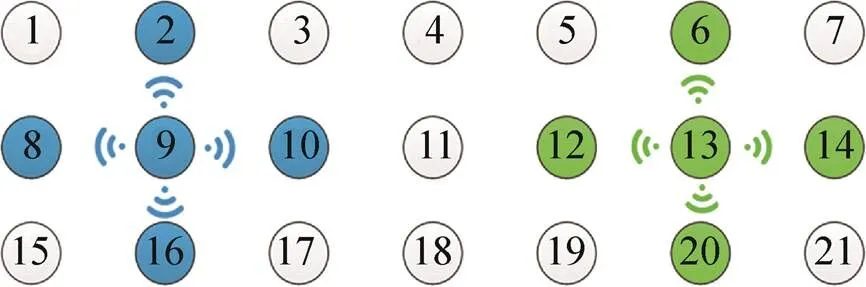
图3 两组阵元同时进行校正示意图

1.2 阵元局部校正

任一阵元和其一跳邻居阵元组成一组，通过执行校正程序得到组内阵元之间的幅相误差，称之为作局部校正。

以图3中阵元组1为例，假设阵元9发射通道工作并发射校正信号，同时所有一跳邻居阵元（即阵元2、阵元8、阵元10和阵元16）接收通道工作并接收阵元9发射的校正信号，基于互耦效应REV算法，可以得到阵元2、阵元8、阵元10和阵元16之间的幅度和相位误差，完成一个阵元局部校正。

这种局部校正会受到其他阵元的辐射影响，如图3。当阵元9及其相邻阵元正在局部校正，而阵元11发射通道工作时，那么，阵元10将会同时接收到来自阵元9和阵元11的辐射信号，其中，来自于阵元11的属于干扰信号会影响阵元10对阵元9的校正信号的接收。因此，传统的校正方法一次仅允许一个阵元发射通道工作，其他阵元都切换到接收模式，仅只有以发射阵元为中心的一小部分邻居阵元能够被校正，每个阵元都重复此项工作才能完成全阵列阵元的校准，大规模相控阵天线往往有上万个阵元，每次完成校准的代价高昂。

1.3 校正时隙分配

为缩短大规模相控阵天线校正时间，可把互耦干扰严重的阵元组用图论中着色方法将其分配到不同的校正时隙当中，在相同校正时隙内执行局部校正时，阵元间不存在相互干扰（或可忽略不计），这样通过恰当时隙分配，阵元校正就可以同时进行，从而节省校正时间。

如果用格点代表天线阵元，用边代表任意两个一跳邻居阵元之间存在的互耦效应，那么就可将相控阵列的校正时隙分配问题转换为图论中的顶点着色问题。优化的目标是得到最小化校正时隙数，也就是最小化顶点着色使用的颜色数。典型的平面相控阵列如图4（a）所示，阵列拓扑如图4（b）所示，当存在失效阵元时，失效阵元会失去与它相邻阵元间的互耦效应，图论中表述为失效顶点和相邻顶点之间不存在边。类似于文献[10-12]提到的时分多址TDMA（Time division multiple access）的规划问题。在阵列校正问题中，将总校正时间划分为若干非重叠的等周期时隙。这些时隙被分配给不同的天线阵元，使得分配在同一个校正时隙内天线阵元组能够在无干扰或干扰尽可能小的条件下同时完成其局部校正。

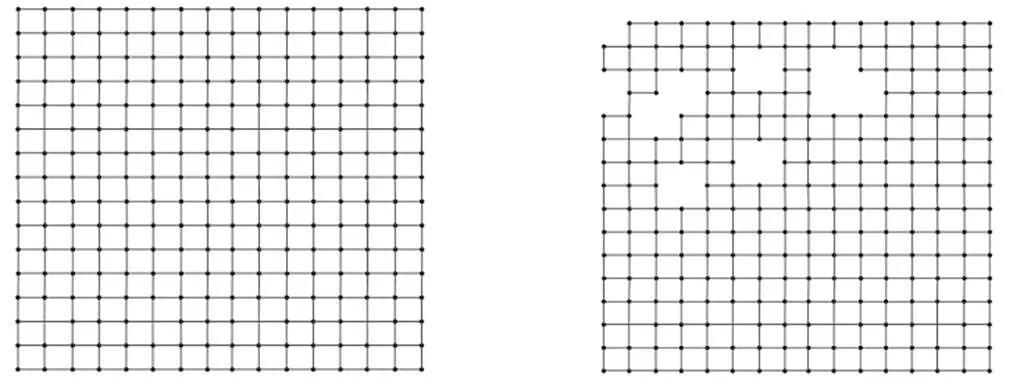
（a）　　　　　　　　　　　　（b）

图着色理论已经大量应用于时间、频率、信道等资源分配问题中[9-11]，这里尝试利用图着色理论来优化相控阵列天线的幅相校正问题。给定一个简单图，=(，)，其中是顶点集合（即阵元集合），是边集合（即相邻阵元之间互耦效应集合）。每个顶点的一跳邻居顶点表示为()={:(,)∈}。为每个阵元分配校正时隙相当于为每个顶点赋予一种颜色，即为提供一种着色策略，即：()→，其中是赋值函数，是颜色集合，的值为正整数，代表不同颜色。任何两个相互干扰的顶点都会被赋予不同颜色。为了提高校正效率，需要最小化颜色数，以便实现最少的校正时隙数。

由于每个天线阵元都由发射通道和接收通道构成，单个天线阵元的校正程序可分为两部分，即接收通道校正和发射通道校正。当接收通道校正时，给定中的任何一个阵元，将设置为发射模式，将的一跳邻居阵元()设置为接收模式。由于的存在，()中的每个阵元都可以接收到发射的校正信号。因此，可以利用局部校正来获得()中各个阵元之间的幅度和相位误差。注意在执行局部校正时，为避免干扰，需要保证的三跳以内（含三跳）邻居阵元不被允许处于发射模式，其他阵元的幅相误差测量依此类推。

发射通道校正类似于接受通道校正，将阵元设置为接收模式，将()中的天线阵元设置为发射模式，接收到的信号是由()中所有阵元发送校正信号的复合信号。随后，利用局部校正方法得到()中的阵元之间的幅相误差。此时，同样需要注意：在执行局部校正方法时，保证的三跳以内邻居阵元不被允许处于接收模式，以防止()中的阵元产生的校正信号对的三跳以内邻居阵元产生干扰。

综上所述，需要解决的校正时隙分配问题可以归纳为如下的图着色优化问题：

目的：最小化；

条件：()≠()，当是的三跳以内邻居阵元，且,∈时。

文献[12]表明，此问题不存在最优解，因此可转而寻找该问题的一个有效解。

2 阵列天线着色校正

恰当的时隙着色是实现大规模天线阵列快速校正的关键。校正时隙着色分为两个阶段：第一阶段，中的每个阵元将获得三跳以内邻居阵元的拓扑信息；第二阶段，所有天线阵元将与三跳内的邻居阵元交换校正时隙分配信息，以实现无干扰校正。

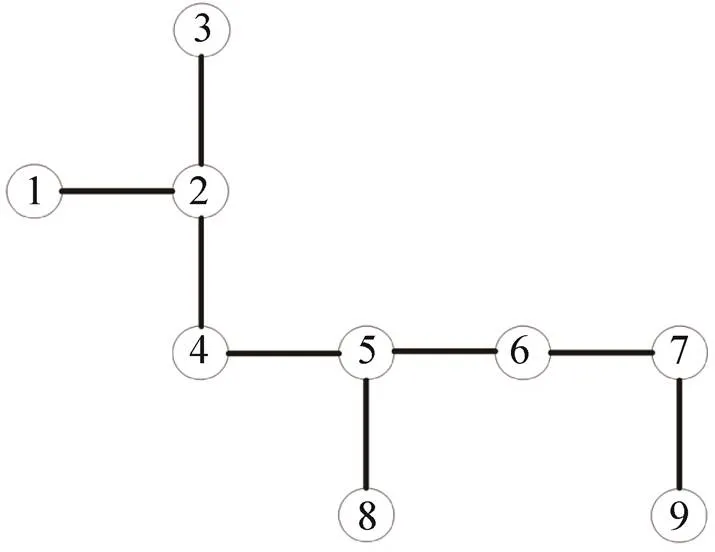
图5 一个包含9个阵元的阵列拓扑图

阶段一：为每个顶点构建一个邻居表，记录三跳以内的邻居阵元信息。如图5所示，一个包含9个阵元的阵列天线拓扑图，圆圈代表不同的阵元，短线代表一跳邻居阵元之间的互相耦合效应。

开始每个顶点不知道三跳以内的邻居阵元编号信息，邻居表是空的，构建邻居表的过程如下：

①阵元1转为发射模式，其他转为接收模式；

②阵元1向外发射自身的编号信息，由于互耦效应，所有阵元都收到该信号，只是距离不同，接收到的信号功率不同，阵元1的一跳邻居阵元（即2）接收到的信号能力要明显高于其他阵元接收到的信号，可以据此设置信号检测阈值，确保一跳邻居阵元接收到的信号强度超过阈值时可被识别，而其他阵元接收到的信号强度低于该阈值而被忽略。通过阈值的设定，阵元1只能将发射的编号信号传递到它的一跳相邻阵元，即阵元2；

③当阵元2接收到该信号时，阵元2将阵元1记录到它的邻居表中，这时阵元2还不知道它的两跳邻居阵元和三跳邻居阵元；

④随后阵元2进入发射模式并广播自身的编号信息，其他阵元变为接收模式。通过相同的阈值设定，该信号被阵元2的一跳邻居阵元（即阵元1、阵元3和阵元4）接收。阵元1、阵元3和阵元4将阵元2添加到它们各自的邻居表里；

⑤在所有阵元都向空间发送过自身编号信息之后，此时，所有阵元都已经初步建立了各自的邻居表，表里包含它们的一跳邻居阵元的编号信息，如表1所示。

随后开始第二轮广播，以获得两跳邻居的信息。每个阵元将自身编号信息及它的一跳邻居阵元信息一同向外广播，据此获取两跳邻居阵元信息。如表2所示，阵元2广播的信息里包含自身编号信息以及其一跳邻居阵元的编号信息，即阵元1、阵元3和阵元4，阵元1接收到该广播信息，知道阵元3和阵元4是阵元2的一跳邻居阵元，就可推断出阵元3和阵元4是阵元1的两跳邻居阵元。

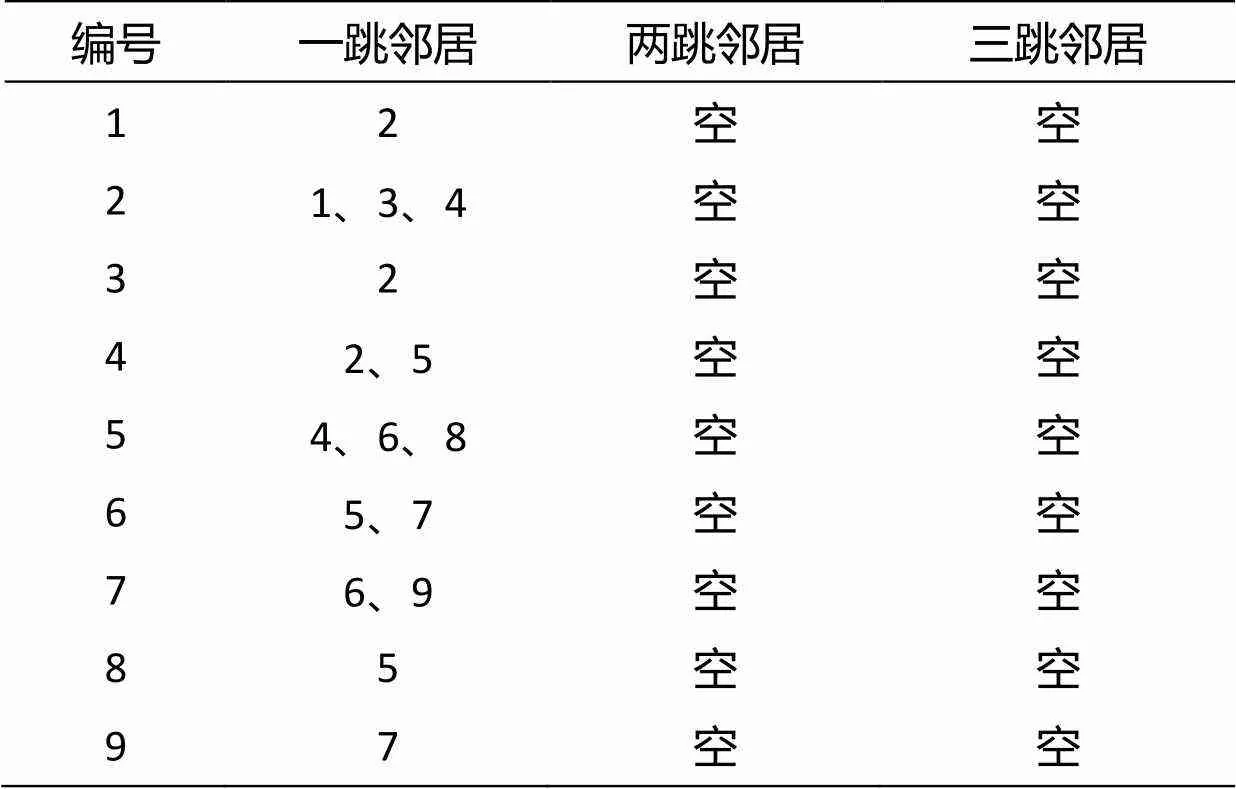
表1 第一轮广播之后所有阵元的邻居表

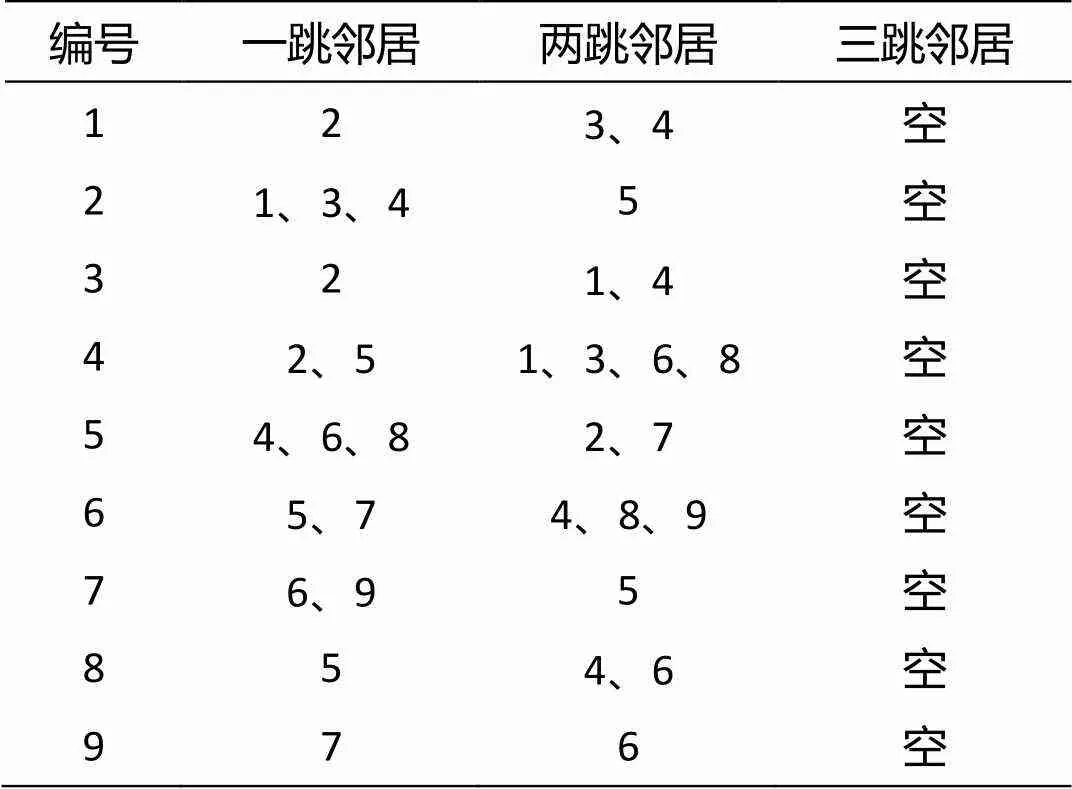
表2 第二轮广播之后所有阵元的邻居表

在第三轮广播中，每个阵元将向外广播自身编号信息以及它一跳、两跳邻居阵元的编号信息。因此，每个阵元都能够得到三跳内邻居阵元的信息，如表3所示。

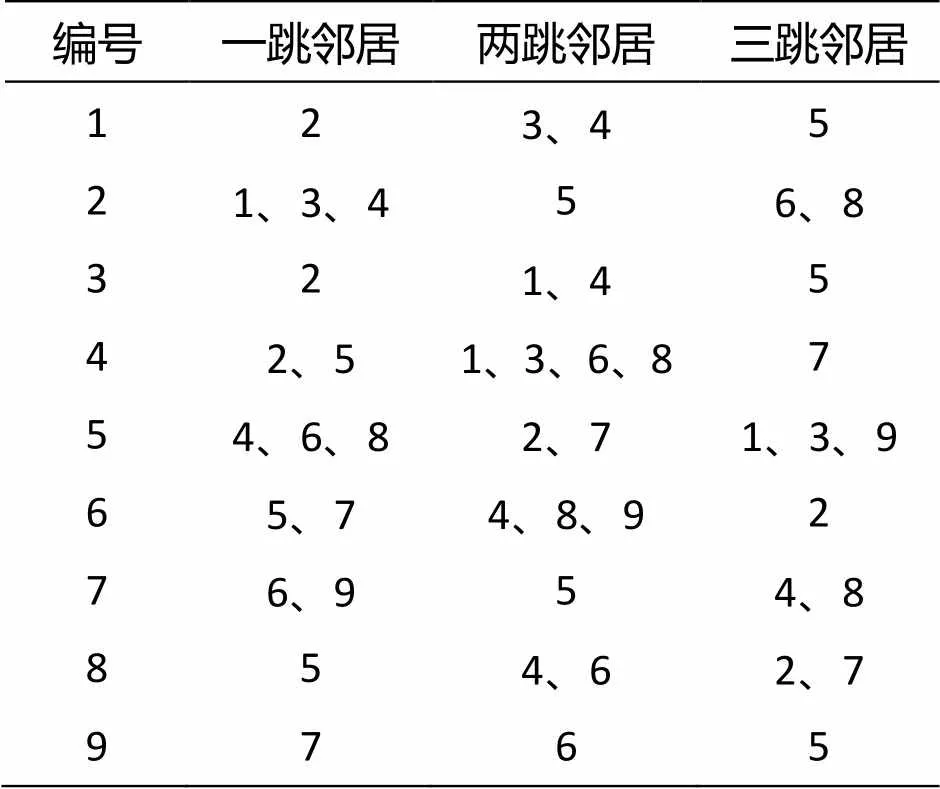
表3 第三轮广播之后所有阵元的邻居表

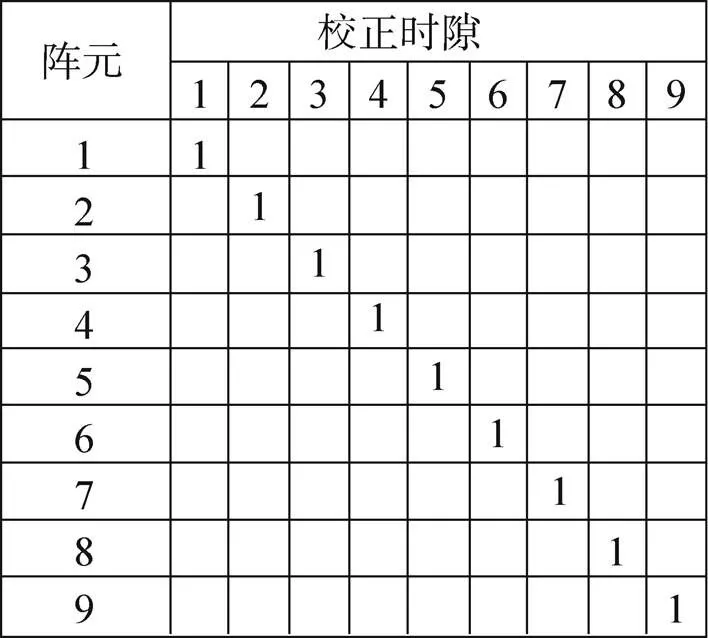
图6 校正时隙分配表初始状态

阶段二：使用时隙分配表来记录每个阵元所分配时隙数。如图6所示，行代表每个阵元，列代表分配的校正时隙数（颜色）。时隙分配表中的每个元素有三种取值：1、0和空白，其定义为：1表示该校正时隙被该行所对应的阵元所占用；空白表示该行所对应的阵元可以使用该校正时隙；0表示该阵元不允许使用该校正时隙，原因是该校正时隙被该阵元的三跳以内邻居阵元所占据。

如图6所示，时隙分配表初始态为第个阵元占据第个校正时隙，第一阶段所有阵元都获得了三跳以内邻居阵元信息，所有阵元也能够据此推断出其三跳以内邻居阵元校正时隙。例如，阵元2可以推断出它的三跳以内邻居阵元所占据的校正时隙数为1个、3个、4个、5个、6个和8个。上述校正时隙无法被阵元2使用，上述校正时隙之外的其他校正时隙都可能被阵元2所使用，此外阵元2还具有阵元1、阵元3、阵元4、阵元5、阵元6和阵元8的邻居阵元的部分信息。特别是阵元2知道时隙1和时隙4对于阵元3是不可用的，因为时隙1和时隙4是阵元2的一跳邻居和阵元3的两跳邻居。而阵元2不知道时隙7和时隙9是否可用于阵元3，因为其不知道阵元7和阵元9是否在阵元3的邻居表中。

推导出的每个阵元校正时隙分配表如图7所示，图7（a）给出了时隙分配表第一次演化结果，所有阵元占据一个校正时隙，同时也知道部分其他校正时隙分配情况；图7（b）给出了阵元1和阵元6同时占据了校正时隙1、校正时隙6被释放、阵元7、阵元8和阵元9不允许占用校正时隙1的结果；图7（c）-图7（f）描述了校正时隙2、时隙3、时隙4、时隙5的分配情况。

获取每个阵元校正时隙分配表后，需要确定无干扰条件下的时隙分配策略。校正时隙1可以分配给多个阵元，比如阵元1和阵元6、或阵元1和阵元7，或阵元1和阵元8，或阵元1和阵元9。

由于有许多种组合方式，可使用以下步骤来确定合适的组合。首先，每个阵元都会广播自己所在行的信息，因此每个阵元都可以获得它的一跳邻居阵元的时隙分配信息；其次，每个阵元都广播自己行信息及其一跳邻居的行信息，此时所有阵元都获得它的两跳以内阵元的行信息；最后，每个阵元再广播自己及两跳以内阵元的行信息。因此每个阵元就得到了它的三跳以内阵元的时隙分配信息。

若阵元8知道时隙1对于阵元2、阵元4和阵元5是不可用的，但该时隙可用于阵元6和阵元7。而阵元8不知道时隙1是否可用于阵元9，因为阵元9不在阵元8的邻居表中。当阵元6、阵元7、阵元8和阵元9同时在时隙1中进行局部校正时，它们之间就会发送严重干扰，必须采用额外的机制来重新分配时隙1，可按照阵元编号大小为每个阵元分配优先级。例如在使用校正时隙1时，阵元6比阵元7、阵元8和阵元9具有更高的优先权，当阵元6占据时隙1时，时隙6被释放并且可供其他阵元使用，当阵元6的校正时隙分配表的信息发生变化时需向它的三跳以内邻居广播该信息，广播后阵元2、阵元4、阵元5、阵元7、阵元8和阵元9就能够清楚地知道时隙1无法使用，而时隙6可以被使用。所有这些变化见图7（b），以灰色高亮显示所有的变化元素。图7（c）到图7（f）表现了时隙2、时隙3、时隙4和时隙5的分配情况，同时总的校正时隙数从9个下降为5个。

图8显示了校正时隙在阵列拓扑图上的分配情况。不同的校正时隙以颜色进行区分，任何三跳以内邻居阵元的校正时隙都是不一样的。图8（a）为9个阵元没有进行校正时隙分配情况，图8（b）～图8（f）校正时隙1～时隙5在各阵元分配情况。

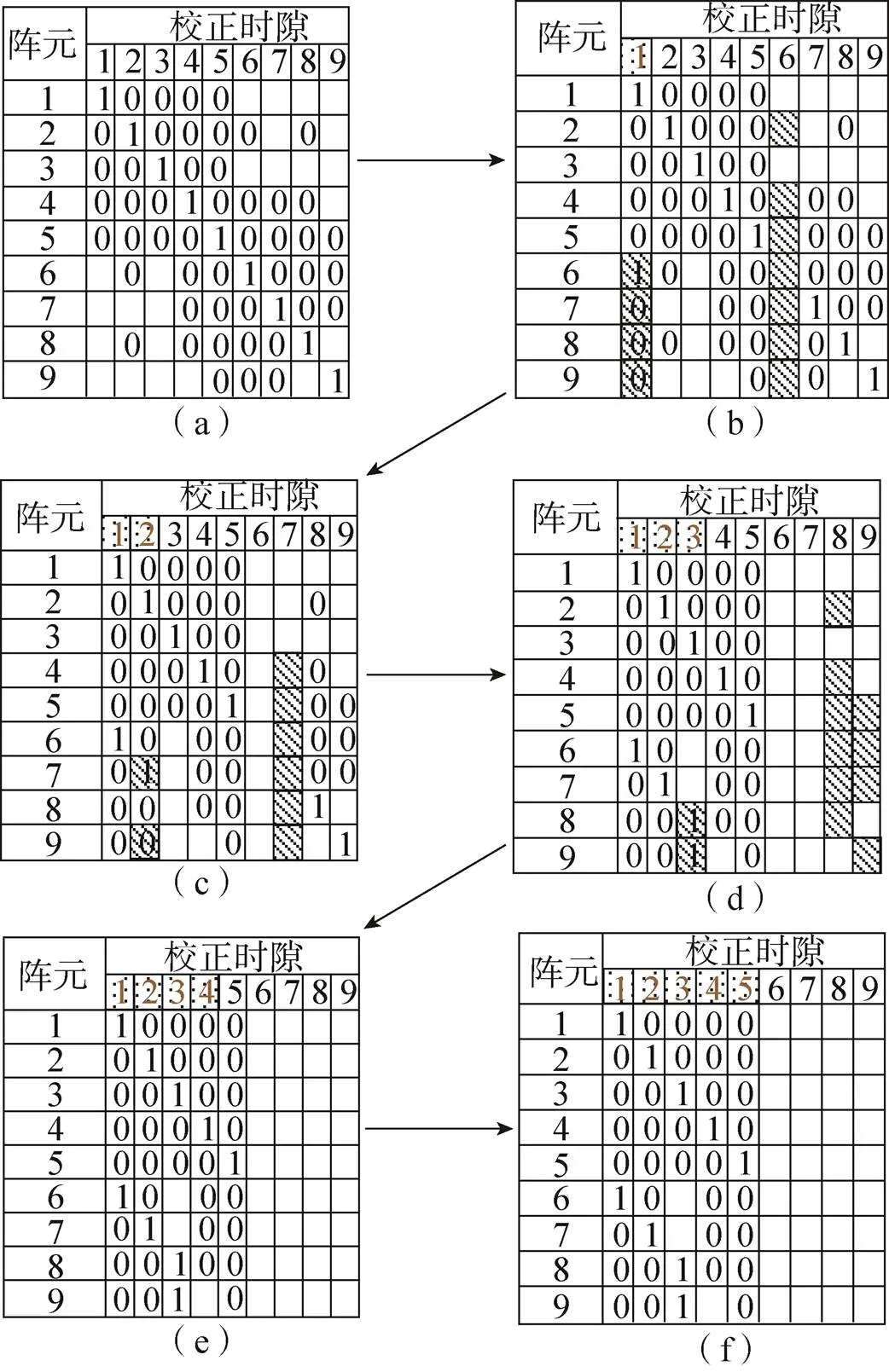
图7 校正时隙分配表演化过程

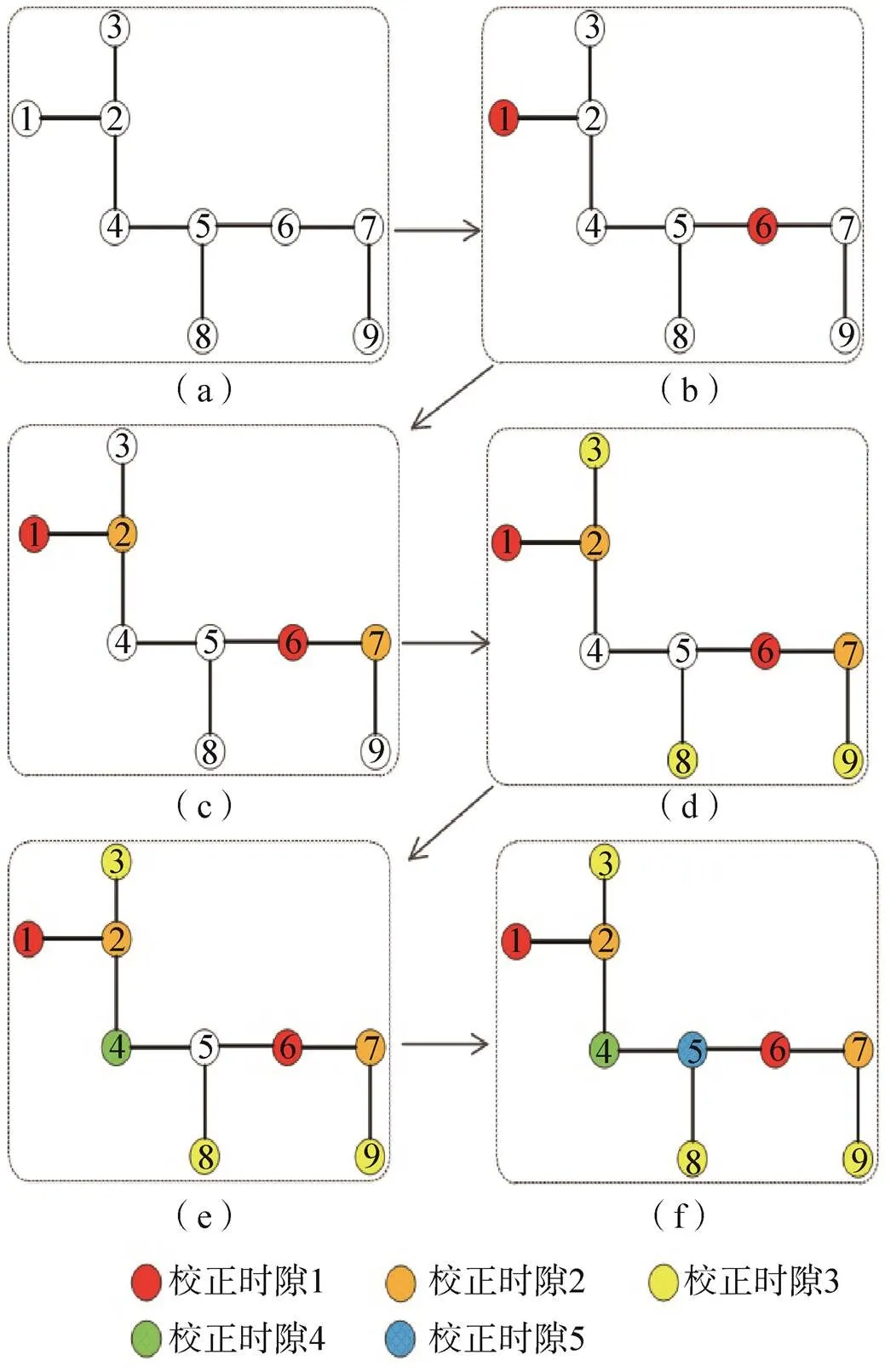
图8 校正时隙各阵元分配拓扑图

3 仿真验证

分别选取正六边形（a）、正四边形（b）和正三角形（c）三种典型平面阵列对提出的着色算法进行仿真，如图9所示。

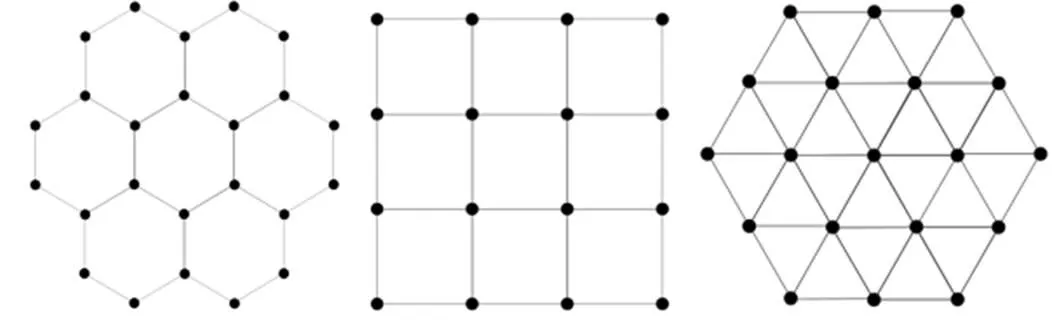
（a）　　　　　　（b）　　　　　　（c）

3.1 互耦效应和天线间距的关系仿真

采用高频结构仿真软件HFSS（High Frequency Structure Simulator）软件评估两圆形贴片阵元之间互耦效应与两阵元间距之间的关系。圆形贴片天线阵元尺寸如图10，设定=51.75mm，=21.11mm，1=0.1mm，2=1.575mm，0=0.65mm。

图11显示了不同阵元间距的互耦效应（21），谐振频率为2.33GHz。表4列出了互耦结果。当从增加到2（=105mm）时，互耦效应衰减18.56dB。当>2时，互耦效应衰减大约13dB/d。仿真结果表明，一跳（=）的接收信号强度比四跳（=4）大46.16dB。

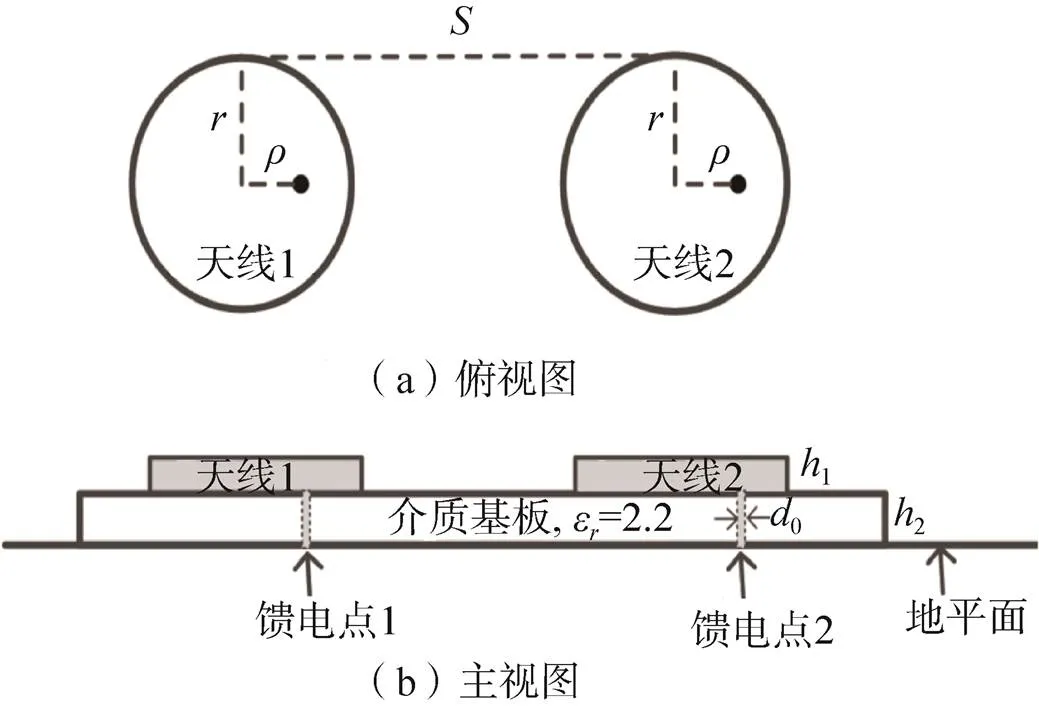
图10 仿真互耦效应的天线阵元布局

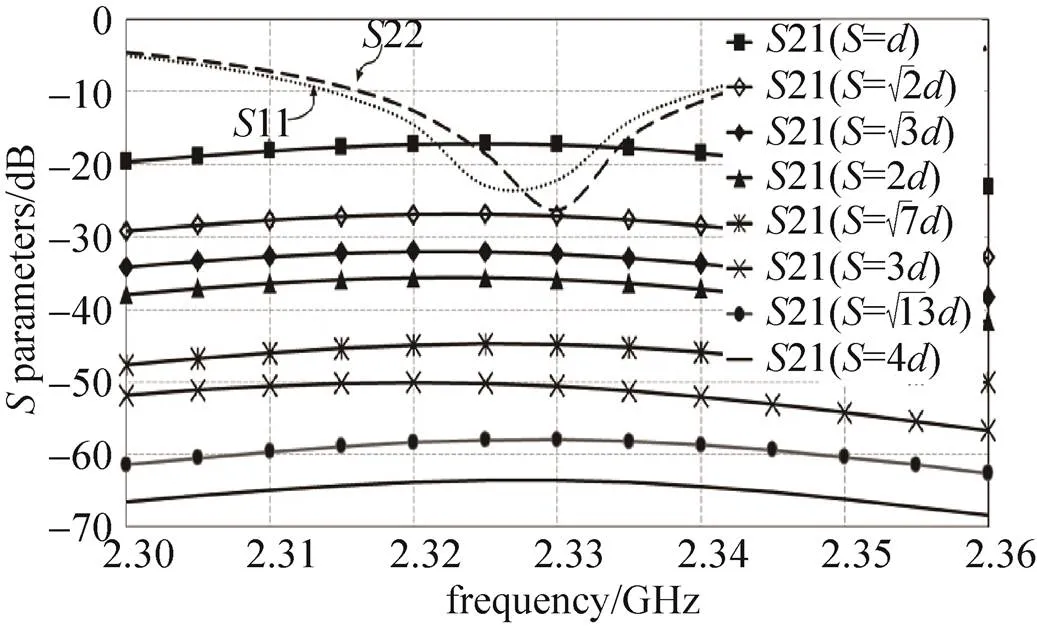
图11 互耦效应S21和天线间距S之间关系

3.2 接收信干比

通过使用时隙着色分配算法，多个天线阵元能够同时进行电性能校正，发射阵元的一跳邻居除了从该发射阵元接收期望的校正信号外，也接收其他发射阵元的干扰信号，仿真评估其校正信号的信干比SIR（Singal to interference ratio）是必要的。

设定相邻阵元之间距离为，考虑到接收阵元被干扰的最强和最弱两种情况，评估其校正信号的SIR。校正和干扰信号由每个阵元发射产生，它们具有相同的频率、相位和强度，所有信号在经过不同的传输距离后，在阵列中心的接收阵元处进行矢量叠加并耦合。可在具有不同拓扑结构和阵元数量的阵列上进行仿真。图12中实线代表接收阵元位于阵列中心，虚线代表接收阵元位于阵列左上角。无论阵列拓扑如何，校正信号的SIR在阵列规模达到12×12之后趋于稳定，最低SIR为14dB。

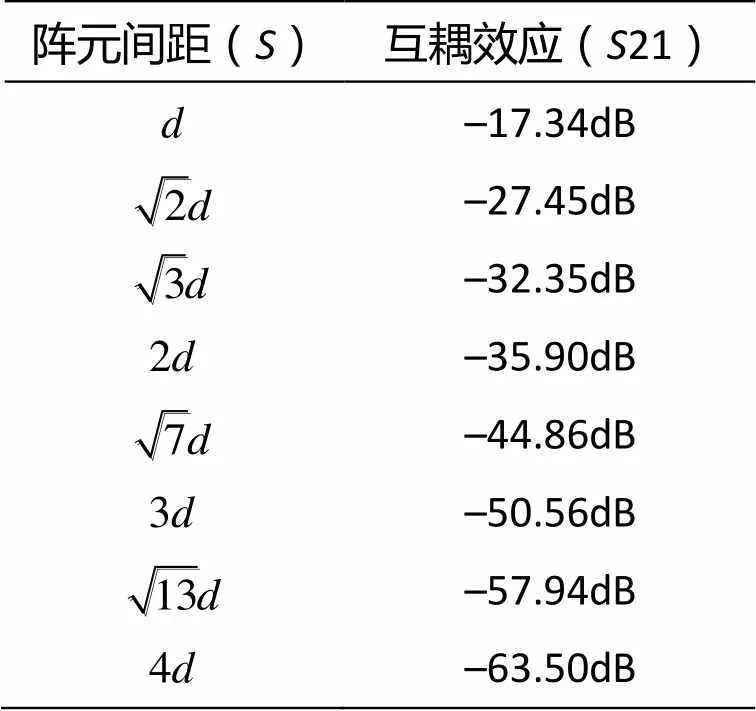
表4 频率2.33GHz时互耦效应和两阵元间距的关系

3.3 校正时隙总数仿真

采用Microsoft Visual Studio 2010软件，对校正时隙总数与阵元数目之间的关系进行仿真，仿真结果如图13所示。当阵列规模较小时，校正时隙总数随着阵元数目的增加而增加，当阵元数目继续增长时，所需的校正时隙很快趋于平稳。正六边形、正方形和正三角形拓扑阵列所需要的最大校正时隙总数分别为8个、9个和16个。表5列出了其他阵列校正方法所需的校正时隙数，当阵元数目足够多时，采用时隙着色方法所需要的校正时隙数最少。

图14为阵元不同失效率下的总校正时隙数量仿真结果。阵列规模为12×12的正方形拓扑阵列。随着阵元失效率的增加，总校正时隙减少。这是因为每一个阵元可用的校正时隙数都受到它的三跳之内的邻居阵元的限制。而当它的一部分邻居阵元失效时，这些三跳以内邻居阵元所占据的校正时隙就会被释放出来从而可以被该阵元所使用。

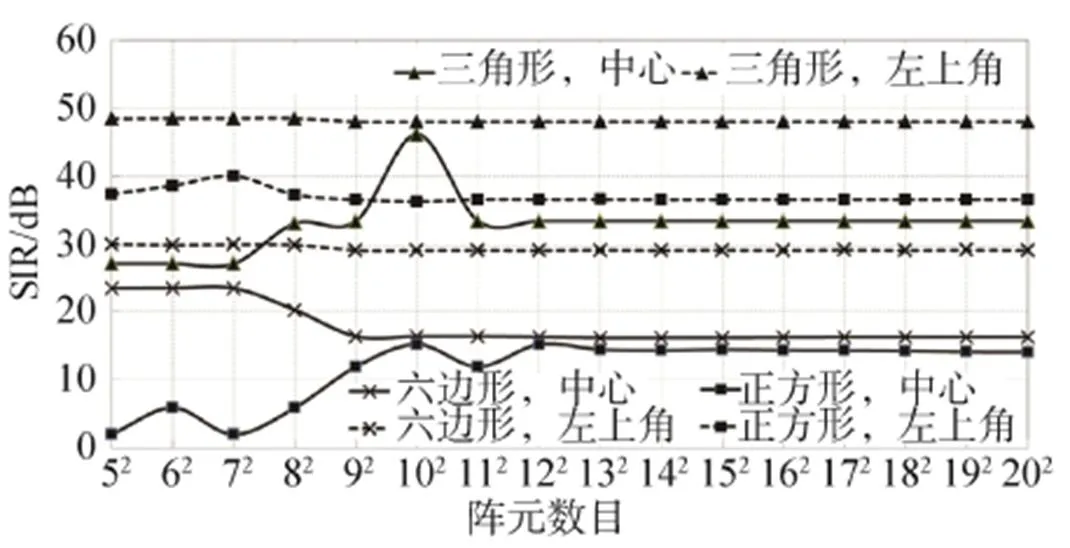
图12 校正信号的SIR和阵元总数之间关系

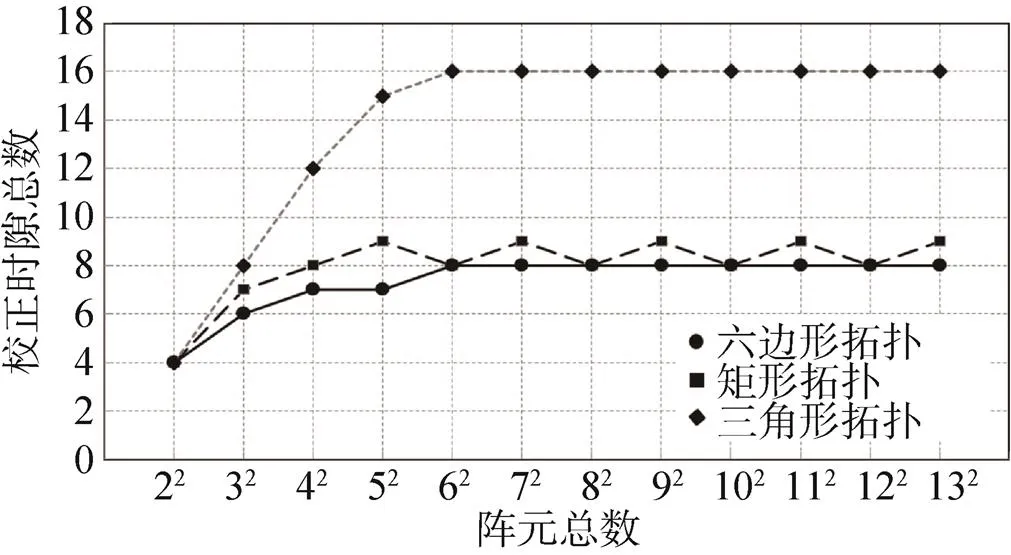
图13 不同阵元拓扑结构及数目校正时隙仿真图

表5 不同算法所需要的总校正时隙对比

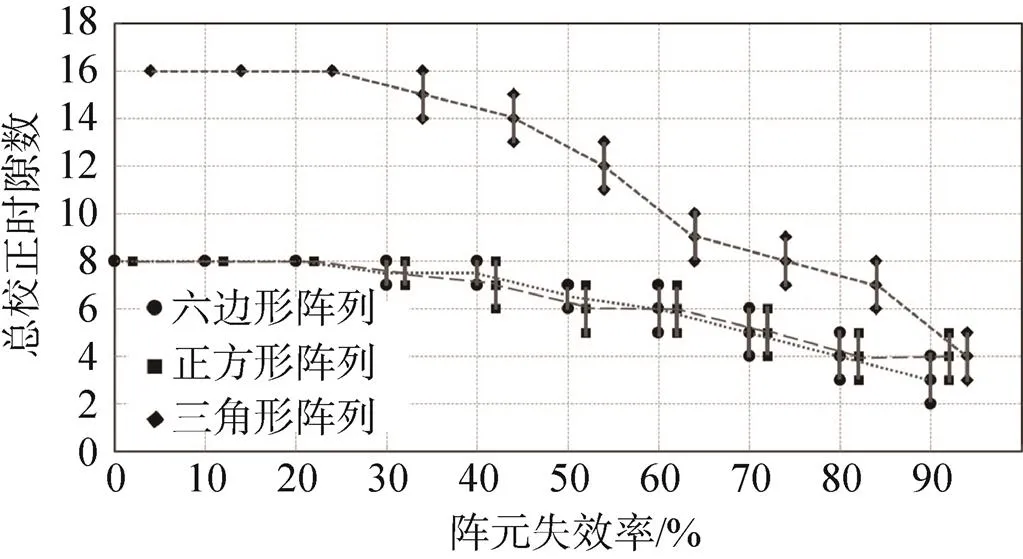
图14 阵元不同失效率的总校正时隙数量仿真

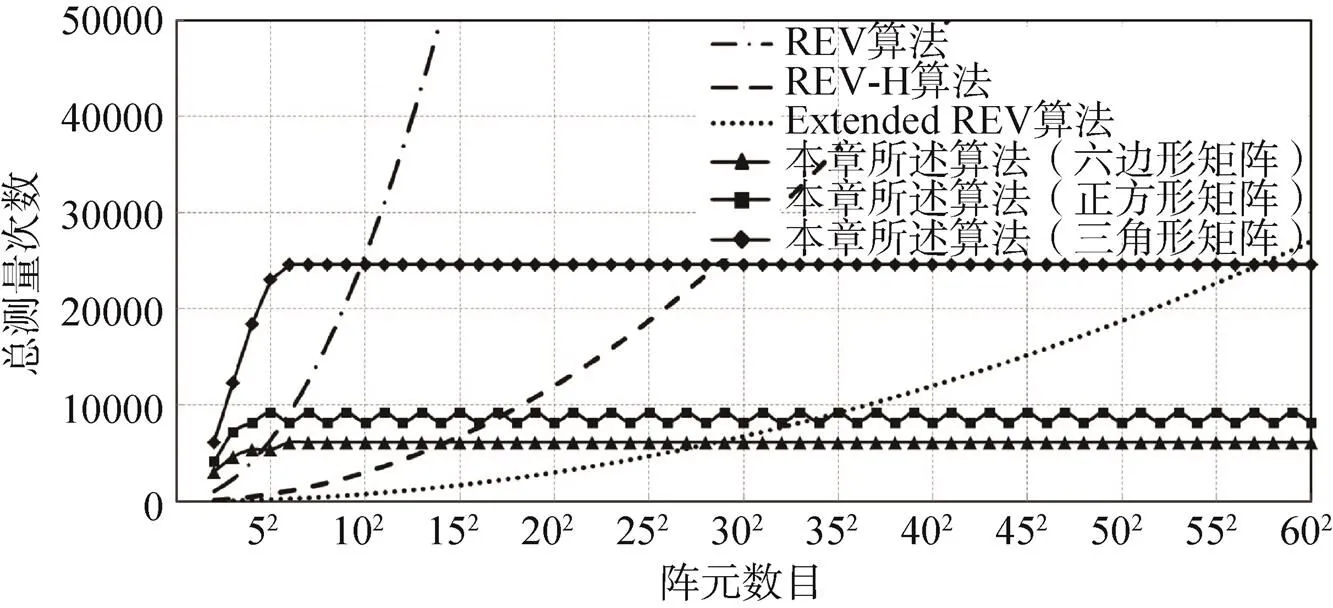
图15 不同拓扑结构、不同算法所需要的总测量次数

图15比较了不同校正算法所需的阵元测量总数，与REV算法相比，REV-H算法有更少的测量数，在REV算法中，每个校正时隙仅需要30次相移操作，而校正时隙总数等于阵元数量，测量总数为30。Extended-REV算法的测量总数至少为7.5+1。

本文利用图着色算法将总校正时隙从减少到不超过16个，测量总数为256××，其中256表示每个阵元相移步进量。表示校正时隙总数，取值参见图13所示。表示执行一次局部校正时，阵元相移的循环次数，值取决于阵列拓扑。以正方形为例，当阵元被激活执行局部校正时，每一个一跳邻居阵元都要重复一次相移操作，因此=4。与此类似，正六边形和正三角形拓扑阵列的分别为3和6。仿真表明当阵元数目很大时，时隙着色算法优势明显。

表6 不同拓扑结构、不同算法所需总测量次数

3.4 阵列天线辐射方向图仿真

图16为时隙着色算法校正前后的阵列天线辐射方向图，阵列拓扑为12×12的正方形平面。图16（a）是不存在幅度相位误差时的辐射方向图，完全中心对称，最大旁瓣比主瓣低13.05dB；图16（b）是存在每阵元幅度和相位误差且没有采取任何校正的辐射图，与图16（a）相比图16（b）的主瓣降低1.24dB，且最大旁瓣比图16（a）高1.15dB；图16（c）为经过时隙着色方法校正后的阵列天线辐射方向图，相比图16（b）主瓣改善了0.92dB，最大旁瓣功率下降了0.69dB。此外，校正后的阵列辐射方向图的平均旁瓣也远低于未校正时的辐射方向图。

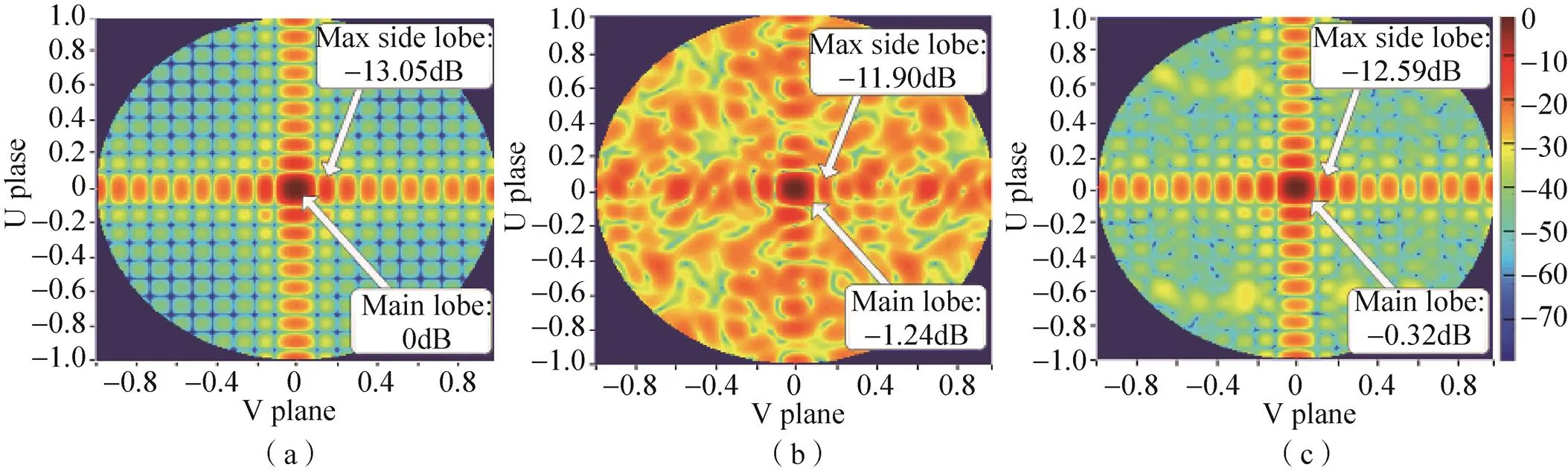
图16 时隙着色方法校正前后阵列天线辐射方向图对比

4 结束语

本文应用数学图论概念和方法，提出了一种基于时隙图着色的阵列天线校正方法，将天线阵元映射为图的顶点，将相邻阵元间的互相耦合效应映射为图的边，建立了阵列天线校正的图论模型，将校正时隙的分配问题转化为图论中的着色问题。优化目标是在确保校正信号信干比满足要求的前提下，尽可能减小所使用的校正时隙数；在整个天线拓扑结构未知的情况下，通过相邻阵元间广播的形式进行信息交换，以获得三跳以内邻居阵元的信息列表，并据此进行满足信干比要求的校正时隙分配。仿真结果表明：和传统的REV算法及其改进算法相比，该算法能够大大减少大规模阵列天线的校正时间，且随着天线阵元数目的增加，总体校正时间也趋于稳定。

[1] FULTON C, YEAR M, THOMPSON D, etal. Digital phased arrays: challenges and opportunities[J]. Proceedings of the IEEE, 2016, 104(3):487–503.

[2] HE Chong, LIANG Xianling, GENG Junping. Parallel calibration method for phased array with harmonic characteristic analysis[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(10):5029–5036.

[3] CASTILLO J, SANCHEZ S, PORRAS R, et al. L-Band digital array radar demonstrator for next generation multichannel SAR systems[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2015, 8(11): 5007–5014.

[4] ANSELMI N, SALUCCI M, ROCCA P, et al. Power Pattern sensitivity to calibration errors and mutual coupling in linear arrays through circular interval arithmetics[J]. Sensors, 2016, 16(6).

[5] CHEN B, OUYANG J, WU G, et al. A novel on-board and amplitude-only measurement method for phase array calibration[C].IEEE 5th Asia-Pacific Conference on Antennas and Propagation (APCAP), 2016-07-26:221–222.

[6] TAKAHASHI T, KONISHI Y, CHIBA I. A novel amplitude-only measurement method to determine element fields in phased arrays[J]. IEEE Transactions on Antennas and Propagation, 2012(60):3222–3230.

[7] SORACE R. Phased array calibration[J]. IEEE Transactions on Antennas and Propagation, 2001(49):517–525.

[8] TAKAHASHI T, KONISHI Y, MAKINO S, et al. Fast measurement technique for phased array calibration[J]. IEEE Transactions on Antennas and Propagation, 2008(56):1888–1899.

[9] XIE T, ZHU J, LUO J. The simplified REV method combined with hadamard group division for phased array calibration[J]. IEICE Transactions on Communications, 2018, E101.B:847–855.

[10] ERGEN S, VARAIYA P. TDMA scheduling algorithms for wireless sensor networks. Wireless Networks,2009(16):985–997.

[11] SAIFULLAH A, XU Y, LU C,et al. Distributed channel allocation protocols for wireless sensor networks[J]. IEEE Transactions on Parallel and Distributed Systems. 2014(25):2264–2274.

[12] DING Kaiqi, ZHAO Haitao, HU Xiping, et al. Distributed channel allocation and time slot optimization for green internet of things[J]. Sensors, 2017, 17(11):2479.

[13] ZHU Xudong, DAI Linglong, WANG Zhaocheng.Graph coloring based pilot allocation to mitigate pilot contamination for multi-cell massive MIMO systems[J].IEEE Communications Letters, 2015,19(10): 1842–1845.

[14] AGGELIKI S, DIMITRIOS J V, DIMITRIOS D V. A survey of TDMA scheduling schemes in wireless multihop networks. ACM Comput[J]. Surv. 2015,47(3): 53:1–53:39.

[15] YANG T, ZHANG R, CHENG X, et al. Graph coloring based resource sharing (GCRS) scheme for D2D communications underlaying full-duplex cellular networks[J]. IEEE Transactions on Vehicular Technology. 2017, 66(8): 7506–7517.

[16] BRÉLAZ D. New methods to color the vertices of a graph[M]. Communications of the ACM,1979, 22(4):251–256.

Method of phased array antenna calibration based on graph coloring theory

GAO Weibin1, DANG Ruirui2, YANG Lijie2

（1. Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, China; 2. Marine Electronics and Intelligent System Laboratories, Zhejiang University, Zhoushan 316021, China）

Phased array radars are able to provide highly accurate surveillance and tracking performance if they are properly calibrated. However, the ambient temperature variation and device aging could greatly deteriorate their performance. Currently, performing a calibration over a large-scale phased array with thousands of antennas is time consuming. To facilitate the process, we propose a fast calibration method for phased arrays based on the graph coloring theory. This method transforms the calibration problem into a coloring problem that aims at minimizing the number of used colors. By reusing the calibration time slots spatially, more than one antenna can perform calibration simultaneously. The simulation proves the total calibration time slots consumed by the proposed method are 8, 9 and 16 for arrays with hexagonal topology, square topology and triangular topology, respectively.

Graph coloring theory; Array calibration; Phased array; Amplitude and phase errors

TN952

A

CN11-1780(2019)03-0001-10

高卫斌 1967年生，硕士，研究员，主要研究方向为航天跟踪、测量与控制。

党锐锐 1991年生，硕士，主要研究方向为相控阵列射频前端电路设计。

杨李杰 1991年生，博士，主要研究方向为相控阵列校正技术。

2019-04-30

2019-05-12

TEL:010-68382327 010-68382557

Email:ycyk704@163.com