轮对柔性对车辆动态曲线通过性能的影响研究

李国芳,岳 鹏,丁旺才,王红兵,卫 佳

(兰州交通大学机电工程学院,兰州 730070)

随着我国高速列车不断提速，将车辆部件看作刚体来分析车辆系统的稳定性、安全性的传统做法已不能满足要求，因此引入柔性多体动力学理论，将车辆系统的某一部件考虑为柔性体后分析对车辆系统的动力学性能响应，这样做可以更深入地了解车辆部件的弹性效应对车辆系统各项动力学性能指标的影响，可使仿真分析更加贴合实际，结果更加准确，将轮对考虑为柔性体[1]正是在这种大背景下提出来的。由于轮对大角度旋转及轮轨接触关系的特殊性，使得考虑轮对为柔性的刚柔耦合建模较为复杂。近年来，对柔性轮对动力学模型的研究逐渐增多，主要集中在轮轨接触及其对车辆运行稳定性、轮轨磨损及噪声等的影响方面。N.Chaar和M.berg[2-3]研究了柔性轮对在0～100 Hz的频率范围内，对轨道力的影响并与实测值进行了对比，结果表明：轮对柔性对横向力和垂向力均有显著影响，与实测值吻合较好。Zhong Shuoqiao等[4]提出了一种与柔性轮对接触的轮轨耦合方法，并将其应用到传统的车辆轨道动态系统模型中，研究了轮对弯曲和轴向变形对轮轨滚动接触行为的影响并进行了数值分析。Lu Zhenggang等[5]建立了柔性轮轨接触模型，研究得到轮轨的结构振动对其接触点的位置、蠕滑力、轮轨力和脱轨系数影响显著。I.Kaiser和K.Popp[6]对比分析了轮对柔性与刚性时对仿真结果的影响，当列车行驶速度低于临界值时，柔性轮对的横向振动衰减速度慢于刚性轮对且振幅较大，结果表明轮对柔性时会降低车辆系统的临界速度。高浩等[7]介绍了一种基于传统迹线法思想的轮轨接触方法，并将其应用于考虑轮对柔性变形的动力学仿真，计算了轮轨接触点的位置和轮轨蠕滑率。万鹏等[8]，万涛[9]，郭训等[10]，贺建功[11]结合有限元分析软件ANSYS和多体动力学软件SIMPACK建立了考虑轮对柔性的车辆刚柔耦合动力学模型，对比分析了轮对柔性与刚性的动力学响应，吴正习等[12]在此基础上得到了车轮的动载荷响应并分析了车轮的疲劳寿命。在车辆系统通过曲线路段的过程中，轮轨的工作状态较直线路段更加复杂严苛，所以脱轨一直是影响车辆动态曲线通过的中心问题[13]。孙明昌等[14]建立了弹性轮对车辆-轨道垂向耦合系统动力学仿真模型，对比了不同速度时刚性轮对与弹性轮对的轮轨力。李国芳等[15]基于UM建立了车辆-轨道垂向耦合动力学模型，仿真分析了车辆的非线性临界速度、脱轨系数、振动加速度及平稳性指数等动力学特性。

本文基于多体系统刚柔耦合动力学理论[16-17]，通过ANSYS对轮对进行柔性化处理，运用多体动力学软件UM建立了考虑轮对为柔性的某型高速车辆刚柔耦合动力学模型，探究了轮对的弹性变形对车辆动力学性能的影响，对比分析了刚性轮对与柔性轮对的车辆系统动态曲线通过的各项安全性能指标及平稳性指标。

1 建立刚柔耦合动力学模型

1.1 柔性轮对有限元模型

借助三维建模软件Solidworks建立轮对模型，导入到有限元分析软件ANSYS中做柔性化处理。轮对采用Solid185三维实体单元，网格划分后共有46 485个节点，37 623个单元，设置2个mass21单元。轮对有限元模型如图1所示。

图1 轮对有限元模型

1.2 柔性轮对模态求解

在ANSYS中建立轮对有限元模型后，设置2个界面节点，采用Craig-Bampton法求解轮对的本征模态和静模态。计算轮对的前14阶模态，由于前6阶刚体模态为零，故将其去除，轮对的后8阶模态频率和振型如表1所示。

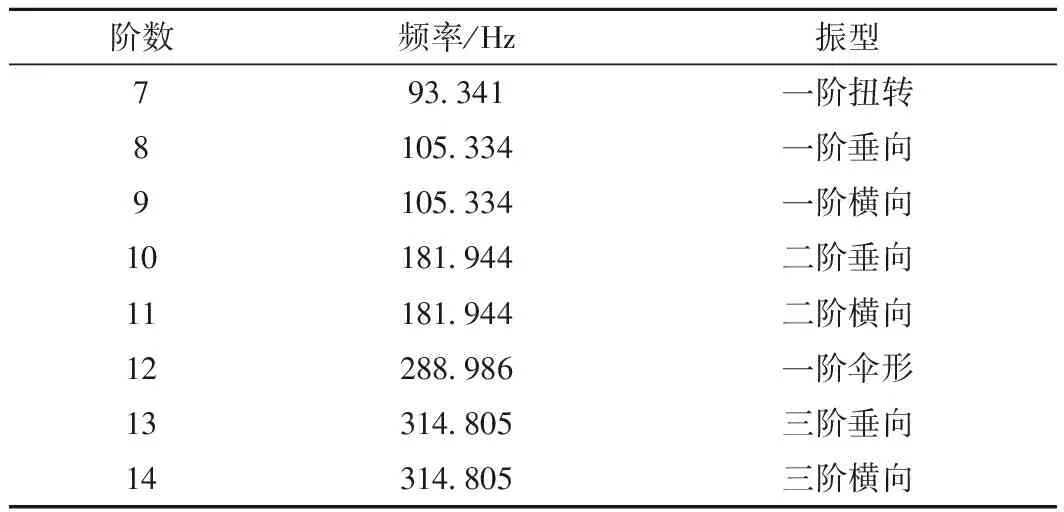
表1 轮对前8阶模态及振型

1.3 刚柔耦合动力学模型

借助UM中FEM模块来将柔性体引入到机械系统中，每一个柔性体被认为是一个单独的子系统，其借助铰和力元与其他刚体或柔性体相互作用。通过UM_ANSYS接口程序计算轮对的质量矩阵和刚度矩阵生成.fum文件，去除刚体模态后生成.fss文件，从而将轮对有限元模型导入到UM Input中，轮对柔性化处理步骤如图2所示。

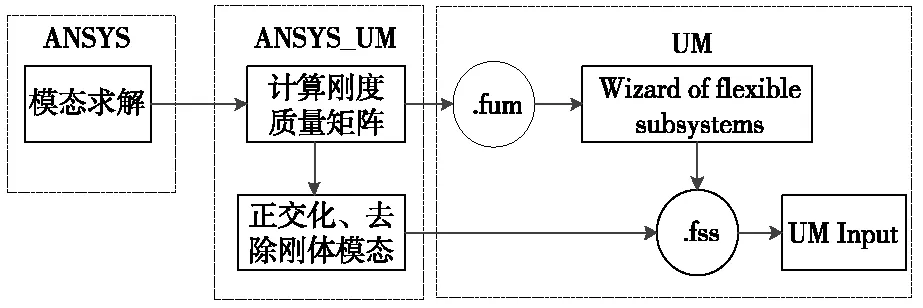
图2 轮对柔性化处理过程

将轮对有限元模型导入UM Input后，遵循体、铰、力元的规则，建立考虑轮对为柔性的某型高速车辆刚柔耦合动力学模型。车辆主要参数如表2所示，动力学拓扑图如图3所示，刚柔耦合动力学模型如图4所示。

表2 车辆动力学模型主要参数

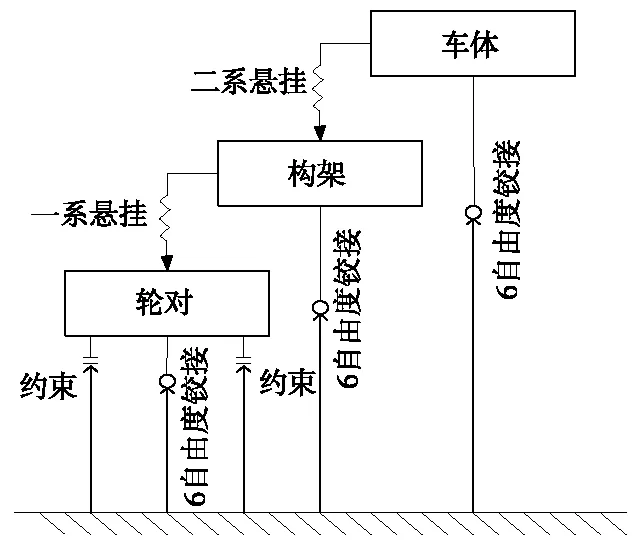
图3 动力学模型拓扑图

图4 车辆刚柔耦合模型

1.4 刚柔耦合动力学理论

1.4.1 柔性体运动描述(图5)

由于柔性体拥有无限多的自由度，所以无法利用连续力学方法求其解析解，故将其离散化，离散成有限个节点，通过节点的自由度来描述柔性体的变形[18]。

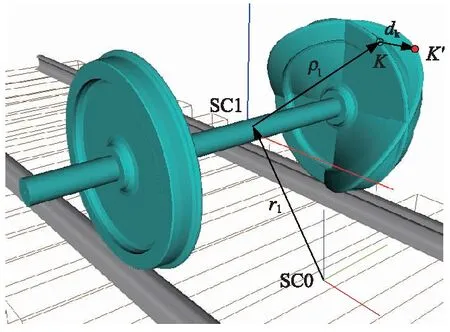
图5 柔性体空间描述

如图5所示柔性轮对，其上任意一点K在绝对坐标系SC0中表示为

(1)

用模态振型叠加表示K点微小的弹性位移

dk=Hkw

(2)

式中，Hk∈RN×H为在模态集中提取出与K点相关的模态矩阵；w∈RH×1为模态坐标；N为有限元模型自由度的个数；H为所选模态阶数。

1.4.2 刚柔耦合动力学方程

车辆刚柔耦合系统中通过铰与力元连接刚性体和柔性体，根据达郎贝尔原理和虚功原理，其动力学方程为[19]

(3)

式中，M、D、K分别为系统广义质量、阻尼、刚度矩阵；Cq为Jacobi矩阵；Q为广义力向量。

2 动态曲线通过性能分析

车辆在轨道不平顺等因素的激扰下，高速通过曲线路段时，轮轨间会产生复杂的动态作用力。以德国低干扰谱UIC_good作为轨道激励输入，车辆系统运行速度为200 km/h，选用LMA型踏面和CN60轨，以车辆动力学模型的1位轮对为研究对象，在不同的曲线工况下，对车辆多刚体动力学模型和刚柔耦合动力学模型的动力学响应进行对比分析，研究车辆的动态曲线通过性能。

根据铁运[2008]28号《高速动车组整车试验规范》及TB10621—2014《高速铁路设计规范》对车辆系统的各项动力学性能指标限定值[20-21]如表3所示。

表3 我国高速客车动力学性能指标执行标准

2.1 设置曲线工况

为了对比研究多刚体动力学模型和刚柔耦合动力学模型在通过曲线时的动力学行为，仿真计算时设置了半径不同的6种曲线工况，如表4所示。

表4 设置曲线线路工况

2.2 脱轨系数

车辆系统在通过曲线时，对脱轨安全性的评价和监测是确保车辆安全运营的关键。如图6所示，Nadal提出在脱轨临界状态下，作用在轮轨接触点上的垂向力Fz、横向力Fy、钢轨对轮轨接触点的法向力N、防止车轮向下滑动给轮轨接触点的摩擦力Fcy处于平衡状态，设轮缘角为δ，由此可以建立轮轨接触点处法线方向和切线方向的平衡方程[22]。

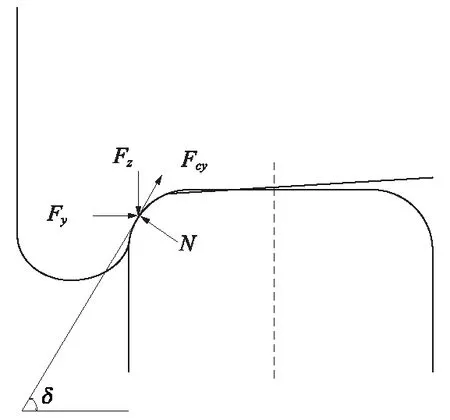
图6 车轮脱轨临界状态下轮轨接触点受力分析

其中Fcy=μN，求解方程(4)，可得

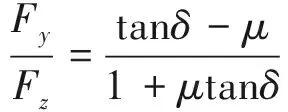
(5)

两种模型的脱轨系数比较如图7所示，可以看出，刚柔耦合动力学模型的脱轨系数较多刚体动力学模型要小，两种模型的脱轨系数在工况4处差值最大，降幅为38.1%，在工况2处差值最小，降幅为30.1%。

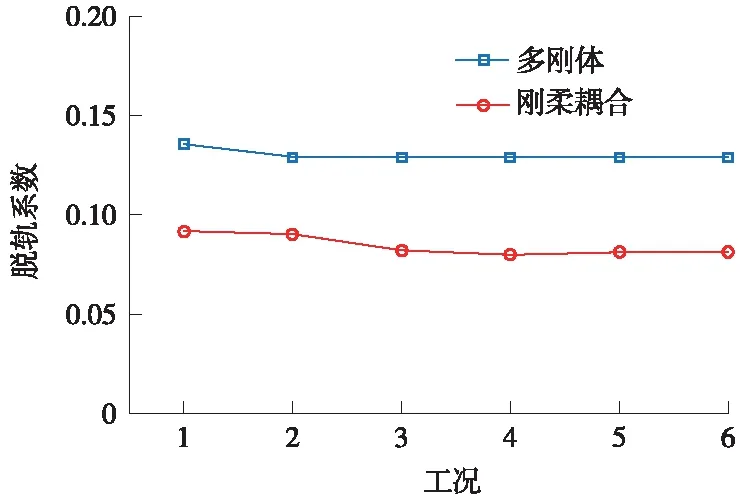
图7 两种模型的脱轨系数比较

本文工况设置中最小的曲线半径为3 500 m，当多刚体动力学模型通过上述工况时，车辆系统的最大通过速度为275 km/h，此时的脱轨系数为0.249，轮重减载率为0.749。由此看出，车辆系统的脱轨系数虽然较小，但其轮重减载率却接近于限定值0.8，而轮重减载率大的时候往往比脱轨系数大的时候更容易发生脱轨。

2.3 轮重减载率

当车轮大幅度减载时，轮轨垂向力和横向力较小，由于测量误差的影响，很难求出正确的脱轨系数，故轮重减载率可以作为辅助评价指标综合评定车辆运行安全性[23]。计算公式如下

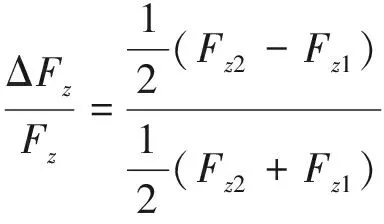
(6)

两种模型的轮重减载率比较如图8所示，可以看出，考虑轮对为柔性体后车辆系统的轮重减载率变小，两种模型1位轮对的轮重减载率在工况1处差值最大为0.036 5，降幅为7.7%，在工况3处差值最小为0.020 5，降幅为4.4%。

图8 两种模型的轮重减载率比较

2.4 轮轴横向力

对于线路来说，过大的轮对与轨道间的横向力将导致轨距加宽、轨排横移或钢轨翻转，增加线路的维修量，甚至危及行车安全；也会加剧线路的横向不平顺，从而影响车辆的运行平稳性[24]。根据文献[8]的相关规定，轮轴横向力最大允许值为

Hmax=0.85(10+P0/3)

(7)

式中，P0为静轴重， kN。由此可以得出该车辆系统的轮轴横向力最大允许值为48.2 kN。

由图9可以看出，考虑轮对为柔性体后使得车辆系统的轮轴横向力变小，两种模型的轮轴横向力在工况1处差值最大为3 753 N，降幅为34.5%，在工况6处差值最小为2 526 N，降幅为24.7%。

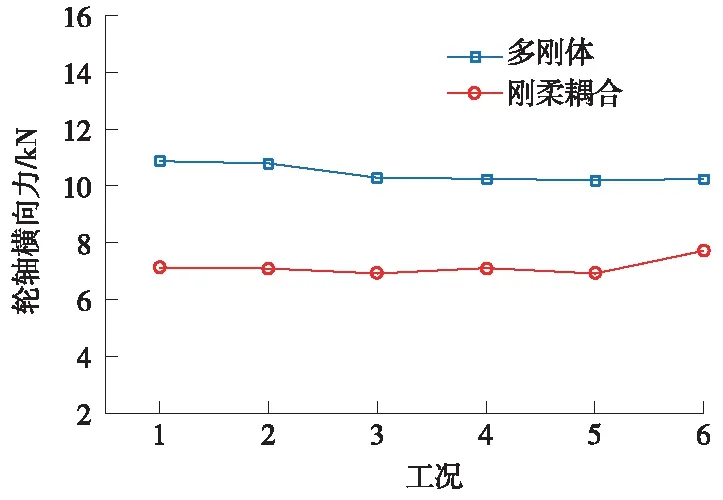
图9 两种模型的轮轴横向力比较

2.5 轮轨接触角

图10给出了工况5下车辆系统多刚体动力学模型和刚柔耦合动力学模型的轮轨接触角计算结果，可以看出，两种模型的轮轨接触角在小弧度0.05 rad和大弧度0.2 rad之间交替转换，由于两种模型的车轮踏面都为磨耗型踏面，从而得知，小角度时轮轨接触点发生在踏面处，大角度时轮轨接触点发生在轮缘根部处。

图10 工况5下轮轨接触角时间历程

由图11对比了车辆系统多刚体模型和刚柔耦合模型的轮轨接触角，可以看出，考虑轮对为柔性使得轮轨接触角增大，在工况1处增幅最大为40.4%，在工况2处增幅最小为4.0%。

图11 两种模型的轮轨接触角比较

2.6 轮对侧滚角位移

车辆系统通过缓和曲线时外轨上的车轮逐渐上升而内侧钢轨上的车轮保持高度不变，使得轮对的侧滚角逐渐加大，图12给出了工况5下车辆系统多刚体模型和刚柔耦合模型的轮对侧滚角位移计算结果。

图13对比分析了两种模型的轮对侧滚角位移，可以看出，考虑轮对为柔性体使得轮对侧滚角位移增大，且在工况4处增幅最大为0.18%，在工况5处两值相等，由此可见，轮对柔性对轮对侧滚角影响甚微。

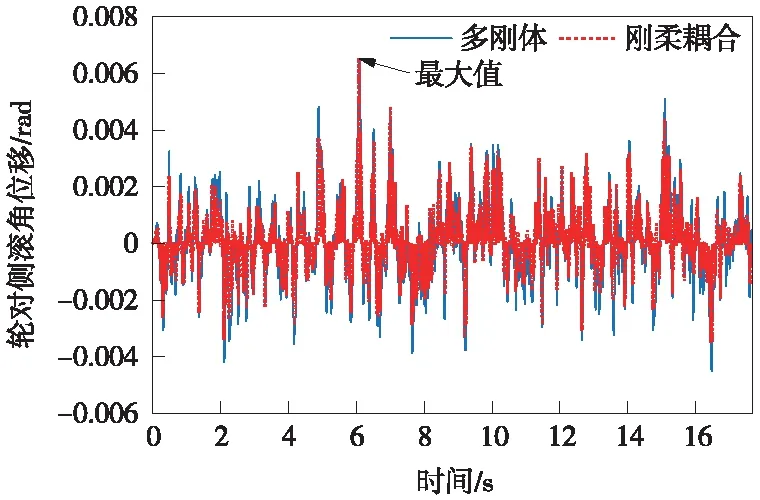
图12 工况5下轮对侧滚角位移时间历程

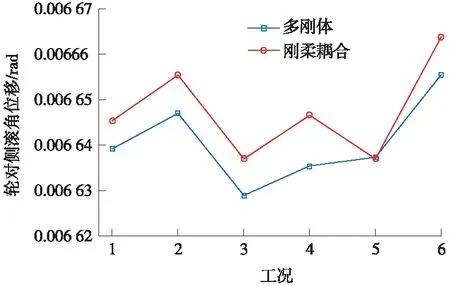
图13 两种模型的轮对侧滚角比较

3 平稳性分析

车辆系统在运行过程中，由于轨道接缝、道岔和轨道不平顺等干扰，引起车辆的振动评价从而影响旅客乘坐的舒适性。车辆乘坐的舒适性主要由车体振动加速度来予以评价。为了准确地评价车体乘坐舒适性，车体振动加速度的大小和频率都应当加以考虑，所以国际上广泛应用Sperling指标来评价车辆的运行品质和旅客乘坐舒适度。根据我国TB/T2360—93及GB5599—85标准规定，机车车辆平稳性计算公式见(8)式，平稳性评价等级见表3。

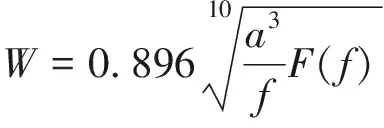
(8)

式中，a为振动加速度，cm/s2；f为振动频率，Hz；F(f)为与振动频率有关的修正系数。为了准确考查轮对为柔性时，对车辆系统动态通过曲线时的平稳性影响，计算点设置在转向架中心正上方车体地板面一侧1 000 mm处。

图14和图15分别为两种模型在工况5下运行时的车体横向和垂向加速度时间历程。

图14 工况5下车体横向加速度时间历程

图15 工况5下车体垂向加速度时间历程

分析图14和图15可知，车辆系统在通过曲线工况时，两种模型车体加速度的最大值均在第二段缓和曲线处出现，因为车体的振动主要与车辆本身一系、二系悬挂有关，轮对柔性对其影响较小，两种模型的车体振动加速度无论是曲线波形还是最大值均十分接近。

图16和图17分别为6种工况下车体最大横向加速度和最大垂向加速度的比较。

图16 两种模型的车体横向加速度比较

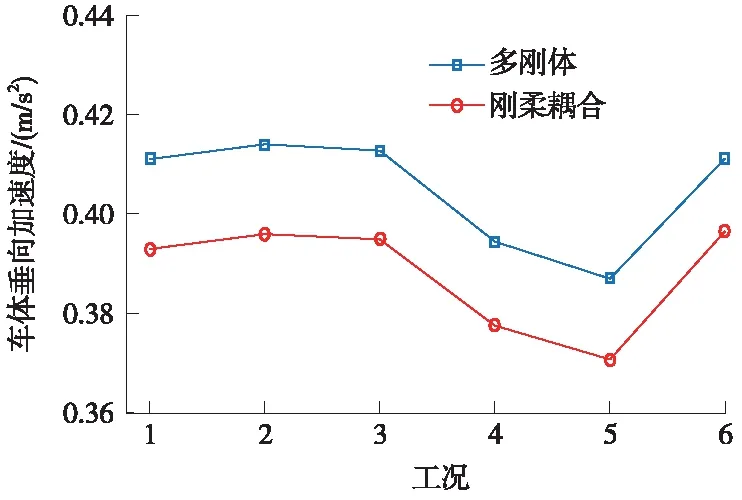
图17 两种模型的车体垂向加速度比较

由图16可以看出，刚柔耦合动力学模型的车体横向加速度较多刚体动力学模型要大，在工况2处两者差值最大为0.119 m/s2，增幅为9.3%，在工况4处两者差值最小为0.011 m/s2，增幅为1.1%。由图17可以看出，刚柔耦合动力学模型的车体垂向加速度较多刚体动力学模型要小，在工况2处两者差值最大为0.018 m/s2，降幅为4.3%，在工况6处两者差值最小0.015 m/s2，降幅为3.6%。

图18 两种模型的车体横向Sperling指数比较

由图18、图19可知，多刚体动力学模型和刚柔耦合动力学模型的横向Sperling指数分别在1.93～1.96和1.97～2.02波动，且两种模型在工况2处差值为最大，增幅为3.0%；多刚体动力学模型和刚柔耦合动力学模型的横向Sperling指数的波动范围分别是1.663～1.666、1.657～1.659，多刚体动力学模型的横向Sperling指数较刚柔耦合动力学模型较大且在工况3处差值最大，降幅为0.4%。

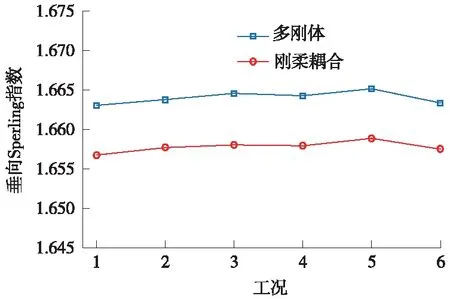
图19 两种模型的车体垂向Sperling指数比较

由此，两种模型Sperling平稳性指数的差异在3%以下，那么考虑轮对为柔性对车辆动力学系统的运行平稳性的影响不明显。

4 结论

本文基于多体系统刚柔耦合动力学理论，结合有限元软件ANSYS和多体动力学软件UM，建立了考虑轮对为柔性的某型高速车辆刚柔耦合动力学模型，对比分析了轮对刚性与柔性时车辆系统动态曲线通过时的各项安全性能指标及平稳性指标。借助有限元软件ANSYS，将轮对离散成有限个节点后，轮对变得“更软”，使得在车辆运行的过程中，对钢轨的冲击起到了一定的弹性缓冲作用，降低了轮轨作用力，提升了车辆的安全性能，因此车辆系统的各项动力学性能发生变化，得出以下结论。

(1)轮对为柔性时系统的脱轨系数、轮重减载率、轮轴横向力和垂向平稳性指数较轮对刚性时均有不同程度的降低。

(2)轮对为柔性时车辆系统的轮轨接触角、轮对侧滚角位移和横向平稳性较轮对为刚性均有不同程度的增加。

综上，考虑轮对柔性后，车辆系统的运行安全性能提升；车辆系统的运行平稳性却微幅下降。柔性轮对较刚性轮对更能真实地反映车辆系统的动力学性能。