基于扩展O-U模型的天气期权定价及数据信息应用分析

姚誉

摘要：天气期权不断发展，政府多次提出推广农产品“期权+期货”，天气期权在农业的应用成为研究重点。本文利用拓展的O-U模型，通过傅里叶变换、自回归方程、AR-GARCH等，以1951-2017年数据进行参数估计，预测大连市2018年的日均气温，吻合度较高，可应用于模拟期权定价。此外，分析其在玉米期权（GDDs、MGDDs）中应用的可行性和误差，并提出在农业中应用期权的建议。

关键词：天气期权;O-U模型;玉米期权

中图分类号：F832 文献标识码：A 文章编号：1007-9416（2019）05-0128-03

0 引言

随着全球气候变暖，气象灾害频发，异常天气事件对社会经济活动产生了严重影响。对天气敏感的企业，如：能源、农业、交通运输业、旅游业等均面临天气风险。其中，农业对天气的依赖性最强，因此，国外多采用天气衍生品、农业保险等多种综合手段来保障农民收益。我国也在加大对天气期权期货的研究试点。

天气衍生品市场正在不断发展，其中气温期权期货发展得最为迅速。气温期权将气温指数化模拟股指作为交易的标准。但由于气温指数本身的不可交易性，Davis（2001）等认为B-S模型不适用于天气类指数。此外，对气温的预测是气温期权定价的前期条件。Campbell（2005）用时间序列来进行天气预测，在短期和长期预测中都有具有可行性。李永（2011）中以上海市为例，进行了天气预测，精度检验极高，具有良好的预测效果。

本文运用李永（2013）的建模方法，以大连市为例，进行气温期权的分析研究。第一部分，是将1951-2017的日均气温数据作为时间序列，以扩展的O-U模型建模，包含季节、气温周期性变化、气温波动等因素。第二部分，采用傅里叶变换、自回归过程、AR-GARCH模型估计气温模型的各个参数。第三部分，拟合2018年的数据，进行精度检验，并模拟GDDs期权的定价及对冲农业风险的可行性。

1 拓展O-U模型

均值回归的Ornstein-Uhlenbeck过程的一般方程为：

dx（t）=-α（x（t）-μ）dt+σdw（t）                        （1）

本文将从季节变化、周期性变化、波动率来建立模型：

dTt=dSt+αtdt+σtdw（t）                             （2）

其中，Tt是大连市的第t天的日均气温，St是气温的总趋势，是对Tt的长期趋势拟合，α是均值回复速率，σt是各时期的波动率，w（t）是维纳过程。

1.1 长期趋势和季节变化

大连气温具有明显的四季变化，大体上呈现周期波动的情况，因此考虑通过傅里叶变换来拟合。其次，由于二氧化碳含量的逐年增加，用线性方程a+bt来表示温度的长期增长趋势。

St=a+bt+aisin+bicos  （3）

其中，m1，n1需要通过拟合1951-2017的数据来确定，傅里叶变换的级数。

1.2 均值回复速率

均值回复的速率需要通过分析Tt和St之间残差的关系，得到估计。由李永（2013）可知，气温一般存在自回归过程，用方程表示如下：

αt=ci（Tt-i-St-i）                                （4）

其中，p是具体回归的阶数，p的选择需要基于和AIC等准则和ACF、PACF的图像。

1.3 波动率

通常，夏季温度的变化较为稳定，而冬季温度相对变化幅度较大，因此，波动率不是一个常数。由于存在明显的季节性，所采用傅里叶变换表示大体趋势，方程表达如公式（5）。分析残差的自相关和偏自相关函数，考虑ARMA，方程表示如公式（6）。通过检验残差是否存在条件异方差，即ARCH效应。若存在该效应，则考虑AR-GARCH，方程表示如公式（7）：

Yt=d+disin（iωt）+ejcos（iωt）                 （5）

σt2=Yt+βi（σ2t-i-Yt-i）                          （6）

σt2=Yt+βi（σ2t-i-Yt-i）+γiσ2t-j+λkε2t-k（7）

其中，m2，n2可以通过具体数据，判断级数，q为AR的阶数，m3，n3是GARCH里的参数。

2 参数估计

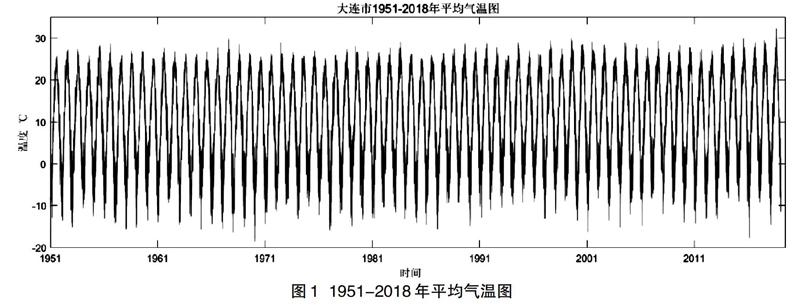
大连市逐日数据来源于中国气象数据网。时间区间为1951年1月1日-2018年1月1日，共24820项日均气温数据记录，其中2月29日数据都已删除，绘制如图1。为了对比分析预测精度，本区间选择为1951年1月1日-2017年1月1日，共24455项记录。

2.1 St参数估计

通過MATLAB编程，可估计St的各参数。通过比较多个m1，n1的组合，发现m1=n1=1时，误差最小，所以取值为1阶傅里叶。拟合后式（3）参数值如表1。

拟合后，如图2所示，模拟了日均气温的大致变化趋势。同时，对比了St所预测的2018年数据和真实数据，吻合度很高，如图3所示。

2.2 均值回复参数估计

从上一步得到Tt-St的残差值，将其记为Xt。为利用ARMA建模，对Xt进行平稳性的检验。在单位根检验法中，Xt的t统计值在-30.904，显著小于1%的临界值，-3.43，因此，不拒绝原假设，为平稳序列。

观察ACF，PACF图像（图4），有自相关函数呈拖尾状，偏自相关函数呈3阶截尾状，因此，建立AR（3）的模型，式（4）的参数估计如表2。

2.3 σt的参数估计

将1951-2017年中的样本数据，按照日期分为365组，每组有67条记录，计算每组的方差，可得到该日期的历史波动率，并通过不同傅里叶阶数组合，得到最适阶数为m2=n2=4，拟合如图5，式（5）参数估计值如表3。

对残值进行单位根检验，可以得到t统计量为-11.6513，1%的临界值为-3.448161，P值为0.0000，所以该残差序列为平稳序列，故进行ARMA回归。根据SIC准则，初步选定为AR（1），即一阶自相关性，因此，式（6），（7）中的q值应选为1。

一次残值拟合完AR（1）方程，得到二次残值。可以发现波动的集群现象，这说明二次残值可能存在条件异方差。利用ARCH-LM检验，结果如表4，通过比较，滞后阶数选为3。

上述结果表明，拒绝原假设，存在ARCH效应。利用GARCH消除条件异方差，通过分析，选定GARCH（1，1）模型，再次进行ARCH-LM检验，结果如表5。

上述结果表明，此时二次残值通过GARCH（1，1）消除了条件异方差。因此，选用式（7），参数q=m3=n3=1，参数拟合结果如表6。

其中，γ1和λ1的和为0.999634，小于1且都大于0，因此，满足参数约束条件。同时，两者之和充分接近1，说明二次残差序列的条件方差所受到的冲击是持久的，可以进行长期的预测。

此时，AR-GARCH模型的残差值偏度为0.137751，峰度为 3.317492，属于平顶分布，但是非常接近0，3，JB值为2.665262，所以该残差序列可以近似认为服从标准正态分布，满足模型εt～N（0，1）假设。

3 预测检验与定价应用

3.1 预测对比

将式（3）（4）（5）（7）代入式（2），并将各估计好的参数值代入，预测大连市2018年全年的日均气温，预测值与真实值的对比，如图7。预测值基本反映了温度的分布大体趋势，tf为预测值。

3.2 应用拓展

由于农作物各时期的生长要求温度并不相同，考慮利用分段的GDDs，以大连地区玉米为例。玉米在大连的播种时间一般为4月，收获时间为10月左右，根据生长温度的需求，将2月初到7月底，K=8℃，1月初到1月底和8月初到12月底，K=18℃。此时，真实值的GDDs指数为1699.5，预测值的GDDs指数为1511.867，相对误差项为-0.11041。误差较大，说明若要考虑分段GDDs，需要更高的预测精度。

4 结论及展望

本文利用拓展的O-U均值回复模型对大连市的温度进行预测，其中，涉及了傅里叶变换、自回归方程，AR-GARCH模型等。运用预测得到的2018年的气温值，分析了有关气温指数在农产品期权的可行性，得到以下结论：

（1）在气温预测的过程中，运用了傅里叶变换等，因此，还需要考虑Tt和σt是否协整，应进行协整检验。同时，随着天气期权市场的不断发展，气温的预测精度仍有待提升，气温预测是温值类期权的发展基础。（2）现有的玉米期权等对冲天气风险的针对性并不强。多数学者研究气温期权，在能源业应用结果较为成功，但在农业上应用还需综合考虑许多要素，亟待学者进一步研究。

参考文献

[1] M. Davis. Pricing weather derivatives by marginal value[J].Quantitative Finance，2001，1（3）.

[2] Cao M， Wei J. Pricing the weather[J]. RISK-LONDON-RISK MAGAZINE LIMITED-，2000， 13（5）：67-70.

[3] 刘国光.天气预测与天气衍生产品定价研究[J].预测，2006（06）：28-33.