内含报酬率的测算技巧
唐顺莉
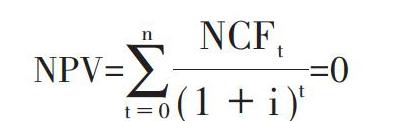


【摘要】 在常规项目每年净现金流量不相等的情况下,与传统逐步测试法相比,采用平均净现金流量法手工测算内含报酬率减少了计算步骤,但仍存在测试次数偏多、计算结果不够准确的特征;在具备电脑的环境下,采用Excel表格的IRR函数、单变量计算功能以及绘制净现值表测算常规项目和非常规项目的内含报酬率,比手工测算法的效率更高,计算结果更准确。
【关键词】 内含报酬率;IRR函数;单变量计算功能;净现值表
【中图分类号】 F232 【文献标识码】 A 【文章编号】1002-5812(2019)13-0064-04
一、内含报酬率的含义
内含报酬率(Internal Rate of Return,IRR)是项目投资决策常用的方法之一,它是使投资方案净现值为零的折现率。内含报酬率反映了企业投资项目资金成本的承受程度以及利率风险的承受水平。根据定义,其计算公式为:
NPV=[t=0nNCFt(1+i)t]=0
在该函数中,NPV 表示净现值;NCFt表示第t年的现金净流量;i表示基准折现率;t表示某个期间;n表示项目的预计使用寿命。
大部分项目在建设期发生初始投资,现金流出数大于流入数,净现金流量为负值,但进入营业期后出现经营收入大于经营支出,净现金流量为正值。因此,项目计算期内所有负现金净流量出现在正现金净流量之前的项目被称之为常规项目,如果其累计净现金流量大于零,则存在一个正实根,即为项目的内含报酬率。
部分项目如果在营业期间出现大量追加投资、在某些年份支出大于收入、或者在项目结束期产生诸如环境恢复相关的弃置费用等现金流出,都有可能导致项目净现金流量的符号在整个计算期内多次发生正负变化,这就形成了非常規项目。在这种情况下,可以通过笛卡尔符号规则来判断非常规项目内含报酬率方程根的个数。如果非常规项目内含报酬率方程有一个或者多个正实根,则必须对其进行数学检验,满足内含报酬率经济意义的正实根才是该项目的内含报酬率。如果没有正的实根或所有实根都不能满足内含报酬率的经济意义,则本项目没有解决方案。本文主要探讨内含报酬率的测算技巧,非常规项目内含报酬率的值是否有效,不在此处研究。
二、内含报酬率的传统测算技巧
(一)项目每年的净现金流量(NCF)相等
每年净现金流量(NCF)相等的项目实际上就是一个普通年金,我们可以使用普通年金现值公式,变形后求解年金现值系数,再利用查表和插值法求解。首先,计算年金现值系数:年金现值系数=初始投资额/每年NCF;接下来,根据上一步计算结果查年金现值系数表,在项目的投资期数确定的条件下,找到相近的较高和较低的两个年金现值系数及其对应的折现率;最后,采用插值法计算出IRR。
例1:宏达公司的某项目计算期一共5年,企业在该项目期初共投资200万元,从第一年开始,每年年末收回投资50万元,请求出该项目的内含报酬率IRR。
第一步:年金现值系数=200÷50=4。
第二步:按照项目的投资期数等于5查表,相近且高于4和低于4的年金现值系数分别为4.1002和3.9927,对应的折现率为7%和8%。
第三步:采用插值法计算内含报酬率(为了简化计算,设内含报酬率IRR为i%,详见表1)。
(i%-7%)/(8%-7%)=(4-4.1002)/(3.9927-4.1002)
解得:i%=7.93%,即IRR=7.93%。
从例1可以看出,如果项目每年的净现金流量相等,计算内含报酬率的步骤少,容易理解和运用。但在实际工作中,每年净现金流量相等的项目比较少,绝大多数是每年净现金流量不相等的项目。
(二)项目每年的净现金流量(NCF)不相等
在目前的财务管理教学过程中,如果项目每年的净现金流量(NCF)不相等,需要采用“逐步测试法”。第一步,根据经验预估一个折现率,按此折现率计算净现值,如果该净现值大于零,说明预估的折现率低于内含报酬率,应提高折现率的估计值,如果该净现值小于零,说明预估的折现率高于内含报酬率,应降低折现率的估计值;第二步,反复测试,找到由正到负并且比较接近于零的两个净现值及其对应的折现率。在测试过程中,可以根据预估折现率对应净现值的大小来判断下一次折现率估计数的区间,假如预估折现率对应的净现值为正数且远远大于零,应适当增大下一次预估折现率的距离,反之亦然;第三步,采用插值法计算出IRR。
例2:宏达公司的某项目计算期共5年,每年的现金净流量(NCF)如表2所示。
第一步:预估折现率10%,计算出NPV=360×(P/F,10%,1)+280×(P/F,10%,2)+500×(P/F,10%,3)+380×(P/F,10%,4)+350×(P/F,10%,5)-1 000=360×0.9091+280×0.8264+500×0.7513+380×0.6830+350×0.6209-1 000=411.17(万元)。
第二步:预估折现率15%,计算出NPV=244.82(万元)。
第三步:预估折现率20%,计算出NPV=107.71(万元)。
第四步:预估折现率25%,计算出NPV=-6.46(万元),净现值为负数,说明折现率估计过大,下一步应预估一个接近但低于25%的折现率。
第五步:预估折现率24%,计算出NPV=14.83(万元)。
第六步:折现率24%和25%对应的净现值分别为正值和负值,与其他值相比,两值更接近0,因此,采用插值法计算内含报酬率(为了简化计算,设内含报酬率IRR为i%,见表3)。
(i%-24%)/(25%-24%)=(0-14.83)/(-6.46-14.83)
解得:i%=24.70% ,即IRR=24.70%。
从例2可以看出,对于每年净现金流量不相等的项目,如果采用逐步测试法,可能需要较多的计算步骤,耗费时间较长。
(三)利用平均净现金流量手工测算内含报酬率
在实际工作中,为了减少测试步骤,缩小内含报酬率的试算区间,可以借助每年净现金流量(NCF)相等求解内含报酬率的思路,通过计算每年不相等现金净流量的平均数来求解内含报酬率,具体步骤如下:
首先,计算项目的平均净现金流量;其次,以平均净现金流量为年金,计算年金现值系数;再次,查年金现值系数表,在项目的投资期数确定的条件下,找到相近的较高和较低的两个年金现值系数及其对应的折现率i1和i2,依据i1和i2计算项目的净现值,如果恰好为一正一负,进入下一步;如果都为正值或者负值,测试接近i1和i2折现率对应的净现值,直到找到由正到负并且比较接近于零的两个净现值及其折现率;最后,采用插值法计算出IRR。
例3:沿用例2的资料,采用平均净现金流量法求解该项目的内含报酬率。
第一步:项目的平均净现金流量=(300+280+500+600+350)/5=406(万元)。
第二步:年金现值系数=1 000/406=2.4631。
第三步:在项目期数为5的时间里查出高于2.4631和低于2.4631的年净现值系数分别为2.4830和2.4356,相应的折现率分别为29%和30%。当折现率为29%时,NPV=360×(P/F,29%,1)+280×(P/F, 29%,2)+500×(P/F, 29%,3)+380×(P/F, 29%,4)+350×(P/F, 29%,5)-1 000=-84.59(万元)。折现率29%对应的净现值为较大的负数,故不需要再计算折现率30%对应的净现值,在该情况下,应试算小于29%且距离29%较远的折现率对应的净现值。试算折现率为25%时,NPV=-6.46(万元)。因为25%对应的净现值离0值相对较近,因此,降低折现率1%,测试折现率24%,得NPV=14.83(万元)。
第四步:折现率24%和25%对应的净现值分别为正值和负值,采用插值法计算出IRR=24.70%。
与逐步测试法相比,平均净现金流量法减少了内含报酬率的试算步骤,简化的工作内容。
(四)利用Excel表格测算内含报酬率
1.利用IRR函数求解。IRR(values,guess)用来计算返回的内含报酬率的数字。Values为项目计算期内一系列的现金流量,guess为对函数IRR计算结果的估计值。对于常规项目,一般不需要为IRR函数提供guess值,系统默认该值为10%。对于非常规项目,可能存在多个值,一次不能计算出全部的IRR,需要在IRR函数中加入参数guess,将其值从0.01开始逐渐递加,当加某个数时,IRR得到第二个解。
例4:沿用例2的资料,我们采用Excel的内含报酬率函数计算IRR,在Excel表的A2到A7分别输入年份,在B2到B7分别输入净现金流量,A8输入IRR,B8输入=IRR(B2:B7),得到项目内含报酬率的值为24.69%,该值与手工测算的24.70%相比,基本一致,但更精确。示例如图1左图。
利用IRR函数求解非常规项目内含报酬率可以用例5来说明。
例5:宏达公司的某项目在期初投资500万元,在营业期间,第1—4年的净现金流量分别为600万元、300万元、300万元、200万元,由于该项目有承担环境保护和生态恢复等义务所产生的支出,第5年末净现金流出1 000万元。请计算该项目的内含报酬率。
由于该项目净现金流量正負符号变化2次,故其存在2个根,属于非常规项目。对于IRR1的计算,可以参照例4常规项目的计算过程,得出IRR1的值为6.34%;在此基础之上,可从0.06逐渐递增guess值,增加到0.6,即得到IRR2=60.2%,示例如图1右图。
2.利用Excel表格的单变量计算功能。沿用例2的资料,我们采用Excel表格的单变量求解功能计算项目的内含报酬率。在例4数据表格的基础上,我们在B8输入0,A9输入NPV,B9输入=NPV(B8,B3:B7)-1000。选择菜单栏“数据”—“假设分析”—“单变量”求解,在弹出菜单的“目标单元格”中输入“B9”,“目标值”输入“0”,“可变单元格”输入“$B$8”,回车即可得到项目的内含报酬率为24.69%,见上页图2。
非常规项目亦可利用Excel单变量功能求内含报酬率,以例5的资料为例:按常规项目的求解方法求出第一个解6.34%后,改变B8单元格的初始值为1,再按前述步骤,求得IRR2为60.2%。因为 Excel表格中的单变量求解,只能得出一解,如需求其他值,可以通过改变可变单元格的初始值找到另外的解,可变单元格的初始值在0—1范围内改变使内含报酬率的值有意义。
3.绘制净现值表。除了采用IRR函数和单变量计算功能测算内含报酬率,还可以通过绘制净现值表测算内含报酬率。沿用例5非常规项目的数据,绘制净现值表。将项目净现金流量相关数据输入Excel表前两行中,如图3(左侧)所示。从第4行开始,在A4、A5中依次输入1%、2%,然后选择A4、A5,光标放在选中区域的右下角,当变成黑色“+”的时候,按住左键向下拉,填充到某个合适的折现率结束。如果项目需要,A4、A5的输入值也可以从负数开始。在列B4输入净现值计算公式“=NPV(A4,$C$2:$G$2) +$B$2”,从列B5开始复制B4公式,即可得到某个折现率对应的净现值。净现值恰好为0、净现值由正变负或者由负变正过程中对应的折现率即为内含报酬率。
从图3(左侧)可以看出,项目有两个净现值为0的根,折现率分别在6%~7%和60%~61%之间,进一步用插值法即可计算出准确的内含报酬率。亦可在净现值表格的数据基础上,利用Excel的绘图功能,绘制净现值曲线,如图3(右侧)。
五、评价
对于净现金流量不等的项目来说,虽然采用平均净现金流量法减少了传统逐步测试法的步骤,但仍存在计算量较大、计算不够准确的特征,特别是对于每年净现金流量差异较大的项目,平均净现金流量法测试的次数仍可能存在较多步骤。对于非常规项目来说,可能存在两个或者两个以上的根,手工计算平均净现金流量法就更显得更复杂。
利用Excel表格计算内含报酬率的三种方法极大地提高了内含报酬率计算的准确性和效率。如果项目为常规项目,运用IRR函数或单变量求解功能即可准确快速地求出项目内含报酬率,不必制作净现值表。如果项目为非常规项目,IRR函数可以通过不断修改guess值求出多解,如果多解的值差异较大,就存在测试次数较多的情况。单变量求解法通过改变可变单元格的初始值求出多解,运用相对方便。绘制净现值表的优点在于能够清晰表示每个折现率和净现值的关系,直观明了,容易理解。但运用这种方法,只能估计内含报酬率的范围,如要求准确值,还需要用插值法计算,与另两种Excel表格操作方法比,步骤相对较多。
考虑到上述方法的优缺点,在有电脑的环境下,建议采用Excel表格计算内含报酬率,常规项目优先选择IRR函数法和单变量求解法,非常规项目优先选择单变量求解和绘制净现值表法;在不具备电脑的环境下(比如考试),建议采用平均净现金流量法。
【主要参考文献】
[ 1 ] 冀聪慧.内含报酬率的求解及多解问题分析[J].商业会计,2016,(8):87-88.
[ 2 ] 郑宇梅,董艳萍,李荣耀.内含报酬率的求解技巧[J].财会月刊,2016,(1):115-116.
[ 3 ] 谭丽娜.内部收益率在企业投资决策中的运用[J].统计与决策,2012,(3):183-185.

