基于振动速度的柴油机缸内峰值压力提取方法研究

唐娟，胡云萍，魏庆檀，程勇

(1.聊城大学机械与汽车工程学院，山东 聊城 252000；2.山东大学能源与动力工程学院，山东 济南 250061)

柴油机作为广泛应用的动力机械装置，其燃烧性能直接决定了柴油机的动力性、经济性及排放性。对柴油机燃烧过程信息及时反馈并发现燃烧中存在的问题，对节能减排有重要意义。

缸内峰值压力是燃烧过程评价的重要特征参数之一，缸内压力是确定缸内峰值压力最有效的信号，但缸内压力的测量受传感器成本、安装和通道效应的局限难以实现在线应用。研究表明，发动机机体、缸盖等位置处的表面振动信号和缸内燃烧过程密切相关，且振动传感器安装方便、价格便宜，更容易实现在线测量。很多研究者开展了基于振动信号评价燃烧过程的研究。Barelli等[1]提取2 000 Hz以下的振动加速度信号用于反映燃烧过程信息，指出振动加速度的均方根随负荷的增大而增大，均方根变化可表征燃烧过程的剧烈程度；并以前100阶傅里叶分解信号的幅值平均值表征平均指示压力的变化，对各缸工作均匀性进行了评价。Taglialatela-Scafati等[2]指出燃烧能量主要反映在1 000～1 500 Hz的振动加速度信号中，加速度的幅值位置与缸内峰值压力出现位置和50%放热率时刻密切相关。刘世元等[3]利用燃烧时段振动加速度信号的正峰值及其持续时间来表征燃烧激励的强度波动特性和时间波动特性。本研究在前期分析了振动速度相位特征参数和燃烧始点、最大压力升高率出现时刻及缸内峰值压力出现时刻的理论对应关系，指出燃烧相位特征参数和振动速度相位特征参数存在相位差[4]。赵秀亮等[5]基于EMD方法重构加速度信号，研究了修正振动特征参数和燃烧特征参数相位差的方法。目前基于振动信号描述缸内峰值压力的研究还鲜有介绍。本研究基于振动速度和缸内压力的理论关系推导了描述缸内峰值压力的振动特征参数表达式，并验证了该方法的可行性，为利用振动速度定量描述缸内峰值压力提供了理论依据。

1 基于振动速度的缸内峰值压力描述方法

1.1 缸内峰值压力与峰值位移的关系

前期研究表明，燃烧激励引起的振动位移响应幅值(峰值位移)可线性表征缸内峰值压力的变化[6]。但因振动位移传感器测量频率过低，导致高频燃烧信息无法测量，能够测得的有效低频信息也容易被干扰信号淹没，因而基于实测的峰值位移难以实现缸内峰值压力的有效评价。振动速度是振动位移的导数，速度传感器测得的中低频信息足以反映燃烧过程信息。理论上可通过振动速度积分获取峰值位移，实现缸内峰值压力评价。

1.2 基于振动速度的峰值位移提取方法

1.2.1振动速度响应模拟

为排除其他激励及干扰信号影响，推导出描述峰值位移的方法，首先基于已验证的单缸柴油机有限元模型[6]模拟了1 200 r/min，30 N·m工况燃烧激励单独作用时的缸盖表面振动速度响应。图1示出模拟的一个循环的振动速度和实测缸内压力对比结果，图2示出燃烧上止点前后60°时段范围内的振动速度和缸内压力局部放大。

图1 一个循环实测缸内压力及模拟振动速度信号

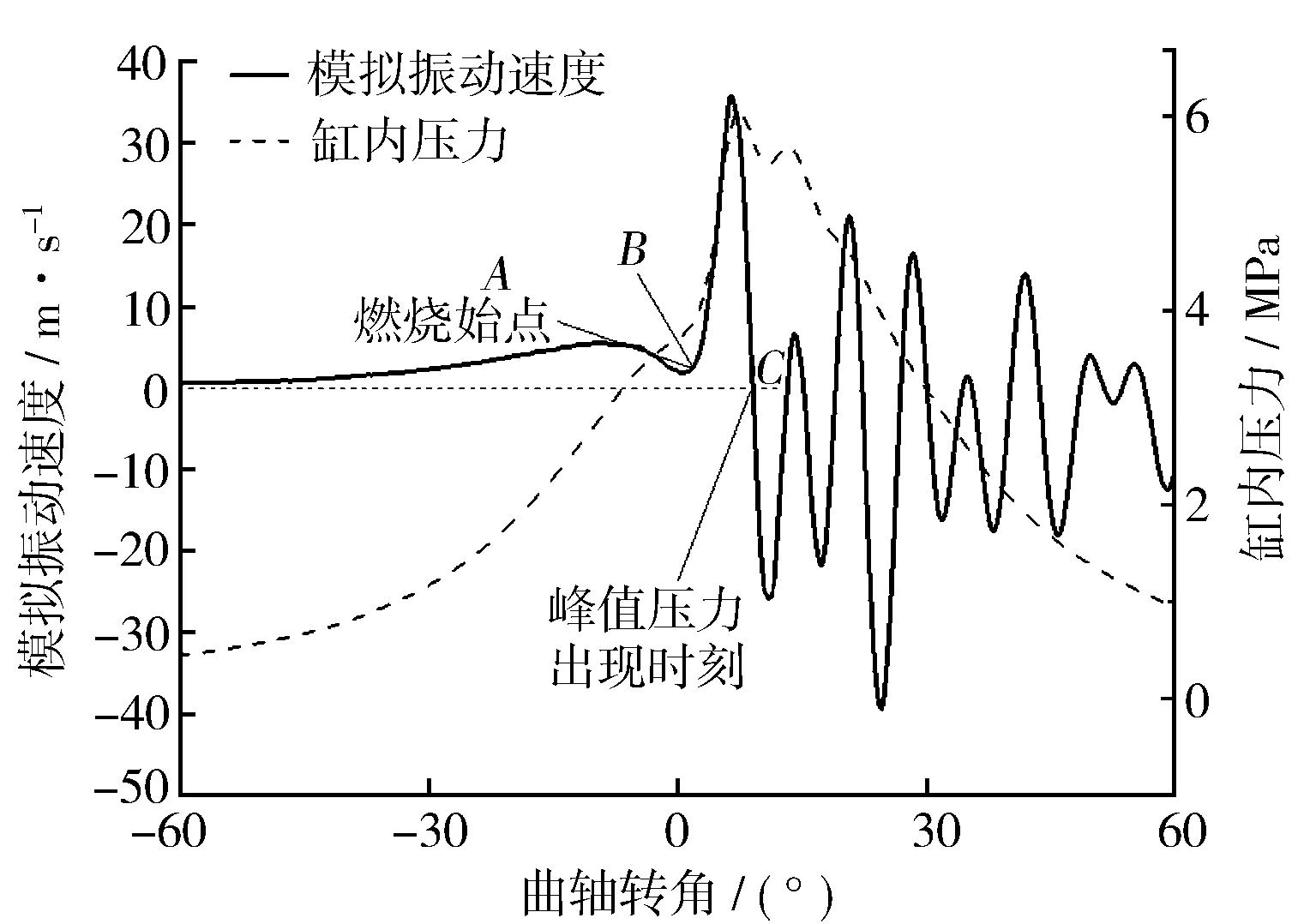
图2 燃烧时段局部缸内压力及振动速度响应

分析表明[6]：缸内峰值压力前，振动速度和压力升高率有相同的变化特点，图中A点为振动速度识别的燃烧始点，C点为振动速度识别的缸内峰值压力出现时刻，B点为A点之后的相邻点。为描述方便，采用s(t)表示振动位移，v(t)表示振动速度，t表示时间。实测振动信号为离散信号，当采样频率一定时，两采样点间的时间间隔一定，并设为Δt。

1.2.2振动速度积分时段选择

振动速度积分可得到振动位移，而峰值位移取决于积分时段的选择及积分初始位置处振动速度和振动位移。

如图1所示，无其他激励作用时，在进排气冲程阶段，缸内压力幅值几乎不变，v(t)幅值几乎为0，该阶段的振动速度积分结果为0，因此，可以忽略该阶段振动速度对积分峰值位移的影响。

如图2所示，进排气门关闭之后到燃烧开始之前的压缩冲程，缸内压力缓慢增加，压力升高率先增大后降低，相应的振动速度变化和压力升高率变化一致，先增大后减小。该阶段振动速度不为0，设该段振动速度积分结果为s0。对于同一发动机，相同转速下，即使工作负荷不同，理论上燃烧始点前的压缩过程也完全一致，因此，相应的振动速度响应也完全一致，此时，s0为常数。转速不同时，s0略有差异。这说明从压缩冲程开始到燃烧始点前的振动速度对峰值位移的提取有一定影响。

燃烧始点后，受缸内压力变化影响，振动速度幅值开始急剧增加，然后降低，当缸内压力达到峰值时，振动速度第一次到达零点C。从燃烧始点A到缸内峰值压力出现时刻C这一阶段的振动速度变化完全取决于缸内燃烧过程，因此，该阶段振动速度的变化是影响峰值位移提取的关键因素。

考虑到实测振动速度在压缩冲程中存在进气门关闭激励，该激励引起的振动速度响应会影响峰值位移的提取。因此，本研究选择燃烧始点A到缸内峰值压力出现时刻C这一曲轴转角范围内的振动速度响应作为计算峰值位移的基础。

1.2.3峰值位移提取方法

设从燃烧始点A到缸内峰值压力出现时刻C这一时段有n个采样点。A点振动速度设为v1，振动位移设为s1。B点的速度设为v2，位移为s2。

同理，设第i采样点的位移为si，则有

si=s1+v1·Δt+…vi-1·Δt。

(1)

以此类推，设C点对应的峰值位移为Smax，则Smax可表述为

(2)

式中：vi为不同采样点对应的振动速度。

由式(2)可知，Smax主要取决于燃烧时段的振动速度、采样间隔和燃烧始点位移s1。而式(1)说明第i点处的振动位移是i点前振动速度积分的结果，因此，燃烧始点的振动位移s1应是燃烧始点前振动速度积分的结果，即满足s1=s0。可见，燃烧始点前振动速度的影响已经体现在参数s1中，因此，取A到C点振动速度提取Smax合理。但s1难以测量，同一转速工况，s1为常数，不同转速工况，s1略有差异，结合式(2)可知，s1只影响Smax的基数，不影响Smax的变化。模拟结果表明，燃烧始点处的振动位移s1=0.025 mm。

1.3 峰值位移提取方法模拟验证

基于已验证的单缸柴油机有限元模型[6]模拟的1 200 r/min不同负荷工况下的振动速度响应结果见图3。由图可见，燃烧始点前，各振动速度响应曲线重合，进一步说明燃烧始点前的振动速度对积分结果影响可以忽略。基于式(2)提取不同负荷工况下的Smax，并和缸内峰值压力(pmax)进行对比，s1=0.025 mm时，计算结果见表1。由表可见，振动速度提取的Smax随pmax的增大而增大，表明基于振动速度提取的Smax能够描述出pmax的变化。

图3 不同负荷工况模拟振动速度响应

负荷/N·m10203040pmax/MPa4.315.496.287.02Smax/mm0.0270.0380.0430.050

图4示出了s1=0 mm和s1=0.025 mm时pmax和Smax的关系。结果表明，Smax和pmax为近似线性关系，根据两者关系，理论上可基于Smax实现pmax的定量评价。另外，s1对峰值位移和缸内峰值压力的比例关系影响可以忽略，为计算方便，后文取s1=0 mm。

图4 pmax和Smax的关系

2 试验验证及分析

2.1 研究对象及试验装置

为验证方法有效性及普适性，以1110和295柴油机为对象，分别测量了不同转速及不同负荷下发动机缸盖表面的振动速度和缸内压力信号。不同转速下，设置的1110柴油机负荷变化范围为0～50 N·m，负荷增量为10 N·m，295柴油机的负荷变化范围为0～100 N·m，负荷增量20 N·m。试验用传感器参数和发动机参数见表2和表3。试验用采集系统为USB2002数采系统，各通道采样频率均设为50 kHz。

表2 试验发动机参数

表3 试验用传感器参数

2.2 振动速度预处理

图5示出1110柴油机在1 400 r/min，50 N·m工况下实测的缸内压力和缸盖表面振动速度。由图可见，实测振动速度响应除在燃烧时段出现突变外，信号中还存在一个低频波动，该波动将影响峰值位移的提取，分析表明该波动的频率低于250 Hz，因此，对低频波动信号进行最小二乘拟合，实测振动速度减掉最小二乘拟合信号即为燃烧激励振动速度响应。上止点前后90°范围内处理后的振动速度响应见图6。由图可见，低频波动影响已去除。

图5 实测振动速度信号和缸内压力信号曲线

图6 处理前后的振动速度信号对比

2.3 峰值位移和缸内峰值压力对比结果分析

基于实测的缸内压力、式(2)和预处理后的振动速度，提取了1110和295柴油机在不同转速和不同负荷工况下的pmax和Smax，图7示出不同转速、不同负荷工况下对应的pmax和Smax关系曲线。

图7 1110和295柴油机pmax和Smax对比

首先，振动速度提取的Smax和pmax均随负荷的增大而增大，且Smax和pmax之间为近似线性关系，表明Smax可描述出pmax的变化。

其次，尽管对实测信号进行了预处理，但仍难以完全消除干扰信息的影响，同时因工况设置存在一定波动，导致实测振动速度提取的Smax存在一定偏差，同一转速下Smax和pmax对应关系曲线存在一定非线性度，但仍可近似为线性关系。

再次，同一机型不同转速下的Smax和pmax关系曲线不重合，即相同缸内峰值压力对应的不同转速下的峰值位移不同，分析认为这种偏差主要是因为在Smax的计算过程中s1取值相同导致的。

尽管各转速下Smax和pmax的关系曲线不重合，但各线段的斜率相近。表明对同一机型，Smax和pmax之间的比例关系是近似固定的。

为实现缸内峰值压力的定量评价，并减小s1对Smax的影响，以不同转速不同负载下的Smax和pmax数据为基础，采用最小二乘法对Smax和pmax之间的定量关系进行了线性拟合，结果见图8。根据图8所示线性关系，即可基于振动速度实现缸内峰值压力的定量评价。

图8 不同发动机pmax和Smax关系拟合曲线

不同机型对应的Smax和pmax关系曲线斜率存在一定差异。根据振动理论可知这种差异与发动机结构参数有较大关系，发动机结构参数对峰值位移和缸内峰值压力比例关系的影响将在后续工作中讨论。

3 结束语

基于振动速度和振动位移间的微积分关系，推导出了基于振动速度描述峰值位移的新方法。模拟结果表明，燃烧始点后到缸内峰值压力前的振动速度对峰值位移的提取影响最大。该阶段振动速度积分所得Smax和pmax为近似线性对应关系。试验结果表明，基于振动速度提取的Smax和pmax为近似线性关系。基于实测数据，拟合出了不同机型Smax和pmax的线性关系曲线，基于拟合线性关系可实现缸内峰值压力的定量评价，但不同机型Smax和pmax比例关系不同。