城市共享单车停放点选址研究——以深圳市高新园区为例

黄伊萍，杨 雯

(深圳大学管理学院，广东深圳518060)

0 引言

2016年，共享单车迅速普及，大量出现在城市街头。截至2017年1 月22 日，共有四家互联网自行车企业(摩拜、ofo、小蓝、小鸣)在深圳市运营，累积投放自行车约30 万辆[1]。相对于传统的有桩公共自行车系统，共享单车因随借随还、随停随走、自由方便的特点更受大众喜爱。无桩共享单车的面世打通了城市公共交通出行的最后一公里，极大地便利了市民的出行。但共享单车随意停放的优势，也成了运维管理的一大症结。

随着使用人数的增加，乱停放的问题日益凸显，给城市运营、社会治理带来了新的挑战[2]。乱停放的共享单车不仅影响市容，还阻碍行人和非机动车的正常通行。调度成本也成为共享单车运营中的最大成本。为了规范共享单车的停放，需要推进道路两侧共享单车停放区域的规划和建设[3]。对共享单车停放点进行合理选址，有利于引导市民规范有序地停放自行车，解决共享单车乱停放、调度成本高的问题。

共享单车停放点选址跟一般设施选址问题一样，其目的是确定一个或多个设施点能够满足一定的标准和需求。文献[4]针对工厂选址问题建立多目标规划模型，以最小化总成本及未被覆盖的需求点。除了成本和覆盖范围，文献[5]在海啸多发地带的公共设施选址问题里还考虑风险因素。文献[6]以成本、客户服务水平及客户响应水平为目标，对分销网络的选址问题进行了研究。

有关自行车停放点的研究多数聚焦于有桩公共自行车。文献[7]以巴黎市的公共自行车租赁系统为例，通过预测出行需求量来确定租赁点的规模，并且阐述了设置租赁点的影响因素、定位方法以及布设原则。一些学者采用定性与定量结合的方法(如层次分析法、模糊综合评价模型等)评估选择公共自行车租赁点[8-10]。由于公共自行车租赁点的选址具有较多的量化指标，如步行距离、建设成本等，因此很多学者采用定量方法进行研究。文献[11]通过建立双层规划模型以使出行成本和设施建设成本最小化，并用遗传算法求解模型，得到公共自行车租赁点的最优布局。文献[12]针对柳州市公共自行车租赁点选址现状、影响因素及主要问题进行分析，提出相应的解决办法，并运用基于集合覆盖方法的公共自行车租赁点选址模型进行案例分析。

对于覆盖选址问题，许多学者提出了不同的覆盖模型。传统的覆盖选址模型中需求点的覆盖只分为两种情况，要么在设施点服务半径内被视为完全覆盖，要么在设施点服务半径外被视为完全不覆盖。然而，设置严格覆盖半径并不切合实际情况，假设覆盖半径为100 m，在99.9～100.1 m 之间不一定会出现完全不同的覆盖情况。基于此，文献[13]最早提出了逐渐覆盖模型的概念，并描述了需求线性递减的逐渐覆盖模型。文献[14]提出非凸非凹的渐进覆盖模型来描述距离和覆盖水平之间的变化关系。文献[15]最早建立了基于服务质量的渐进覆盖模型，提出可接受的最小服务水平的概念和不同的覆盖函数。文献[16]从服务质量的视角出发，建立了最大化总覆盖、最大化最小覆盖和最小化未覆盖的服务需求水平的多目标逐渐覆盖模型。文献[17]建立了以总需求服务质量最大化为目标的体验店选址模型。基于渐进覆盖和服务质量的多目标选址模型中，使用者在覆盖距离内完全覆盖，服务质量可以得到保证，中间部分服务质量随着距离的增大而不断下降，当距离值超过某个范围以后完全不覆盖，服务质量变为零。因此渐进覆盖模型更贴近共享单车停放点选址的实际情况。

共享单车停放点选址问题与公共自行车租赁点选址问题不同，其特点是可以任意地点无桩停放，即不用考虑建桩数量。本文将基于渐进覆盖方法建立共享单车选址问题的0-1 混合整数规划选址模型，并以深圳市南山区高新园区为例，在实地调查的基础上，利用该模型为该区域共享单车停放点的布局提供科学依据。

1 共享单车停放点选址模型

在共享单车停放点布局优化问题中，一方面，要考虑用户满意度。共享单车作为公共交通的补充以及短距离出行的代步工具，其特点是可以任意地点无桩停放。如果设置固定的共享单车集中停放点，其服务质量的高低主要取决于用户出发地或目的地与停放点之间的距离，即用户获得服务需要消耗的时间。将用户出发地或目的地与停放点的距离转化反映为用户时间满意度，采用余弦分布时间满意度函数作为服务质量水平函数，建立基于服务质量的渐进覆盖模型，并以停放点的总体服务质量最大化为目标。另一方面，需要考虑设置停放点给运营部门带来的管理成本。随着停放点选址数量的增加，相应的管理成本(如调度成本)也随之提高，而运营部门是以成本最小化为目标。该问题包含了两种不同的目标，为多目标决策问题。因此，建立如下共享单车选址模型：

式中：Q为共享单车停放点的总体服务质量；A为共享单车停放点的选址数量/个；N为需求点集合；M为共享单车停放点集合；wi为需求点i的需求量/个；dij为需求点i到停放点j的距离/m；qij为停放点j对需求点i的服务质量；Capj为停放点j的规模容量/个；xj表示当在j∈M设停放点时为1，否则为0；yij表示当需求点i∈N由停放点j∈M提供服务时为1，否则为0。

其中，式(1)、式(2)是目标函数，表示停放点的总体服务质量最大化和选址数量最小；式(3)确保每个需求点都能被停放点满足；式(4)表明只有设立的停放点才能为需求点提供服务；式(5)保证每个需求点对应的停放点的规模容量之和能够满足其需求量；式(6)保证设立的所有共享单车停放点的总规模容量能够满足所有需求点的总需求量；式(7)、式(8)是0-1约束。

式(1)中的服务质量函数qij选取余弦分布时间满意度函数，见式(9)。该函数曲线是截取余弦函数曲线的π/2 到3π/2 的部分。该曲线在阈值-D1和----D2附近的服务质量变化较小，曲线中间部分的斜率较大，也说明了这个范围的服务质量变化较大。但距离值一旦超过某个范围以后，服务质量变为0，即该停放点不为需求点提供服务。

2 实例分析

以深圳市南山区高新园区为例，规划区域北至深南大道，南接白石路，西临科技南路，东抵沙河西路，面积约为0.56 km2。轨道交通1 号线在深南大道设有高新园站。该规划区主要为办公功能区，高新园区内共享单车的使用者多为上班族，用途主要是短距离通勤或者换乘公共汽车与地铁。

图1a是高新园区内共享单车集中停放需求点的分布情况。上班族由于赶时间，一般会选择将单车就近停放在人行道边和绿化带旁，影响到行人的通行和路面交通的安全。

通过实地收集、整理高峰期高新园区连续一周五个工作日共享单车的需求数量(见增强出版网络文件附表1①)，将需求数量的均值作为每个需求点的需求量wi(见表1)。

高新园区是开发比较成熟的区域，并不能在任意位置进行停放点选址。因此，该案例属于离散型选址问题。需要先结合实际情况，按照一定的原则方法选取备选停放点，然后再根据所选的停放点能否满足需求量以及停放点与需求点之间的距离远近，对共享单车停放点进行优化调整。

图1 高新园区共享单车需求点及停放点位置分布Fig.1 Distribution of bike sharing demand points and parking sites in High-Tech Park

表1 高新园共享单车各需求点的需求量Tab.1 Amount of bike sharing demand points in High-Tech Park辆

共享单车停放点的选址主要考虑以下原则[18]：1)停放点在办公楼、公共汽车站等区域内的出行起终点附近进行选取，尽可能减少停放点与自行车使用者出行OD点(出发地和目的地)之间的距离；2)停放点不能对附近的交通环境以及行人出行造成影响，尽量避免主干路、办公楼停车场入口与空闲面积较小的绿化带旁；3)停放点选址时还需要考虑土地的经济适用性，应该充分利用空闲的土地，尽量减少开发新土地的费用，节约土地资源；4)停放点应该根据规划区域的规模形态特点，以均匀分布的模式进行选择。

根据该备选停放点的选址原则，在高新园区内初选的共享单车停放点的分布情况如图1b所示。

共享单车停放点的规模和可容纳的自行车数量Capj如表2所示。对于有桩停放的公共自行车租赁点，使用者可以接受的步行距离上限一般为500 m，但是因为共享单车无桩停放的特点，使用者可容忍的距离范围有所减小。根据问卷调查统计，超过65%的使用者可以接受的停放点与出发地或目的地的距离仅为200 m。因此，在渐进覆盖模型中取D1=0 m，D2=200 m，此时，qij的计算值表现为0～1之间的值，并且测得共享单车停放需求点i与停放点j之间的步行距离dij(见表3)。

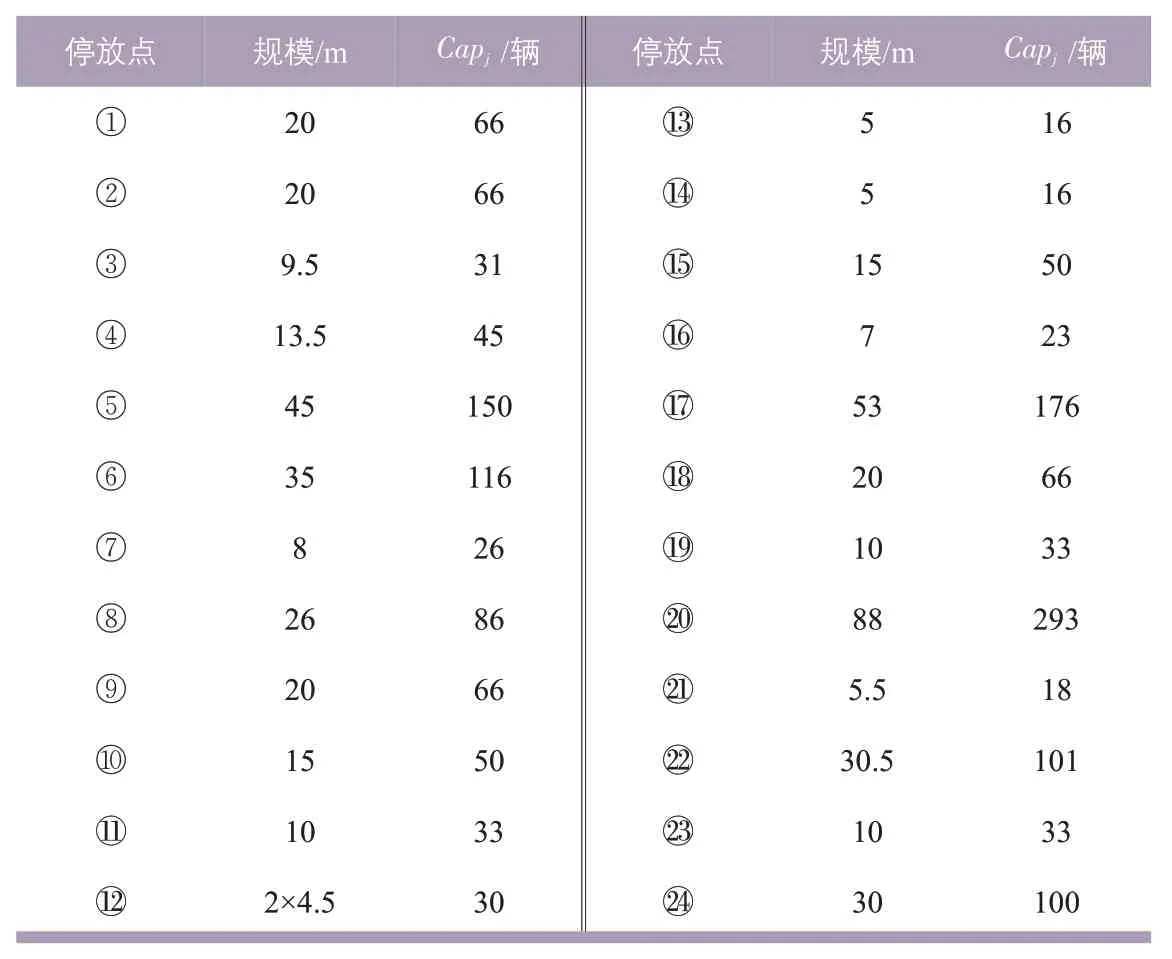
表2 共享单车停放点规模与容量Tab.2 Scale and capacity of bike sharing parking sites

3 问题求解及结果分析

为求解该多目标模型，将选址数量的目标函数式(2)转化为约束条件即改变最大停放点数量A，分析服务质量的变化。将上述调查得来的数据代入建立的选址模型，并利用LINGO 软件进行求解。当设定的选址数量上限A变化时，得到选择的停放点j(见表4)、目标函数值Q(见图2)，以及需求点与停放点之间的对应关系(i，j)都有所变化。

当选址数量上限A＜10 时，该模型无解，即当共享单车停放点小于10 个时，无法满足该区域内的出行需求。因此，求解结果中，将选址数量上限A从10 个依次增加到24 个，依次增加较优的选址停放点xj，当A=24 时，所有停放点都被选上。其中，需求点2与停放点②，⑧，需求点12与停放点⑥，⑦，需求点17 与停放点㉒，需求点18与停放点 ⑳ ，需求点20与停放点 ⑬ 之 间的距离都接近200 m的上限，即qij的值趋近于0。因此，需求点与停放点没有形成对应关系。

在目标函数中需求点的需求量作为权重影响着总体服务质量，因此用来满足需求量较少需求点的停放点不太容易被选上。由于高新园区的自行车使用者多数目的地是高新园地铁站，其中需求点6 离高新园地铁站步行距离仅350 m，这个需求点的需求量较少，因此停放点9在选址数量上限到达20个时才会被选上。同样，由于停放点1 和2 距离高新园地铁站约300 m，因此对应的需求数量为0，因此停放点1和2的增加对用户满意度几乎没有影响。该模型建议的选址结果与实际情况较为接近，具有现实意义。

由于选址数量越多，用户的时间满意度越高，但是会相应增加管理成本。据统计，每辆共享单车的调度成本为3元·辆-1·d-1，约300元可建设一个可以停放30辆共享单车的用于确定停车位置的电子围栏。根据以上成本信息，可以分析选址数量上限对时间满意度及管理成本的影响。

从图2 可以看出，随着选址数量上限的不断放松，用户的时间满意度随之增加，即共享单车停放点的总体服务水平不断增大。选址数量上限A从10 个依次增长到15 个时，满意度增加的速度较快；中间部分选址数量上限A大于15 个小于21 个时，满意度增加的速度放缓；当选址数量上限A增长到21 个及以上时，满意度增加的幅度极小。管理费用则随着停放点数量的增加成比例增加。因此，政府和企业可以根据实际情况，综合考虑总体服务质量与共享单车停放点的管理成本，设置一个合理的选址数量上限值，选取合适的停放点，以获取长久的效益。

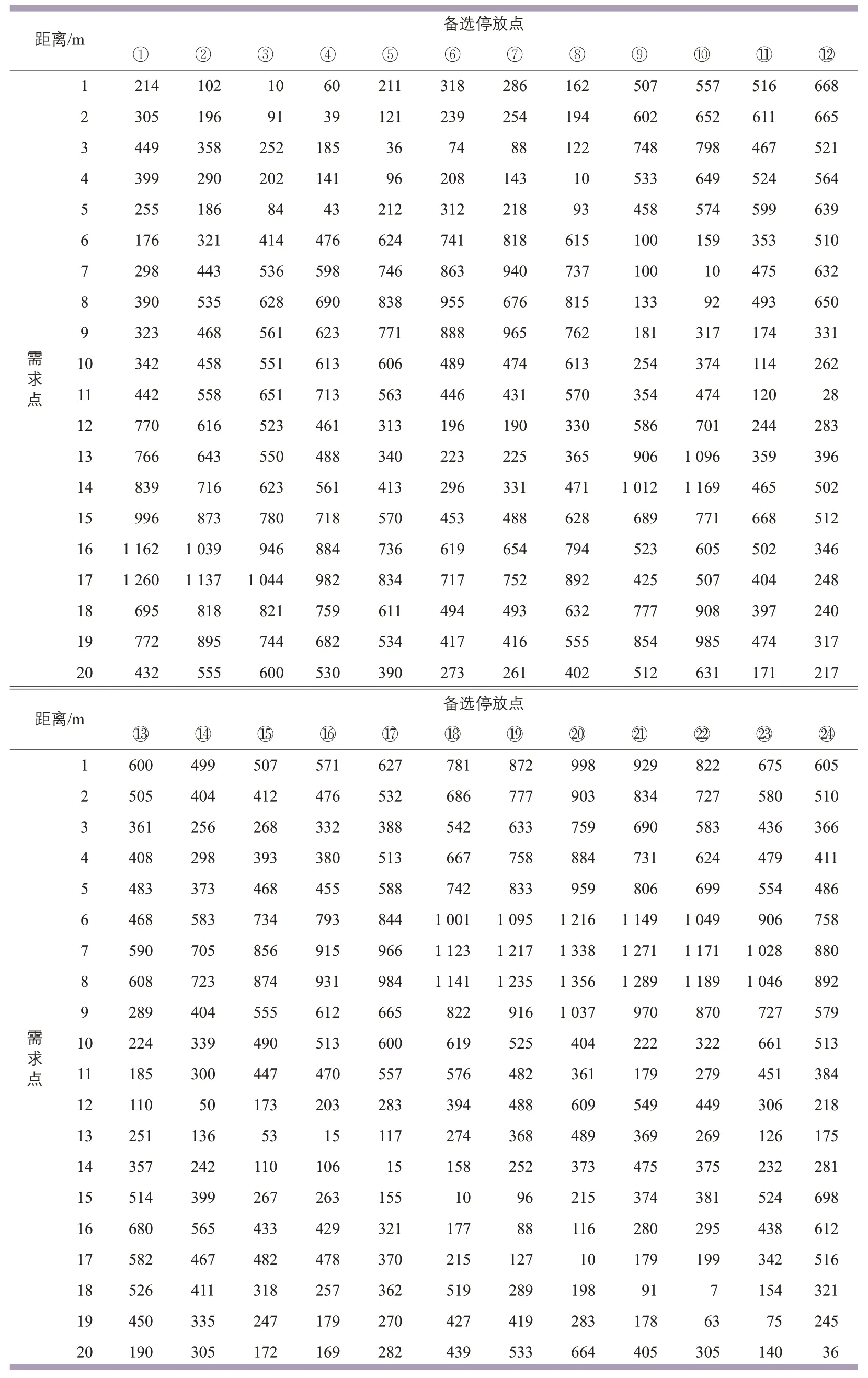
表3 共享单车停放需求点与备选停放点之间的距离Tab.3 Distance between demand points and parking sites

4 结语

本文在对深圳市高新园区出行调查数据分析的基础上，对城市共享单车停放点的选址进行了研究。考虑到需求点到停放点的距离对服务质量的影响，及停放点数目的增多带来的管理成本增加，结合更贴近实际情况的部分覆盖模型和余弦分布时间满意度函数，以停放点的总体服务质量最大化和选址数量最小为目标，建立基于渐进覆盖的多目标选址模型，采用LINGO 软件求解，得到建议的共享单车停放点。结果显示，采用文中所述模型建议的停放点选址结果与实际情况较为接近，具有一定的现实意义。对模型选址数量上限的敏感度分析，显示了最大选址数量对服务质量和管理成本的影响，可以帮助决策者根据实际情况在停放点管理成本和总体服务质量之间权衡，为共享单车选址提供参考。

表4 共享单车停放点 j 随选址数量上限A 的变化Tab.4 Change of bike sharing parking sites j with the upper limit of the location number A

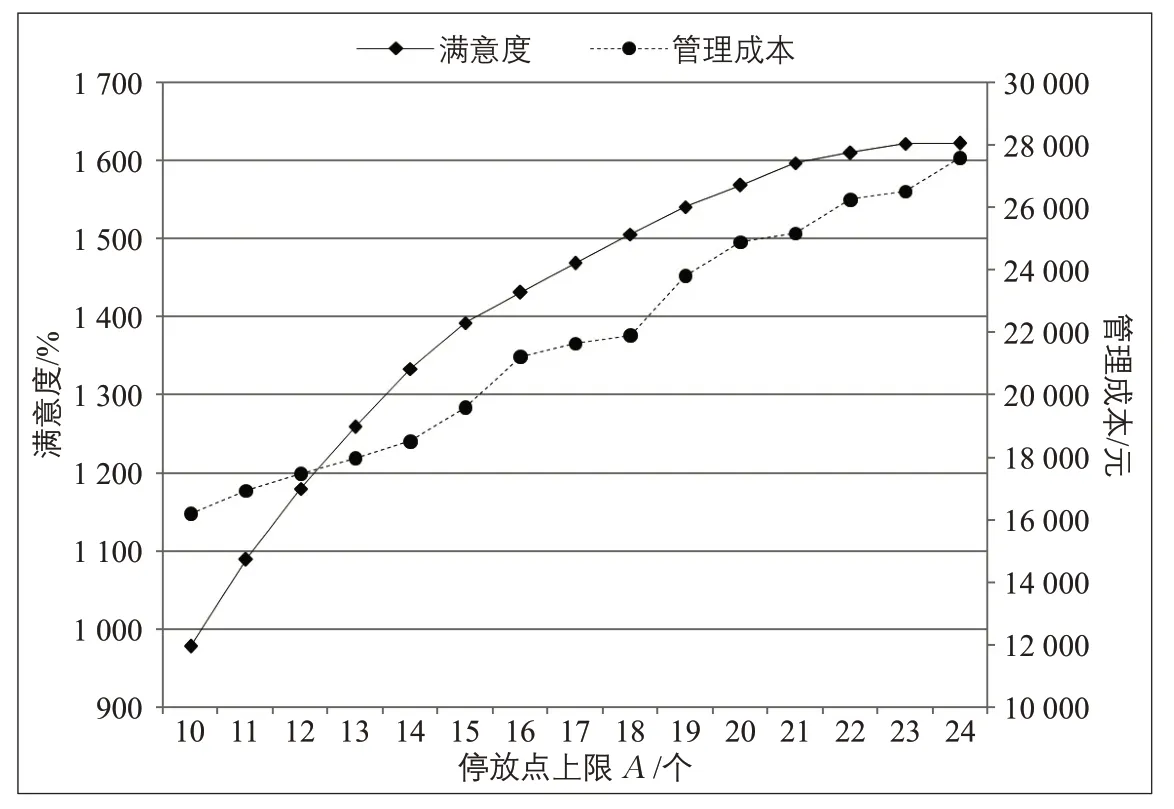
图2 选址数量上限变化对满意度和管理成本的影响Fig.2 Influence of different upper limit of the location number on the customers'satisfaction and administration cost

本文对于共享单车选址仍然有一些问题尚未解决，需要更全面深入的研究。如本文考虑的是确定需求，但在实际情况中，需求往往存在不确定性，需建立随机规划模型，模型求解变得更为复杂，但更有实际应用价值。

注释：

Notes：

①增强出版网络文件可在中国知网在线阅读。