高压线塔规划的物理解法

龚文鑫

（清华大学附属中学，北京 100084）

在我国基础建设日益蓬勃的今天，配套建设高压线塔等供电设施的需求也在不断扩大。本文以高压线塔的铺设为例，讨论如何在已知每一地点线塔造价（不同地理位置下的线塔架设难度不一）且路程足够远的情况下确定能使高压线塔总造价最小的线塔建造轨迹。由于单纯从各地线塔造价入手难以解决，文章通过借助费马原理转化，在线塔轨迹和几何光学三大定律之间建立联系，以便通过相对简单的数学计算和几何光学推论确定线塔架设轨迹。

1 模型建立

我们考虑的问题是在A 地和B 地建造一系列的高压线塔，并且总造价最少。在问题的考虑过程中，每一个线塔的造价成本与建造地点有关，记作n（x，y），相邻两线塔之间的距离始终不变，记作L，线塔数目记作N，则总费用p 为：

式中，ni为建造第i 个线塔所需成本。

由于相对实际路线长度，线塔之间的距离L 可以认为接近于0，所以在模型中，两地之间线路轨迹可看作平滑曲线，求和可以转化为积分。在转化的过程中将，由于L 很小且为定值，利用建设线塔过程中每一点铺设成本分布函数n（x，y）可以得知

2 使用光学方法求解模型

2.1 模型转化为光学问题

通过观察总费用p 的表达式，可以看出∫ ndl 和费马原理里面的光程表达式很类似。如果我们认为造价成本分布函数就是折射率，则光从点A 沿着实际的线塔设计路线射至点B，时长t 为

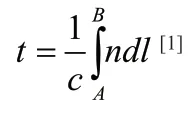
2.2 几何光学解法

由于费马原理和几何光学三大基本定律是相互等价的[1]，也即有：

（1）光线在均匀介质中沿直线传播。

（2）光的反射定律：光线在界面上的反射，入射角必须等于出射角。

（3）光的折射定律：n sin θ 为一个常数。

因此模型可以使用几何光学的三大基本定律求解，将结论代入模型，为满足总造价p 最小化，有如下推论：

（1）线塔在造价成本与建造地点无关的情况下应沿直线建造。

（2）在线塔规划路线中某区域不可建造（即费用无限大时）需要沿反射路径。

（3）在两造价不同区域相交时线塔路径满足n sin θ 是一个常数，其中θ 表示的是折射角，在模型中的含义是路径的切线方向和n（x，y）的等值面法线方向之间的夹角。

3 一个特殊情形

我们考虑在原点A（0，0）和终点B（xB，yB）之间的线塔造价分布函数n（x，y）以一次函数的形式递增，也即可以表达为函数n=ax+b（a，b 为常数且n>0恒成立）。

由于n sin θ 为定值，通过与文献[2]对比，可以得到实际光线轨迹方程：

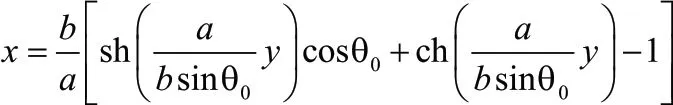
式中，θ0代表的是入射光线与x 轴正方向的夹角，也即入射光线的折射角。

由于轨迹经过B（xB，yB），所以需要满足可解得θ0，将θ0的结果重新代入可得轨迹方程。

我们画出a>0的轨迹方程的示意图，如图1。

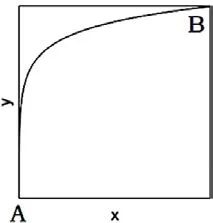
图1

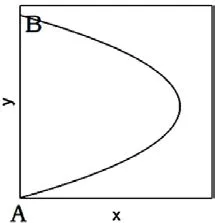
图2

可以看出，轨迹的斜率越来越小，这也和预期是一致的，因为此时的折射率随着x 的增加而增加，折射角θ 应该越来越小，而θ 角正是轨迹的切线方向和x 轴正方向的夹角。

我们画出a<0的轨迹方程的示意图，如图2。假设B 点的横坐标为0，则图示中的曲线只是一条备选轨迹，还有一条真实的光线为直线x=0，具体的轨迹选哪一条，还需要对比两条轨迹的工程造价，这是因为，在直线x=0的情形中，轨迹的长度较短，所造线塔的数目较少，而在图2所示的情形中，轨迹的长度较长，所造线塔的数目较多，但是每个线塔的造价会低一些。

这种情况可以推广到n 只和x 有关的情形，记作n（x），此时轨迹y（x）的导数为

式中，C 是待定系数。

求出该函数的原函数为

代入B 点坐标，使用y（xB）=yB能够求出来待定系数C 的取值，即可得到轨迹。

4 一般情形的讨论

一般情况下，我们设计的线塔路线规划有如下结论：

（1）如果轨迹经过造价特别大的地方，一定要以直线的方式快速通过，这是因为在该处n 特别大，此时θ≈0°，这也就意味着，该处的轨迹切线方向和该处的折射率等值面的法线方向是一致的，也就意味着轨迹在该区域内部的长度尽量小。

（2）如果轨迹经过造价特别小的地方，那么此时光线的n sin θ 值一定比较小，而经过该处时，θ≈90°，这也就意味着该处的轨迹切线方向和折射率等值面基本上相切，也就意味着轨迹在该区域的长度尽量长。

一般情形下的求解方案还可以转化为一个实验物理过程，设空间中各点的折射率由造价分布函数已知，现在由A 点出射一条光线，随着出射方向的改变，这条光线的轨迹也会发生改变，可以通过实验来看到光线随着出射方向的变化规律。在这些光线中，其中轨迹经过B 点的光线可能有若干条，因此可以作为备选的轨迹，在比较这些备选光线对应的造价p，取其中p 最小的光线即可得到问题的答案。

5 结束语

本文通过对路线规划问题建模，结合费马原理转化为了一个可求解的光学问题。需要注意的是，求解方案中光线的轨迹实际上取得是极值，而不是最小值[1，3]，所以该方法有一定的局限性。需要在实际计算中与另一条直线光路进行对比。本文详细介绍了线塔造价线性规律上升时的轨迹求解过程，同时提及了n 是一元函数时的推广情况。在几何光学基本定律的基础上可以通过诸多数学手段或者物理实验手段来寻找更广泛，更普适的高压线塔架设规律。希望日后能有更多拓展。