基于GaAs工艺L波段吸收式低通滤波器研制

文/马文涛 李宏军

从通信系统到射电天文，滤波器是必不可少的微波元件，几乎所有的微波接收机、发射机和微波试验装备都要求具有滤波的功能。常用的滤波器是反射式滤波器，是通过把不需要的频率成分的能量反射回信号源而达到滤波的目的，实现频率选择功能。

然而，某些场合却需要使用吸收式滤波器，将带外能量吸收掉。例如，吸收式滤波器用在大功率发射机上，以保护大功率管，使之避免由反射能量所引起的有害谐振。高增益的放大器在测试环境下绝对稳定，但在封装环境下带外信号会引起不必要的反馈，使得放大器变得不稳定，而吸收式滤波器的使用将避免此问题的发生。吸收式滤波器主要作用是将干扰信号，尤其是高频干扰信号的电磁能量转化为热能由吸收负载消耗掉，进而达到滤波效果。吸收式滤波器主要有两类：一类是从单端原型出发，以双工器或多工器的形式组合导纳曲线互补的不同滤波器来实现通带和阻带的全匹配。另一类是两个反射式滤波器与两个3dB 定向耦合器相组合，使阻带内反射的能量被耦合吸收。本文设计新型吸收式滤波器具有体积小、易与有源器件集成，一致性好等优点。

1 吸收式低通滤波器芯片的设计

本文采用奇模偶模理论分析得到吸收式滤波器的拓扑结构原型 ，对于一个对称的两端口网络，如果两个端口采用等幅同相的信号进行激励，称之为偶模激励。此时对称平面可视为理想导磁面，两端口网络关于该平面完全对称，可以对其任一半进行分析，图1为偶模激励形成的单端口网络，输入反射系数称为偶模反射系数，用Γe表示，即Γ1=Γe。

图1：偶模激励以及单端本征网络

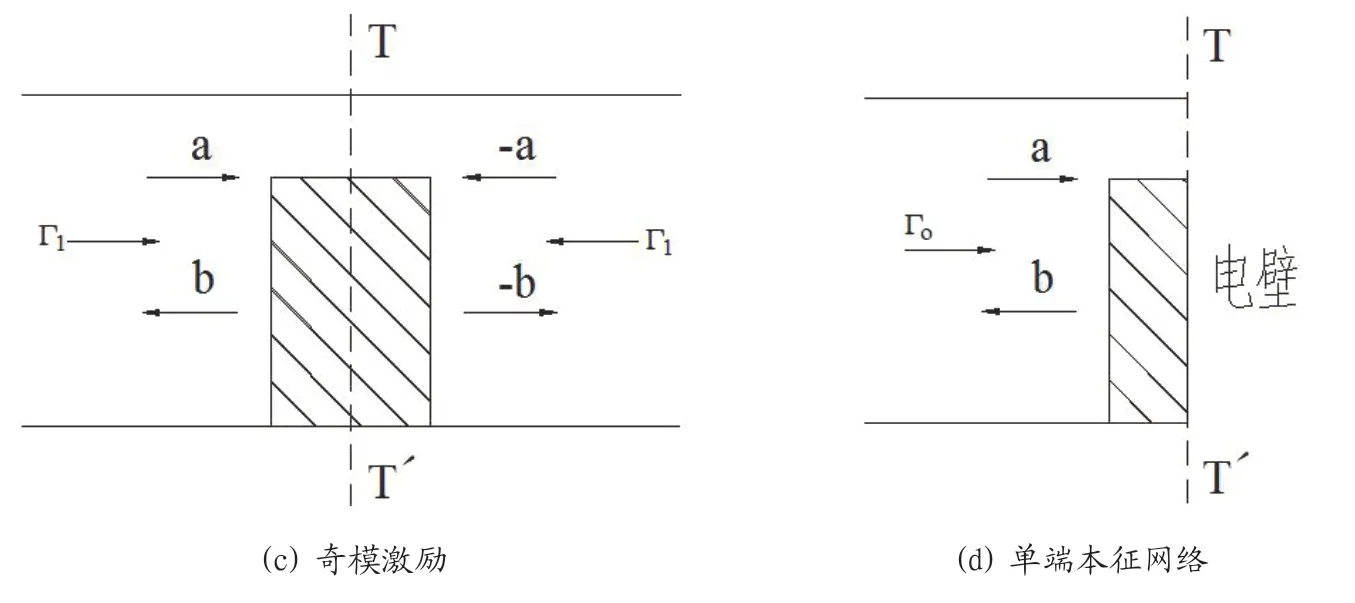
图2：奇模激励以及单端本征网络

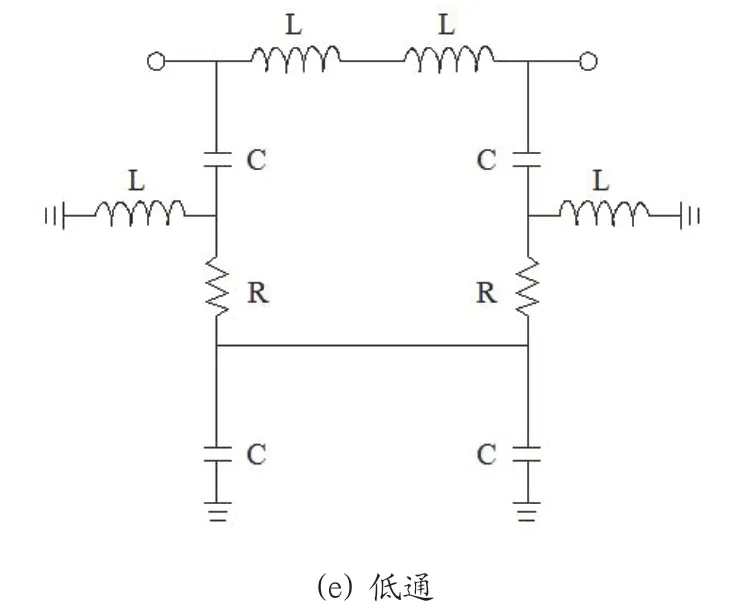
图3：单节吸收式滤波器拓扑图

反之两个端口采用等幅反相的信号进行激励称为奇模激励。此时对称平面可视为理想导电面，两端口网络关于该平面完全对称，同样可以取其中的一半来进行分析，如图2所示。对于奇模激励形成的单端口网络，输入反射系数称之为奇模反射系数，用Γ0表示，Γ1=Γ0。

所以，对称可逆二端口网络的散射矩阵可表示为：

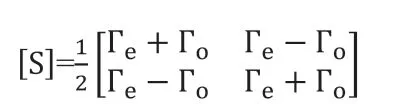
奇偶模分析的方法是通过把一个对称二端口网络分为两个单端口本征网络分析研究，求解本征值的方法，从而使得求解过程大为简化。

同理，可以采用上述方法，可以把对称网络的阻抗矩阵写为：

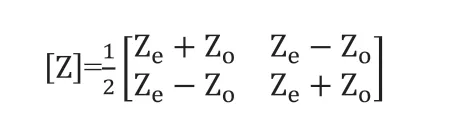
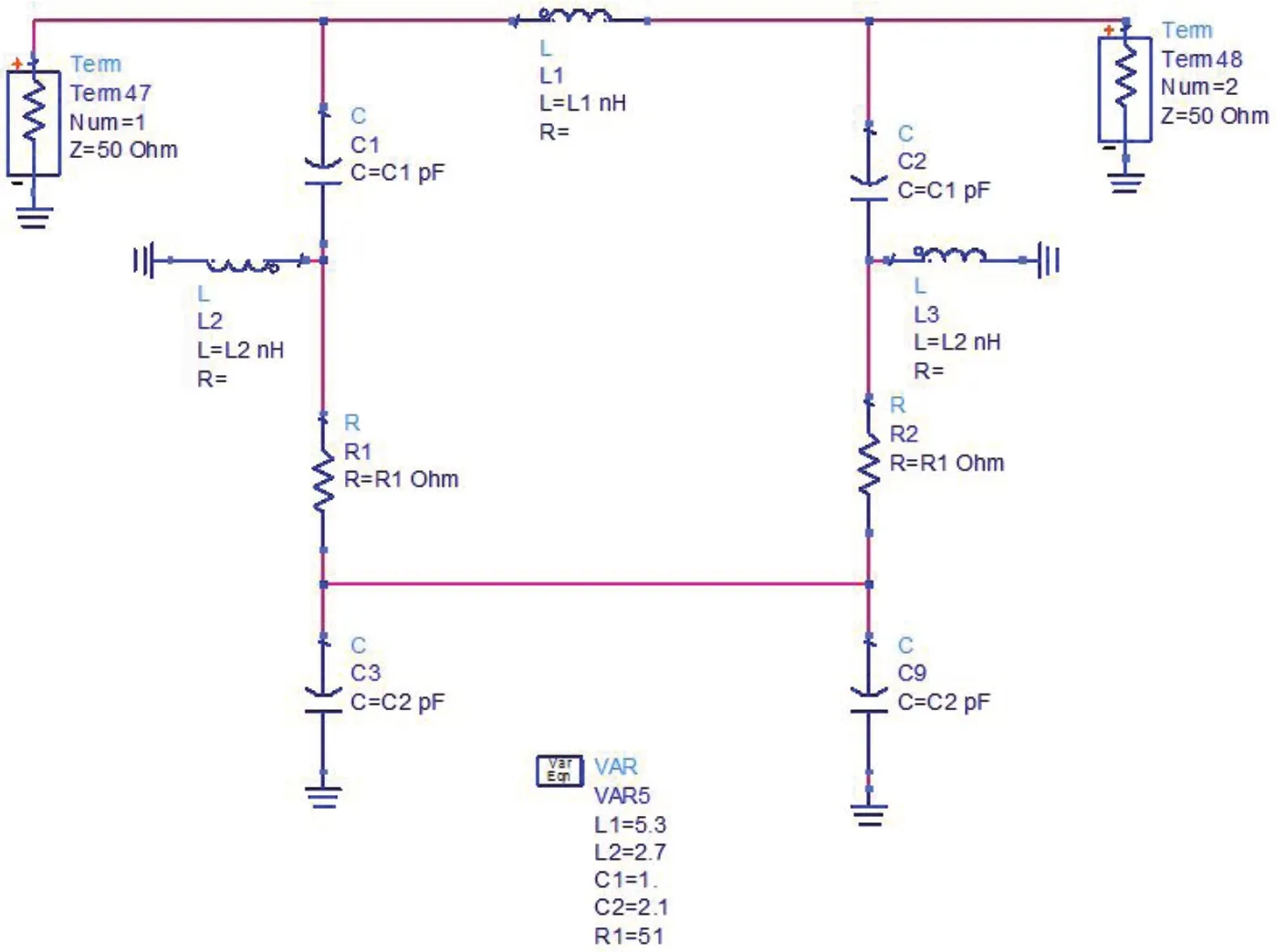
图4：单节吸收式滤波器电路结构

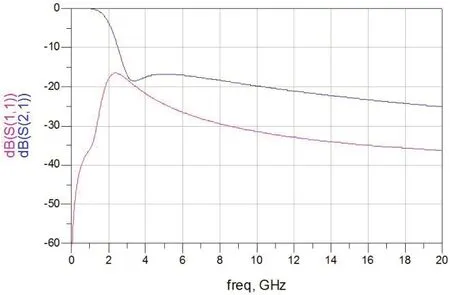
图5：单节吸收式滤波器仿真曲线

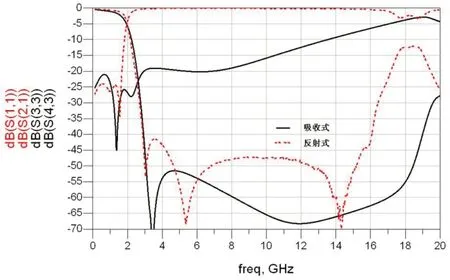
图6：吸收式滤波器与反射式滤波器幅频特性对比

图7：吸收式滤波器芯片照片(2.8mm×1mm×0.1mm)

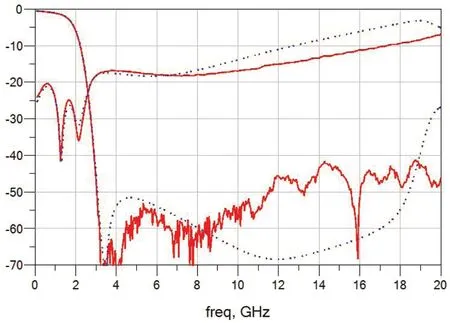
图8：吸收式滤波器仿真与测试曲线对比

式中Ze和Zo分别为偶模和奇模单端口本征网络的输入阻抗。Ze、Zo也即为终端开路和短路状态下单端口本征网络的输入阻抗。

通过上述分析，以及一系列的变换可以得到吸收式低通滤波器拓扑结构如图3所示。

2 吸收式低通滤波器芯片的实现

本文我们采用70um的GaAs工艺进行滤波器的设计，考虑到滤波器性能指标以及芯片尺寸等综合因素元件实际采用螺旋电感与薄膜电容来实现。通过合理设置滤波器元件的初值，然后通过优化完成最终的设计。

电路结构以及仿真曲线分别如图4、图5所示。

3 吸收式低通滤波器芯片的仿真与测试结果分析

如图6、图7和图8，由仿真和芯片测试曲线可以看到，在DC～10GHz频率范围内仿真与测试结果吻合较好，吸收式低通滤波器在DC～3G频率范围内电压驻波比小于1.2，12倍频抑制大于40dB，相比于普通的反射式滤波器，此吸收式低通滤波器在DC～12G的频率范围内驻波比小于2，同时远端寄生通带以及本底抑制均优于同频段反射式滤波器。

4 结论

本文简单介绍了吸收式滤波器基本理论以及分析方法，并设计了一款L波段的吸收式低通滤波器，设计结果证明了设计方案的可行性，同时也为吸收式滤波器的设计者们提供了一种可以参考借鉴的方案。