基于动态稀疏A*算法的广域无人机航路规划

文/黄文刚 陈奭

无人机（UAV）由于其人员零伤亡、高机动性、费用低等一系列优点，在军事和民事领域受到广泛关注。对于UAV的航路规划，国内外学者提出了很多方法，如A*算法、遗传算法、蚁群算法等。在众多算法中，A*算法由于其简单高效而得到广泛应用。但A*算法要收敛到最优解需要很长的时间和较大的运算资源，且生成的航迹并不一定满足UAV的机动约束条件。Szczerba等人于2000年提出在搜索算法中结合约束条件的稀疏A*算法，有效地缩短了计算时间。然而稀疏A*算法在复杂广域环境规划高质量的航路仍较为耗时，而现代战争，分秒必争，基于此，本文提出了针对复杂广域环境下的分层动态稀疏A*航路规划算法。

1 基于稀疏A*算法的航路规划

首先，航迹代价的计算公式描述为：

图1：当前节点的二维搜索区域

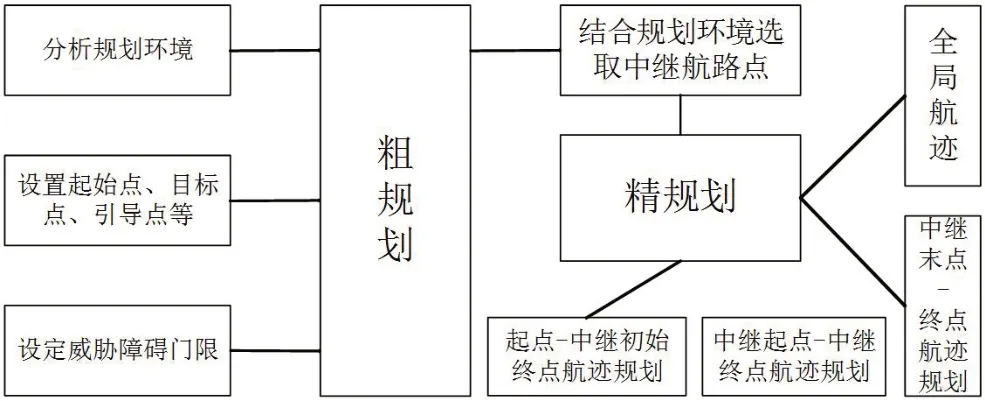
图2：分层算法架构

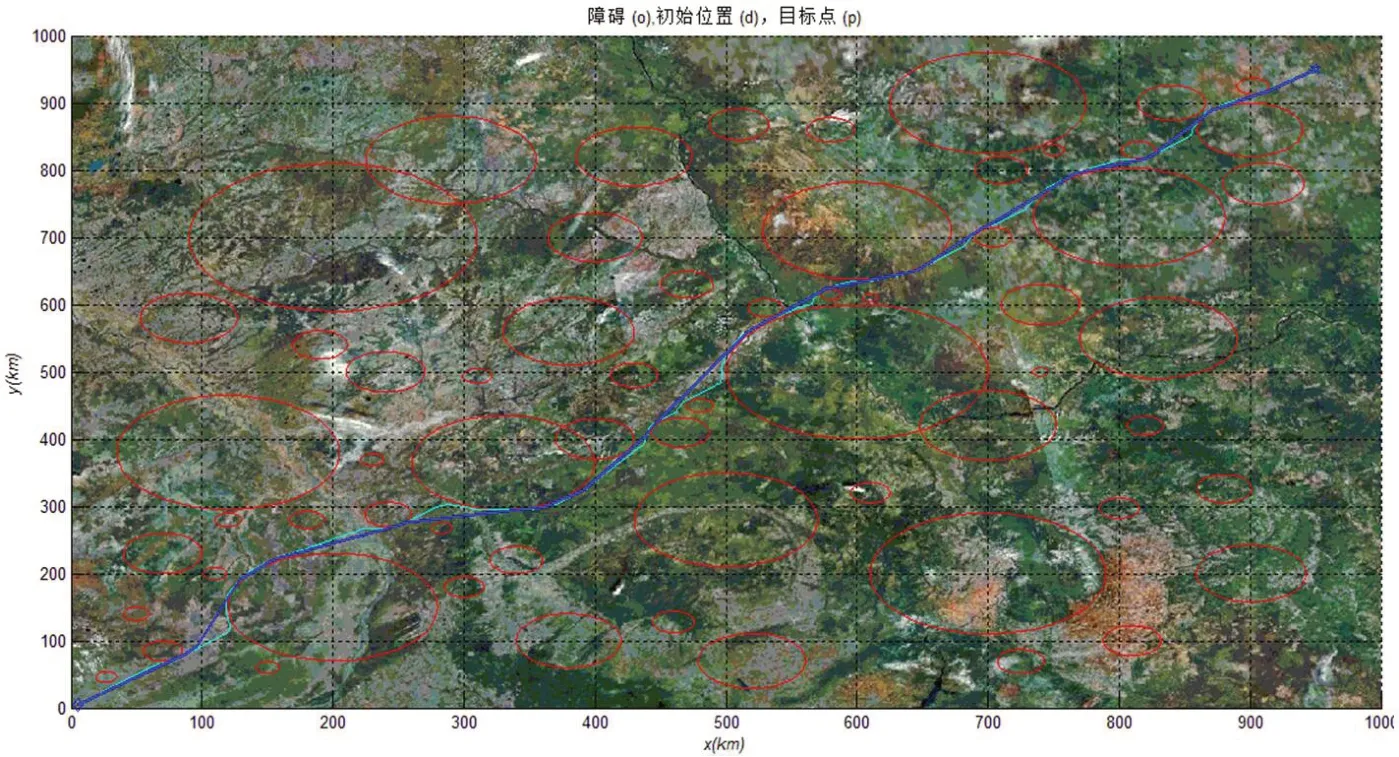
图3：广域动态稀疏A*算法航路规划

图4：分层方法粗规划航路

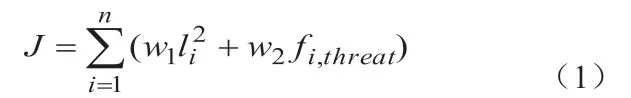
其中，J是航路规划的代价函数；n为总航迹段数；li表示第i段航迹的长度，通过约束航迹的总长度可缩短UAV的飞行时间，既节省了油耗，又降低了UAV的危险系数；fi,threat为第i段航迹的威胁指数，它限制UAV不要与已知的威胁障碍距离太近；w1、w2为权系数。

稀疏A*算法是标准的启发式搜索算法A*的改进。传统的A*算法进行航迹搜索时，通常将规划环境网格化，通过预先确定的代价函数（式（2））寻找最小代价航迹。

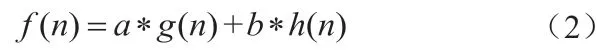
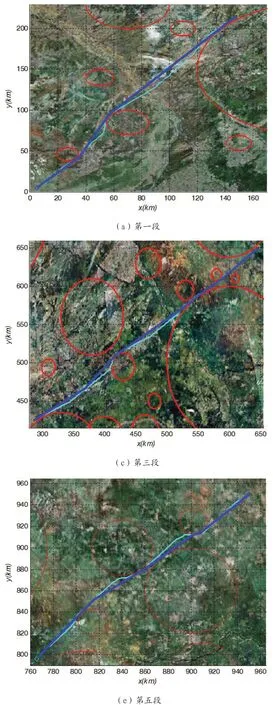
图5：分段小区域航路规划图

图6：分层航路规划全局航路图

其中，g(n)为从起始点到当前节点n的实际代价，启发函数h(n)表示从当前节点到目标点的估值，a、b代表真实代价和预计代价的加权。A*算法每一步的扩展中，具有最小f(n)值的节点被选择并插入可能路径OPEN链表中。

稀疏A*算法结合的约束条件主要包括最小搜索步长、最大转角、航迹距离约束和固定目标进入方向等。最小步长是无人机在改变姿态时必须直飞的距离，也是每次搜索的最小距离；最大转角约束生成航路的最大拐弯角。稀疏A*算法以扇形节点作为扩展节点，缩减了搜索区域和搜索时间。关于稀疏A*算法的详细表述可以参考文献[2]。

2 基于动态稀疏A*算法的航路规划

在无人机航路规划系统中，无人机安全有效地规避障碍物直至到达目标点，规划航路的搜索扩展方法是关键。在稀疏A*算法的基础上，结合飞行环境，通过定长的OPEN表、改进搜索扩展方法、二次优化等思想，给出了一种基于可行优先准则的航路规划方法，即动态稀疏A*算法，该算法极大地缩短空间搜索时间并减小搜索空间，同时保持较高航路飞行品质。

2.1 改进扩展规划区域

稀疏A*算法在节点扩展过程中，结合航路约束条件有效地减小了搜索空间，缩短了搜索时间。动态稀疏A*算法借用稀疏A*算法中的“稀疏化”思想，采用定长的OPEN表，减少长距离时间的时间消耗，但与此同时又借鉴变步长思想通过离散化其局部规划区域而进行了改进。给定约束条件θ（最大转角）和最大搜索步长Lmax和最小搜索步长Lmin，则离散化的当前搜索区域如图1所示。若由节点Pk-1扩展到当前扩展到节点Pk，以节点Pk点为圆点建立搜索区域为步长Lmax为半径，夹角大小为2θ的扇形区域，动态稀疏A*算法将扇形区域进行点阵式离散化，n等分2θ的扇面，m等分Lmax与Lmin之间的距离，可以建立起(n+1)•m的待扩展点阵B。一般应根据规划环境选取合适的Lmax与Lmin。而m，n的值越大，找到满足要求的航路的概率就越大，但同时内存要求和收敛时间也相应增加。

搜索过程中并不需要遍历扇形区域内的每一个位置，而只需考虑其中的离散化点阵节点，依据上图中给出的搜索方法，由Pk点至第Pk+1点可扩展点Bi,j的坐标(xk+1,yk+1)计算如下：

其中，：

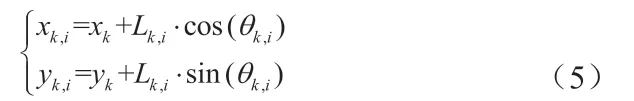
相比稀疏A*算法的搜索区域，动态稀疏A*算法因其离散化处理故可以选取较大的局部搜索区域，克服了搜索区域大小和地图分辨精度之间的矛盾，且规划时间短。

2.2 基于二次优化的航迹优化

初始航路点生成之后，在满足飞机机动性能下，采取二次优化算法进行航路优化，优化的航路可有效缩短曲折路径，减少了飞机动力消耗，缩短了飞行时间；该二次优化算法也可用于地面无人车、无人机船等规划路径的优化。

3 分层动态稀疏A*算法

分层动态稀疏A*算法采用分层思想处理不同环境约束，分割规划环境，先后对分层区域进行航路规划，相比单一的动态稀疏A*算法优势在于面对较大的较为复杂的规划环境时，分层稀疏A*算法能够更加快速规划出高质量的飞行航路。分层算法框架结构如图2所示，首先分析规划环境，明确无人机任务的起始点、目标点、任务引导点、安全区、匹配区，以及规划空间中的地形、敌方雷达、禁飞区等威胁；然后通过计算将相交连的中小威胁合并为一个整体，确定整体的威胁范围；设置合理的威胁范围门限，忽略作用范围小于门限的威胁，结合搜索环境确定合适的步长，在含有大范围威胁的环境中进行粗航路规划；然后选取中继航路点，分割规划环境，在小范围内加载所有威胁障碍信息后进行精细航路规划，最后顺序连接每段小范围内规划的航路得到整个大范围的完整航路。分层规划是一种处理大范围任务区域的思想，具体的粗细规划也可采用其他算法。

中继航路点可以通过算法自动选取，将第一层粗规划的航路按一定航迹长度划分，划分间隔位置选为中继航路点。简单方便起见也可以选取一些距理想航路较远的粗规划航路点作为中继航路点。

4 仿真结果

分层稀疏A*算法在Pentium(R) Dual-Core 2.6GHz PC机上进行了仿真实验，运行环境为Windows XP，编程环境为matlabR2011b。广域任务规划区域见图3。基本仿真参数设定为：任务区域为1000km×1000km的正方形区域；航路起点start=[5,5]，目标点target=[950,950]；威胁源用图中红色圆形区域表示，圆形区域之内为不可飞行区域；代价函数中系数，w1=w2=1/2；在进行节点扩展时，N=4；最大转角θ=45°；

在仿真中，设计了采用同分层算法的精细规划中步长相同的动态稀疏A*算法进行航路规划，作为对比。如图3所示，算法中选取最小步长L0=2km，大步长L=2L0，算法规划初始航迹如图中青色线，优化后如蓝色实线。算法规划的航迹长1396.3403km，耗时6.3715s。

图4为分层算法中基于动态稀疏A*算法的粗规划航路，算法中选取最小步长L0=10km，大步长L=2L0，选取威胁门限为45km，即在粗规划中整体威胁半径小于45km的威胁被忽略。粗规划稀疏A*算法规划初始航迹如图中青色虚线，优化后如蓝色实线，规划耗时0.6819s。结合粗规划航路和全局环境选取中继航路点(a)(148.4605,216.3442)、(b)(286.1584,424.8660)、(c)(647.9430,651.3517)、(d)(766.0722,796.5406)，从起点向终点方向依次如图中绿色星号。

图5中（a）～（e）为按起点到终点方向次序的小区域的航路规划图。算法中选取最小步长L0=2km，大步长L=2L0，精细规划稀疏A*算法规划初始航迹如图中青色虚线，优化后如蓝色实线，优化后航迹长度，图（a）256.9741km，图（b）250.2602km，图（c）428.3721km，图（d）187.2797km，图（e）241.4205km，耗时分别为0.6685s、0.6612s、0.9106s、0.5614s、0.6521s。

图6为采用分层规划算法规划的全局航路图，图中蓝色航路为图5中5个子图各自规划后的优化航路依次衔接而成，全长1364.3066km。分层算法耗时为粗规划时间加所有子图的规划时间，即3.2251s。如果几个子图采取并行规划，则分层算法耗时 粗规划时间+max（子图（a）～子图（e）规划时间）。

5 结束语

通过仿真图与数据可以看出，相比直接进行广域规划，基于分层动态稀疏A*算法的航路规划既保持规划精度又缩短了规划时间，精细规划中每个小区域相对独立，可以结合各自环境选取合适的算法进行规划，且可以借助多处理器进行并行规划。分层动态稀疏A*算法耗时更少，规划航迹更短，飞行品质更优。