基于多维缩放和随机森林的轴承故障诊断方法

张西宁,张雯雯,周融通,余迪

(西安交通大学机械制造系统工程国家重点实验室,710049,西安)

滚动轴承是极为重要的机械基础件,因其高效率、便于装配以及易润滑等优势,广泛应用于国民经济和国防事业各个领域[1]。作为旋转机械中的关键零部件之一,滚动轴承运行状态直接关系到机械设备的性能和使用寿命。然而,滚动轴承是机器中最易损坏的元件之一[2],据不完全统计,旋转机械的故障约有30%是由滚动轴承引起的。因此,滚动轴承的故障监测诊断技术成为国内外的研究重点。

目前,对于滚动轴承的智能诊断大多数针对其振动信号,提取时域、频域、时频域中的幅值谱、幅频图、功率谱、小波能谱、希尔伯特边际谱等谱图参数组成特征向量[3-6],或者利用样本熵、模糊熵、幅值谱熵等信号处理方法构造特征集[7-8],然后通过模式识别的方法进行故障诊断。大量不同的机器学习算法,如支持向量机、人工神经网络、决策树、逻辑回归等,被广泛应用于构建分类器。单一特征向量在不同数据集中的表现差异造成了提取多种特征的必要性。然而,特征向量维数的增加不一定能提高诊断准确率,这就对有效信息的综合提取和无用信息的摒弃提出了要求。

在高维情形下,所有机器学习方法均会面临样本稀疏、计算困难等形式的“维数灾难”[9],此时往往通过特征融合或特征选择对高维特征集进行降维。多维缩放是一种经典的降维方法,它维持了降维前后样本之间的距离不变,将原始数据“拟合”到一个低维坐标系中,使得由降维所引起的任何变形最小。

本文提出基于多维缩放和随机森林的轴承故障诊断方法,采用函数型数据分析中的基函数展开法,提取的滚动轴承振动信号自相关函数的函数拟合系数作为状态特征,对比了特征选择对特征提取的影响,并使用多维缩放对特征集进行了降维,结合随机森林模型,实现了对滚动轴承的故障诊断。

1 基础理论

1.1 函数型数据分析

对于随时间变化表现出函数特征的数据,函数型数据分析(FDA)回归到数据产生的本质,将其转化回函数,并进行进一步分析[10]。它以“化数为形”为基础思想,将收集到的样本数据当作整体而非单个数值组成的集合。工程实际中,采集到的样本数据通常是离散的、有限的,因此在FDA中用基函数展开法将原始离散振动数据转换为一个光滑的函数。

滚动轴承不同元件缺陷产生的振动信号,表现为滚动体在滚道上的通过频率或者滚动体自转频率对外环固有频率的调制现象[11]。旋转机械正常运转时,振动数据曲线一般为三角函数形式,傅里叶基函数就可以满足其函数型转换需求。假设内圈存在一个缺陷,当轴转动时,这个缺陷与滚子产生的振动会不断改变,采集到的数据会有内圈转动产生的调幅影响。假设滚动体存在一个缺陷,当轴转动时,这个缺陷与滚道产生的振动会不断改变,采集到的数据会有滚子转动产生的调幅影响。假设外圈存在一个缺陷,由于外圈通常保持不动,且加速度计安装在外圈正上方,这个缺陷与滚子产生的振动位置不会改变,滚子的振动不会对其产生调幅影响。

不同状态下的振动信号由于包含了不同成分会表现出不同的函数特征,振动信号与目标基函数的拟合系数在数值和相关性上不同。将函数型数据分析应用在故障诊断中的流程如图1所示。将清洗后的数据与设定的目标基函数进行拟合,拟合系数或误差参数可以作为样本特征用于训练分类模型。

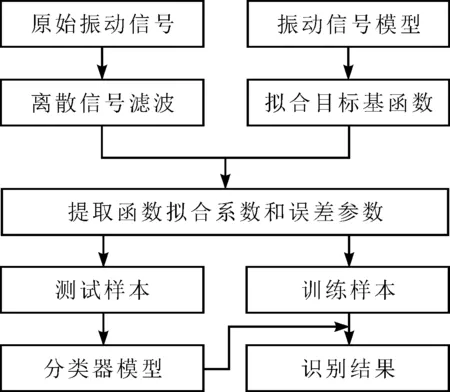
图1 采用函数型数据分析的故障诊断流程

1.2 多维缩放

通过降维方法缓解维数灾难是指通过某种数学变换将原始高维属性空间转变为一个低维子空间,以提高样本密度并简化计算。目前常用的线性降维方法如主成分分析、线性判别分析;非线性降维方法如局部线性嵌入、拉普拉斯映射等流形学习方法。主成分分析[4](PCA)通过正交变换将原始特征转换为线性独立的特征,使投影后样本点的方差最大化,但是贡献率小的主成分也可能包含对样本差异的重要信息。t分布随机邻域嵌入(TSNE)[12]基于样本点之间的分布概率不变,将距离大的簇之间的距离拉大,解决了随机邻域嵌入(SNE)的拥挤问题,但是TSNE在样本较多时构建困难、梯度下降慢。

多维缩放(MDS)要求原始空间中样本之间的距离在低维空间中得以保持[13]。假定m个样本在原始空间的距离矩阵为D,D的元素dij表示第i个样本和第j个样本之间的距离。MDS的目标是获得样本在d′维空间的表示Z,且任意两个样本在d′维空间中的欧氏距离等于原始空间中的距离。令内积矩阵B=ZTZ,作如下定义

(1)

(2)

(3)

MDS的算法流程见图2。该算法通过原始空间中的距离平方矩阵推导出降维后的内积矩阵,从而获得低维空间中的样本表示。

图2 多维缩放算法流程

1.3 随机森林

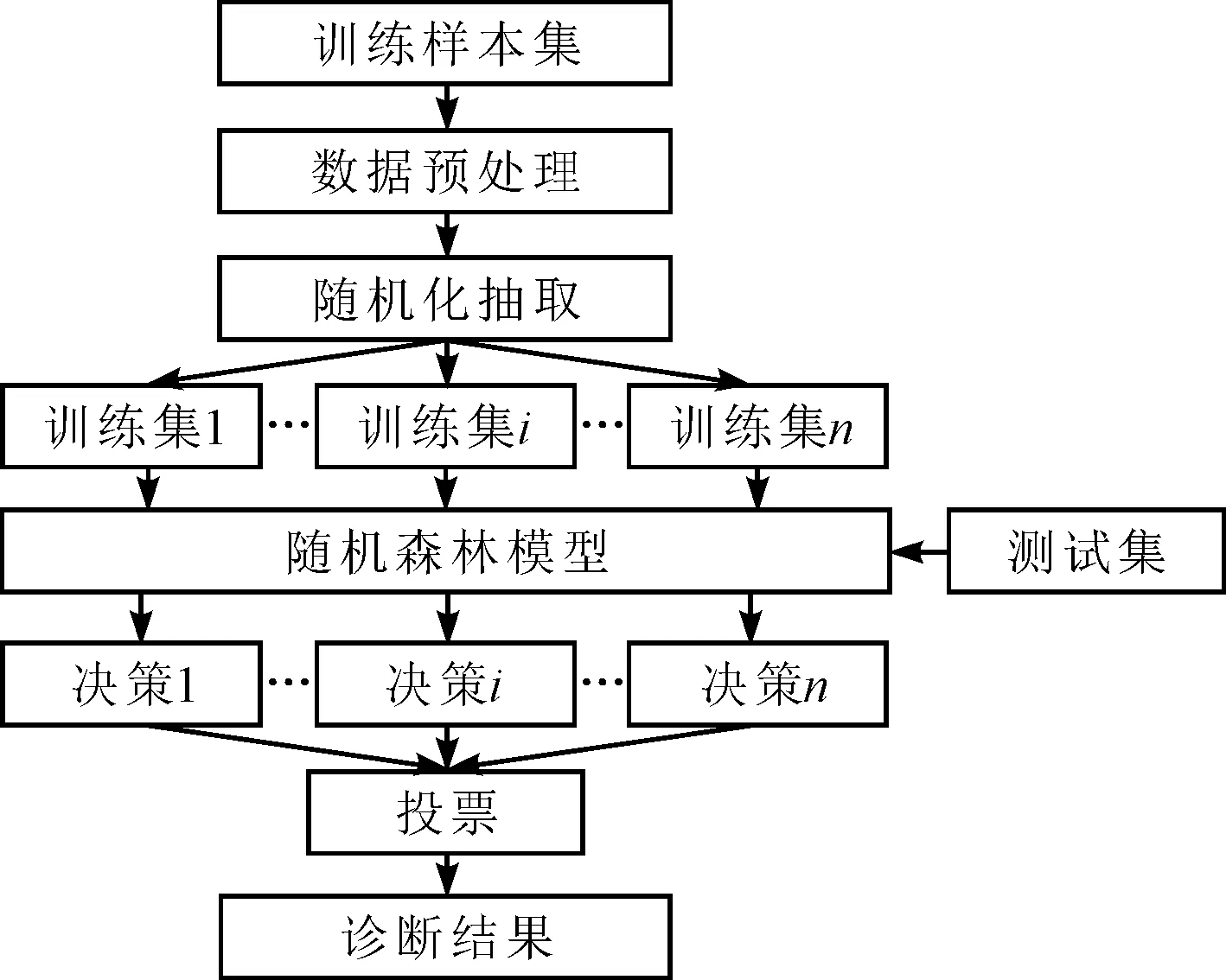
图3 随机森林诊断流程图

随机森林(RF)是以决策树为基学习器的装袋集成,在决策树的训练过程中引入了随机属性选择,每棵树生成时,训练集的抽取过程与节点分裂时特征属性的选择过程中的随机性,导致了采样的差异性和特征选取的差异性,从而大大提升了决策准确率[14-16]。分类模型输出结果由多棵决策树投票表决,少数服从多数。利用随机森林模型进行故障诊断的流程见图3。随机森林克服了决策树容易过拟合的问题,对噪声和异常值有较好的容忍性,对高维数据分类问题具有良好的可扩展性和并行性,给出的特征重要性排序是验证初始假设和评价模型学习效果的好方法[17-18]。

2 轴承故障诊断方法

根据上述分析,本文提出了基于MDS和RF的滚动轴承故障诊断方法。该方法流程如图4所示,具体步骤如下:

(1)对轴承振动信号的自相关函数做函数型数据分析,取其拟合系数作为样本特征构造特征集;

(2)训练随机森林模型用于故障状态的分类,若训练误差与验证误差均在允许范围内,则进行测试,运行第(6)步,否则对模型进行优化;

(3)使用网格搜索法确定合适的基分类器数量与特征数量,并依据特征重要性排序做特征选择;

(4)使用MDS对特征集进行维数约简;

(5)训练得到最佳的随机森林故障诊断模型;

(6)对待诊断信号进行相同的取自相关、FDA拟合操作后,将得到的特征输入到训练好的随机森林诊断模型中,模型输出类别即为轴承状态类型。

图4 基于MDS和RF的轴承诊断方法流程图

3 轴承故障诊断实验

3.1 实验台及实验设置

本文构建了如图5所示的实验平台,包括直流驱动电机、支架、安装座、预紧装置、滚动轴承、传感器、电荷放大器、数据采集卡UA300等部分。轴承安装座的振动由压电型加速度传感器测量,灵敏度为8.8 pC/(m·s-2),频率测量范围为0.27～10 kHz。主轴键相信号由灵敏度为8×10-3V/μm的电涡流传感器测量。

图5 滚动轴承实验台

实验所用轴承均为6308深沟球轴承,有正常、内圈故障、外圈故障、滚子故障共4种状态。实验转速为1 200 r/min,径向加载7.7 kg的重物,采样频率为10 240 Hz,采样时间为20 s。采集到的信号如图6所示。

3.2 特征集构造

实验采集到的轴承振动信号包含了转频、倍频、故障特征频率、固有频率、噪声频率等非常复杂的成分。在对比了移动平均滤波、中值滤波、小波滤波3种常用方法的滤波效果之后,选择“db3”小波滤波作为预处理方法。

(a)正常信号

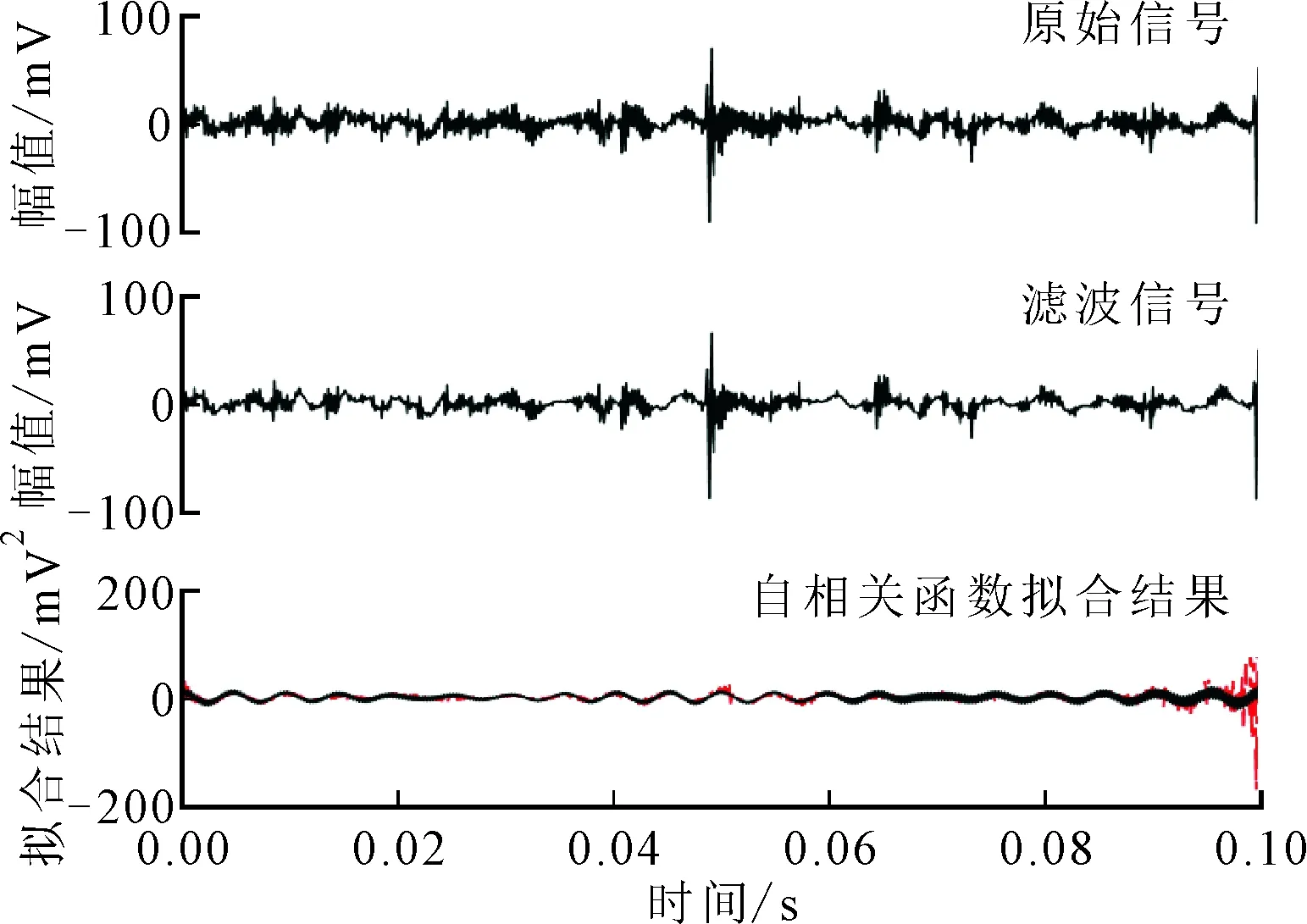
(b)内圈故障信号

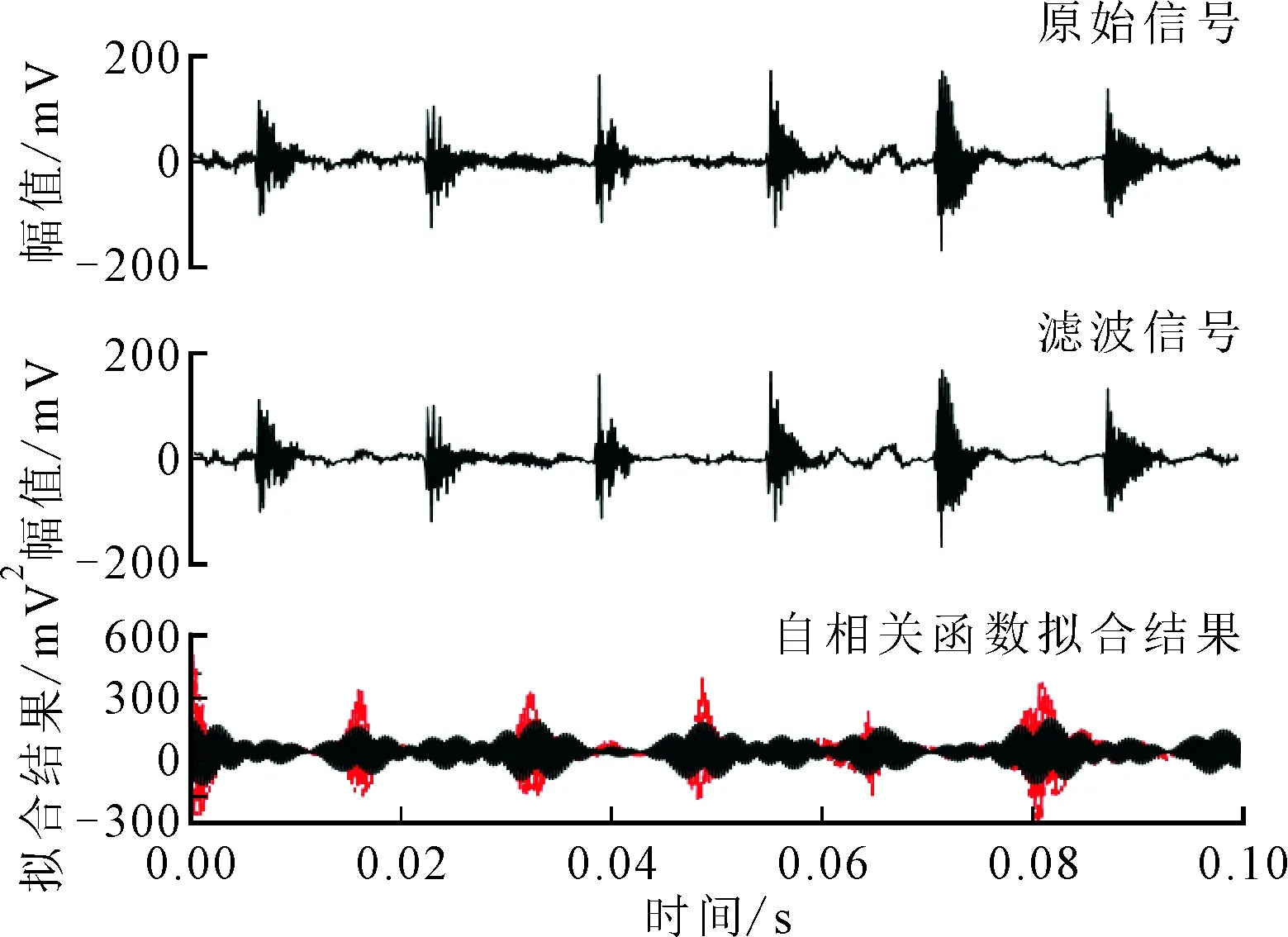
(c)外圈故障信号

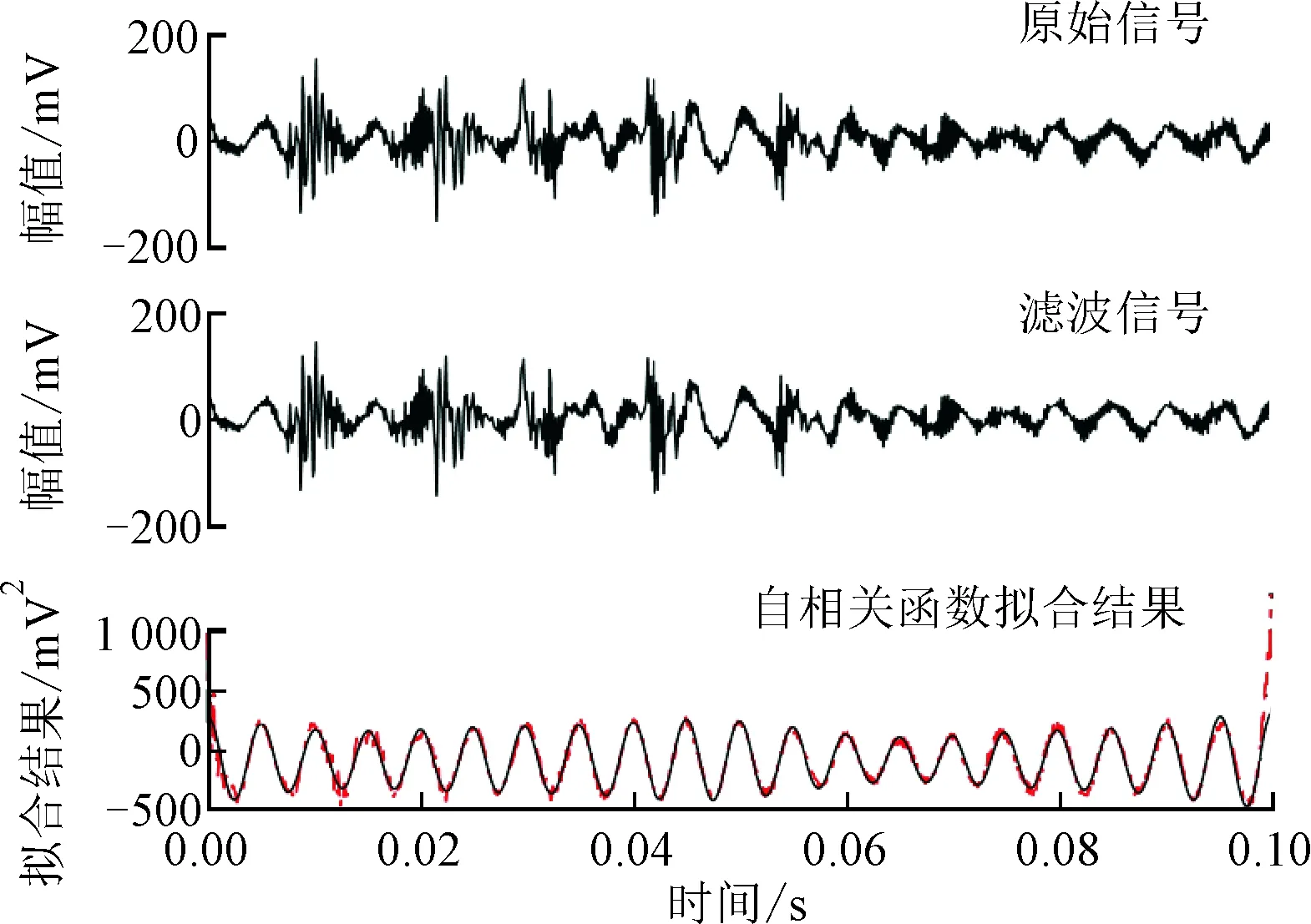
(d)滚子故障信号图6 轴承振动信号的FDA特征提取

振动模型的精确度和运算量使得即使对滤波之后的信号进行准确地函数拟合也是极其困难的,因此对振动信号的自相关函数进行了拟合。自相关函数含有与原振动信号同周期的成分,是从干扰噪声中找出周期信号或瞬时信号的重要手段。从图6中可以看出,对应4种状态的原始信号呈现出不同的特征,自相关信号也各不相同。

对各自相关函数用下式拟合

y(x)=a1sin(b1x+c1)+…+a5sin(b5x+c5)

(4)

得到的拟合系数ai、bi、ci(i=1,…,5)即为样本特征。从每种状态的20 s信号中截取了100段0.1 s的信号提取特征,每个样本特征有15维。4种状态的样本构成了大小为400×15的特征集,其中20%的样本用作测试集。

3.3 模型参数优化及特征重要性排序

随机森林往往使用默认参数可以得到不错的结果,其调参过程通常是对决策树个数ntrees和每棵树分裂时选用的最大特征数nfea进行的[15]。网格搜索法通过遍历已定义参数的列表来评估算法的参数,从而找到最优值,该方法适用于3个以及更少的超参数。

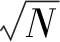
图7 随机森林参数优化结果

随机森林可以对变量进行特征重要性排序,其原理是逐次对每个特征加噪,观察对结果正确率或基尼指数的影响[16]。特征加噪后平均准确率减少得越多(影响越大),说明该特征重要;减少得越少(影响越小),说明该特征不重要。

对提取出的15个特征进行重要性排序后得到图8所示结果。由图8可见,c1、c5、c4、c2、c3对模型结果影响最小且与其他特征差距明显,因此除去这5维特征在一定程度上可以提高准确率。

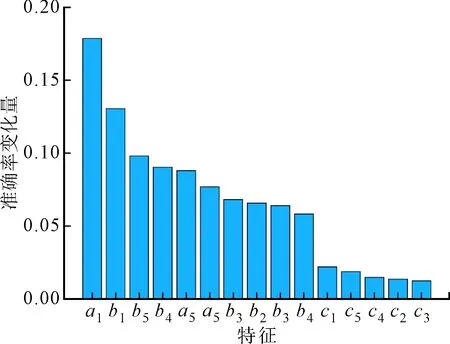
图8 特征重要性排序

3.4 维数约简

本文将TSNE和PCA两种降维方法与MDS的降维效果进行对比,降维前的特征被分为特征选择前后两种类型。为便于可视化,原始特征均降至二维,4种轴承状态的数据对应4种不同点的类型。降维后特征集由400×15减小为400×2。

降维后的数据首先进行归一化,然后用类内散布矩阵的迹表示类内距,用类间散布矩阵的迹表示类间距。我们希望降维后数据分布类间距大而类内距小,因此类间距与类内距的比值越大越好。3种方法的降维效果衡量见表1。

表1 3种方法降维效果衡量

图9显示对原始15维特征的降维效果,类间距TSNE最大、MDS次之、PCA最小;类内距MDS最小、PCA次之、TSNE最大。因此,类间距与类内距之比MDS最大、TSNE次之、PCA最小。图10显示了特征选择后10维特征的降维效果,其中距离大小分布排序与图9相同,但是特征选择后,MDS和TSNE的类间距增大,MDS的类内距略增大,TSNE的类内距增大较多,PCA的类内距与类间距均未变化。综合来看,特征选择使MDS的降维效果明显提升,使TSNE的降维效果轻微提升,对PCA的降维效果几乎没影响。

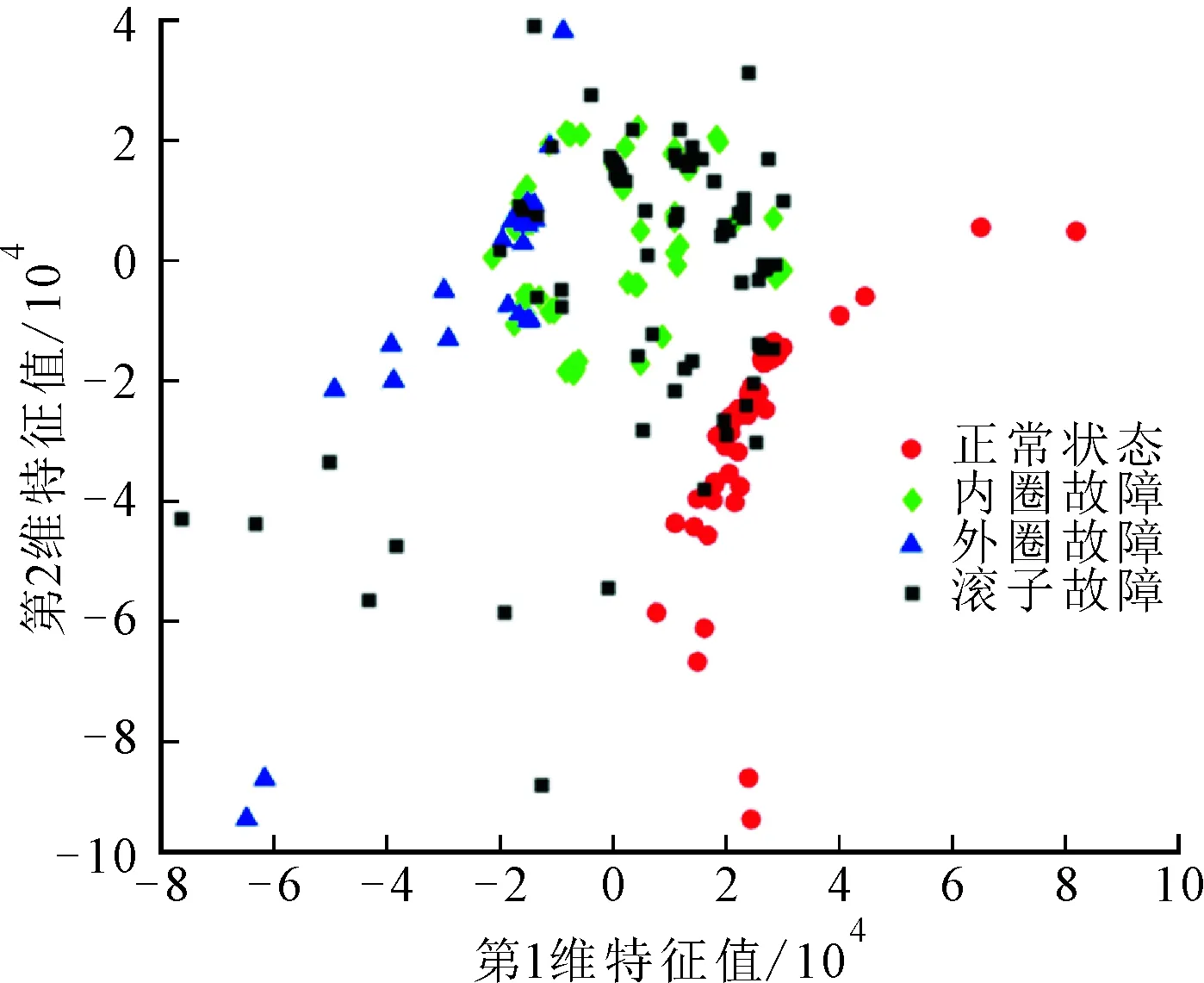
(a)MDS

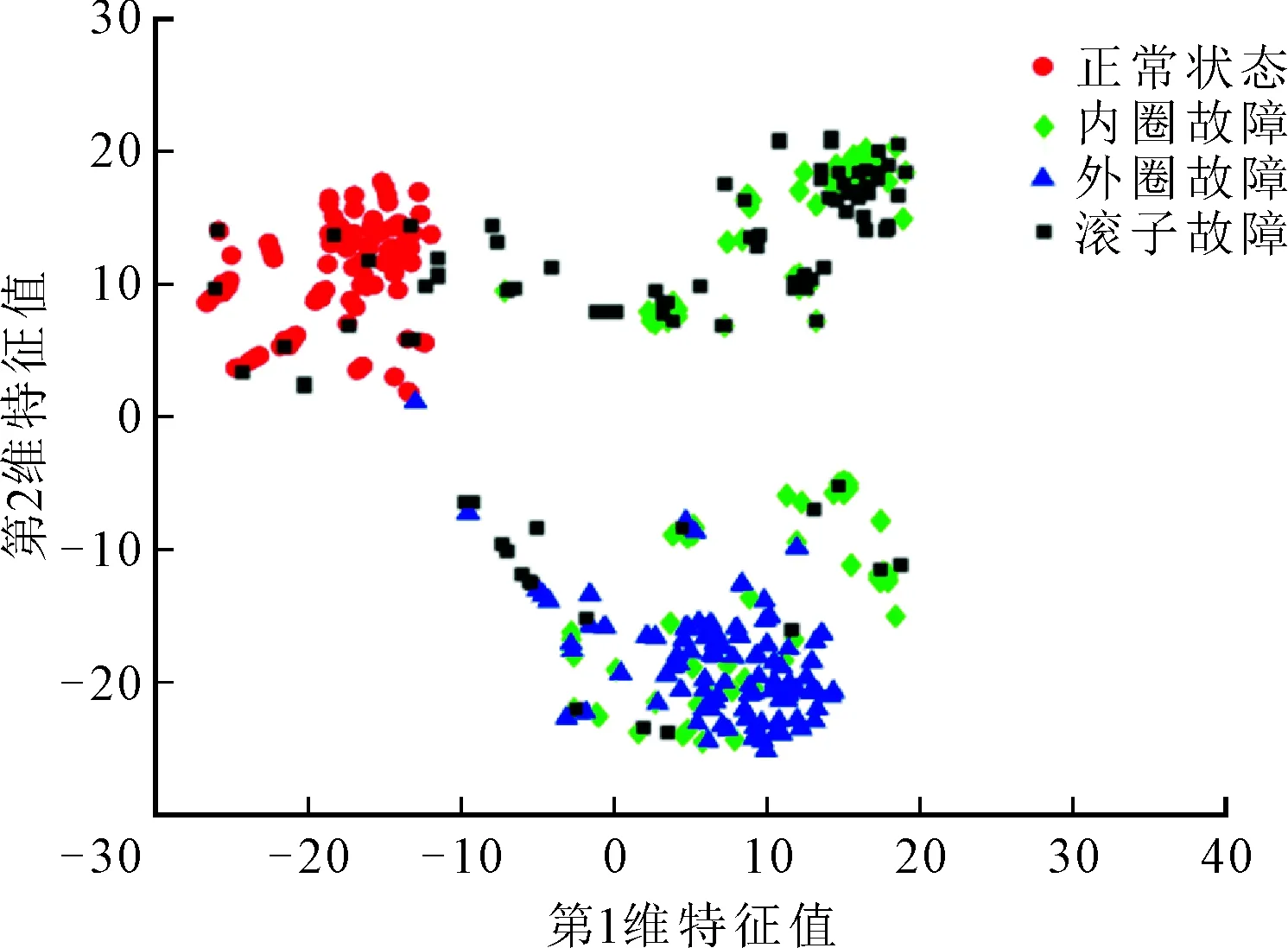
(b)TSNE

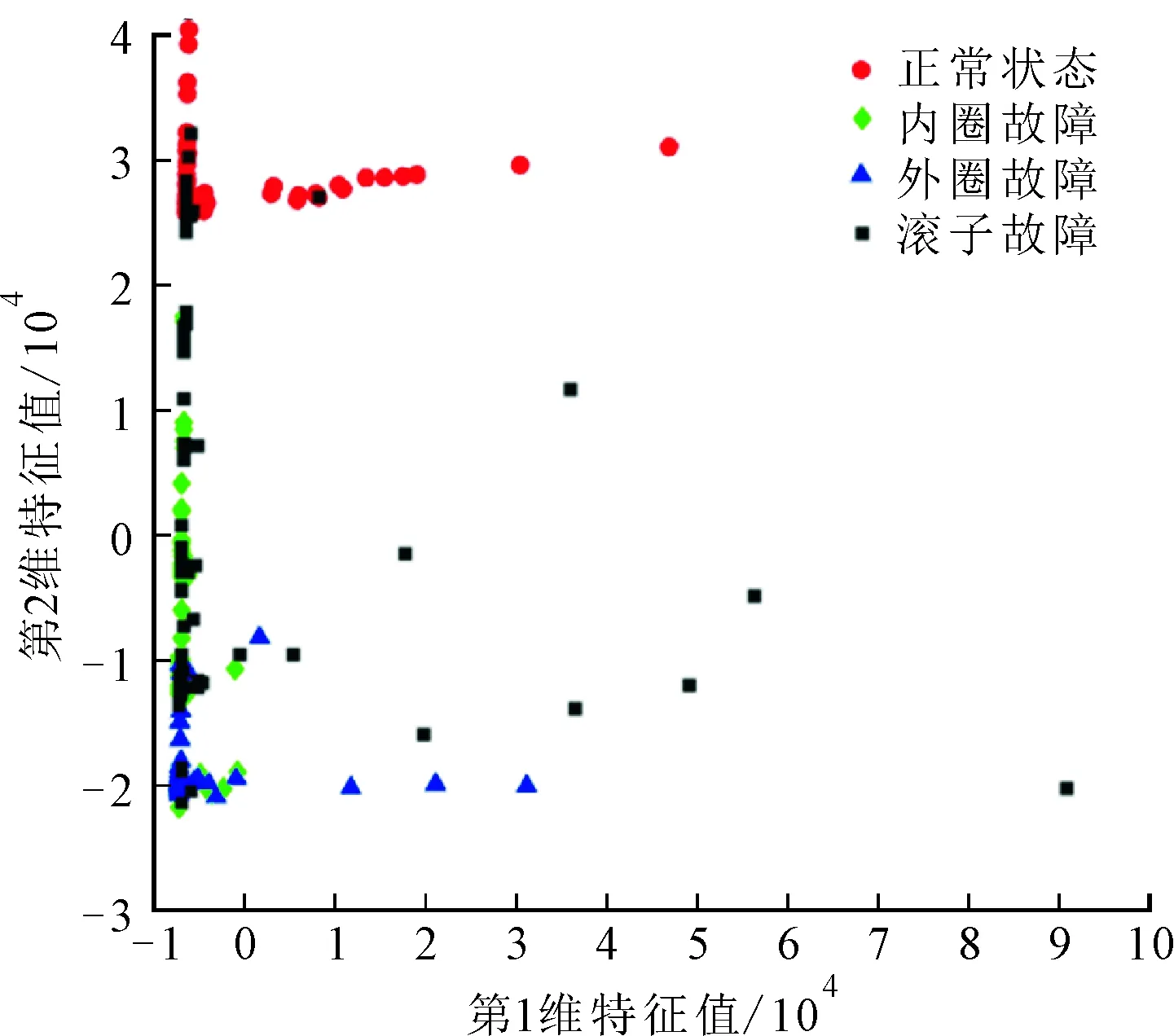
(c)PCA图9 不同方法原始特征降维效果的比较

从表1可以看出,MDS降维提供了最佳的类间距与类内距的比,并且与另外两种方法存在较大差距,优势明显。与直接对原始特征做MDS相比,特征选择后再做MDS降维效果更佳。

3.5 模型训练及结果输出

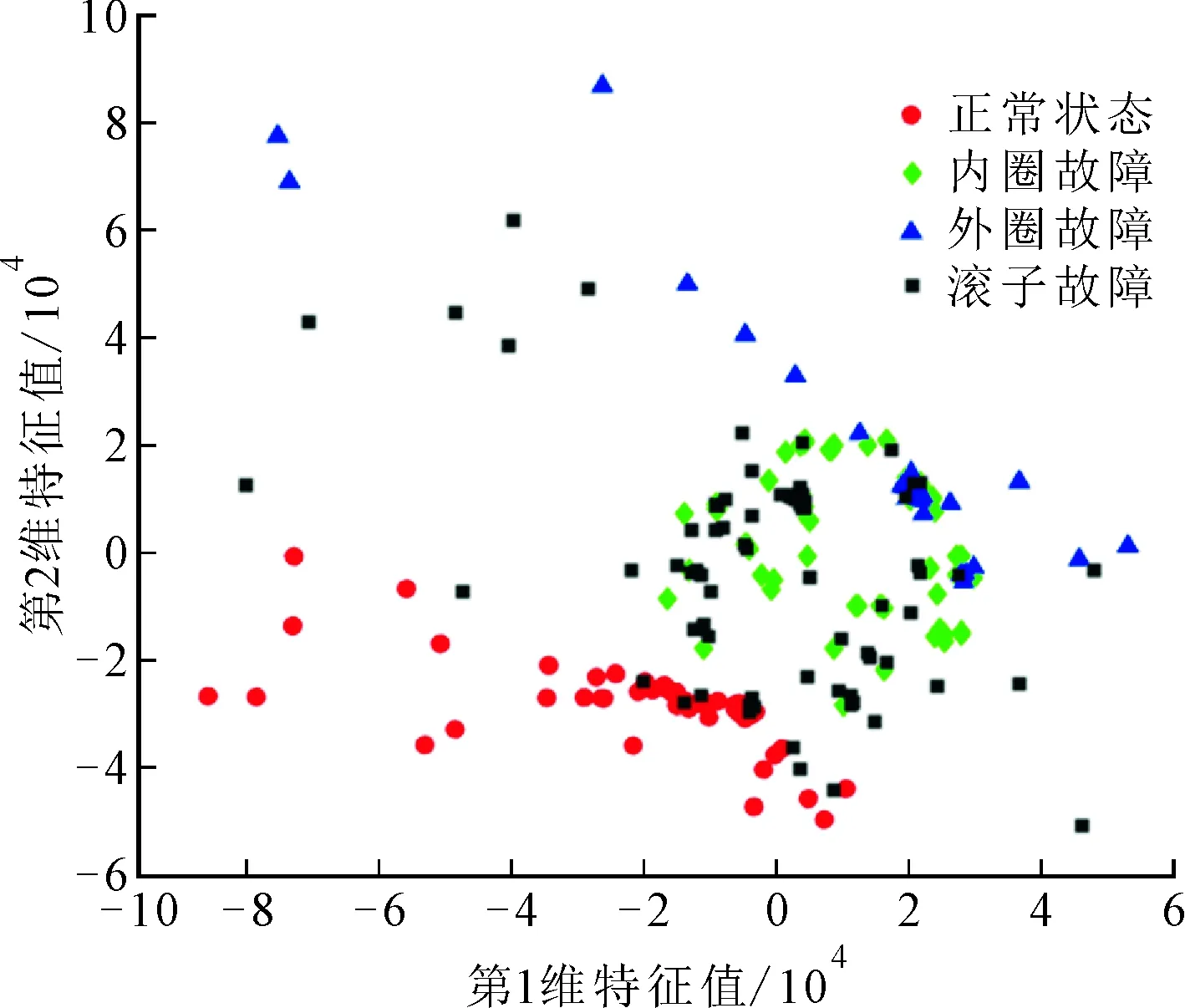
(a)MDS

(b)TSNE

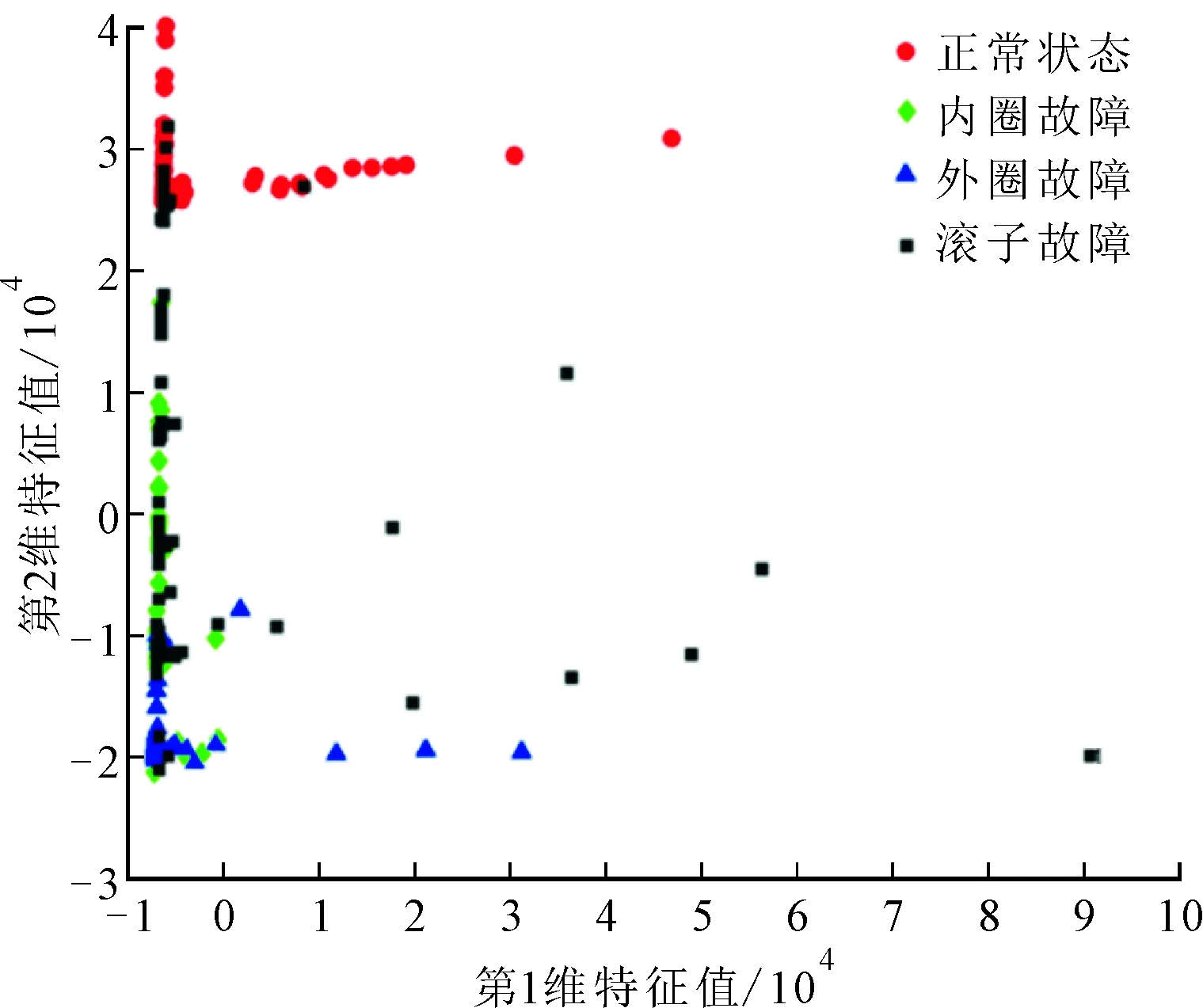
(c)PCA图10 不同方法特征选择后降维效果的比较

从表2的模型输出结果中可以看出,依据特征重要性排序的特征选择和多维缩放的降维方式对提高分类准确率均有贡献。特征选择后测试集中的分类准确率由95%提高至97.5%,再经过MDS降维准确率上升至100%。表1中3种方法下测试集的分类混淆矩阵如图11所示。0、1、2、3分别代表正常、内圈故障、外圈故障、滚子故障,对滚子故障的正确分类有助于提升分类准确率。

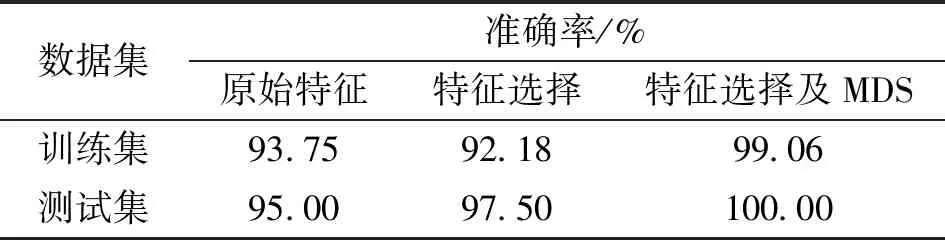
表2 不同特征处理方式下模型准确率对比

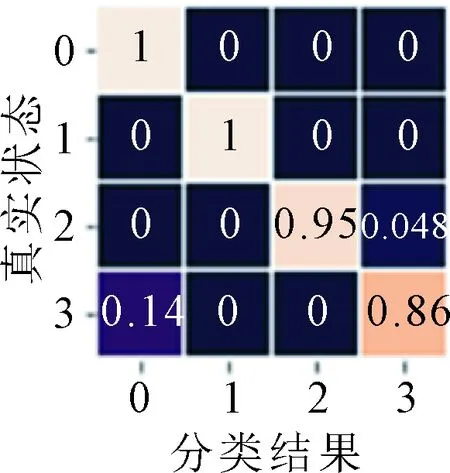
(a)原始特征 (b)特征选择 (c)特征选择+MDS

图11 不同特征处理方式下测试集分类混淆矩阵

4 结 论

本文提出了使用MDS和随机森林的滚动轴承故障诊断方法。首先提取滚动轴承振动信号自相关函数的FDA拟合系数,构造故障特征集;然后使用MDS对依据重要性排序选择过的特征进行压缩,减小模型时间复杂度与运算复杂度,并避免可能存在的干扰;最后将处理后的特征送入随机森林分类模型,对滚动轴承的故障状态进行诊断。为验证所提方法的有效性,与TSNE-RF和PCA-RF作对比,得到如下结论。

(1)将轴承振动信号自相关函数的FDA拟合系数作为样本特征时,在RF分类器中准确率达到了95%,验证了本文所用特征提取方法的可行性。

(2)在与TSNE-RF和PCA-RF的对比实验中,MDS降维后的类间距与类内距的比值明显高于其余两种方法,并在特征提取后有所提升,验证了本文所用特征选择和MDS降维方法的有效性。

(3)使用特征选择和MDS、RF对正常状态及3种故障下的滚动轴承进行故障诊断,测试准确率均达到100%,较未使用MDS的RF分类器提升了5%,验证了本文所提MDS与RF结合方法的有效性。