基于解方程组的替代定理的证明方法

文/吴志刚

1 问题的提出

电路分析中的替代定理，是指：如果已知电路中某条支路的电压U 或电流I，那么无论该条支路是由何种元件构成的，它都可以用一个电压源U 或者电流源I 来代替该支路，替代之后，整个电路的电压和电流均不变。

可以参照图1来解释该定理：图1（a）的电路中，第k 支路的电压U0 和电流I0 已知，则根据替代定理，可以将该支路用电压源U0或者电流源I0 来代替，而不会对原电路产生影响，在图1（b）中用电流源I0 来代替原支路k。

对于该定理的证明，在电路分析方面的教科书中大多采用文字描述性的方法，似乎有点欠缺说服力，本文则给出严格的数学证明，证明过程严谨，不容易产生歧义，具有较强说服力。

2 证明过程

2.1 证明思路

对图1中的a、b 两个电路，欲求各个支路的电压和电流，分别根据基尔霍夫电压定理（KVL）、基尔霍夫电流定理（KCL）和每个支路的伏-安关系列方程组，如果两个电路的方程组解出来的结果相同，也就是说对应支路的电压和电流都相同，则说明用电流源I0 来代替原电路的k 支路，对原电路没有影响。下面就分别对图1的a、b 两个电路分别列方程求解。

2.2 解原电路的方程

原电路即为图1(a)电路，假设它总共有b个支路和n 个节点，根据基尔霍夫电压定理、基尔霍夫电流定理以及各支路的伏-安关系，可以列出以下总共2b 个方程：

除去支路k 外其余部分支路的伏-安关系：b-1 个

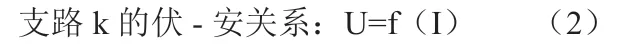
注意，在上面所列的方程中，单独把第k支路的伏-安关系（2）列出来，其它的方程统称为方程组（1）。

接下来解上述方程组，先看方程组（1）：

对于方程组（1）而言，它的未知数是图1（a）中各个支路的电压和电流，根据假设，共有b 个支路，因此有2b 个未知数，但是方程组1 中的方程个数为：

KCL 方程数（n-1 个）+KVL 方程数（b-（n-1）个）+除去支路k 外其余部分支路的伏-安关系方程（b-1 个）=2b-1 个

即方程个数为2b-1 个，未知数为2b 个，方程个数比未知数少1 个，因此，方程组（1）的解无法确定，但是如果利用线性代数中自由变量的概念，把第k 支路的电流I 看作自由变量，则方程组（1）中每一个未知数都可以表示成第k 支路电流I 的函数，特别的，根据方程组（1）可以把第k 支路的电压U 也表示成第K 支路电流I 的函数，即：

联立式（3）和第k支路的伏-安关系式（2），即U=f（I），得到：解上面方程组就可以得到第k 支路的电压和电流。解出的电压和电流是曲线U=g（I）和曲线U=f（I）的交点，分别是记为U0 和I0，其示意图见下面图2。利用解出的I0，带入方程组（1），可以得到图1(a)电路的所有参数。从图2可以看出，在曲线U=g（I）上，I0 点对应的电压是U0，这一点在下面的证明中需要用到。

2.3 解替换后的电路的方程

替换后的电路为图1(b)电路，同样的方法可以列出下面的2b 个方程：

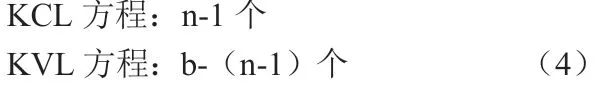
除去支路k 外其余部分支路的伏-安关系：b-1 个

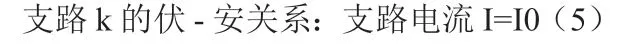
在上面所列的方程中，也单独把第k 支路的伏-安关系（5）单独列出来，其它的方程统称为方程组（4）。

由于采用电流源代替原电路的k 支路后，a、b两个电路的拓扑关系相同，因此，方程组（4）和方程组（1）中所含的基尔霍夫电流方程和基尔霍夫电压方程都一样；又因为电路其余部分元件也没有改变，因此，除了第k 支路外的电路其余部分的伏-安关系也不变，所以方程组（4）和方程组（1）是相同的。

接下来解图1(b)电路的方程，先解方程组（4）：

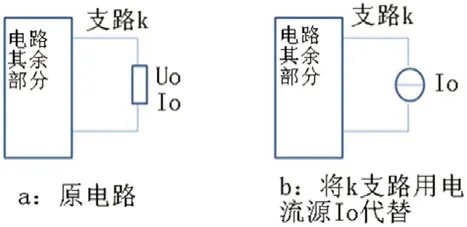
图1：替代定理

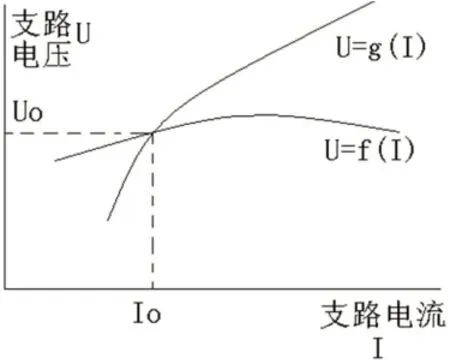
图2：图1中（a）电路解的示意图

由于方程组（4）同样有2b 个未知数和2b-1 个方程，并且方程组（4）和方程组（1）相同，因此从方程组（4）得到的U 和I 的关系也是式（3）：U=g（I），于是联立式（3）和第k 支路的伏-安关系式（5），得到：

解上面方程组，将（5）式中I=I0 代入（3）式：U=g（I）=g（I0）从图2中又可以看到，在曲线U=g（I）上，I0 点对应的电压是U0，即g（I0）=U0，因此，如果用电流源I0 代替k 支路，所得到的电路在k 支路上的电压也是U0，和原电路（a）在k 支路上的电压是相等的。将I0 代入方程组（4），可以解出图1（b）电路中其它所有参数，并且都等于图1（a）电路中的相应参数，因此可以用电流源I0 替代k支路，于是替代定理得到证明。用电压源替代的情况可以用类似的方法证明。

3 总结

采用本文的证明方法，整个过程是严格的数学证明，不容易产生歧义，而且相对简单明了，不失为一种好的参考方法。