基于MMSE-MLSA与感知滤波的语音增强算法
董 胡,马振中,赵 娜,刘 刚,童 欣
(长沙师范学院 信息科学与工程学院,湖南 长沙 410100)
0 引 言
当前,常见的语音增强算法众多,诸如:谱减法、维纳滤波法、小波包去噪、MMSE-LSA法等。谱减法及维纳滤波法总体来说计算量稍小,易实现,但也易出现音乐噪声[1-5]。小波包去噪法有较强的时频分析能力,适合非平稳信号处理,但阈值的设定是小波包去噪的关键点,阈值太大或太小都将影响去噪效果[6-8]。MMSE-LSA算法的语音增强效果优于谱减法、维纳滤波法和小波包去噪法,但需要预测或假设语音频谱的分布,在低信噪比的复杂噪声环境下,其语音增强效果有待改善[9-10]。
针对上述语音增强算法所描述的问题,提出了一种改进对数谱幅度最小均方误差谱估计(MMSE-MLSA)与感知滤波结合的语音增强算法。该算法将降噪和噪声掩蔽进行单独处理,首先采用MMSE-LSA对含噪语音进行初级降噪,接着使用感知滤波器将初级降噪后残余噪声掩蔽掉。仿真实验结果表明,在低信噪比的复杂噪声环境下,与常见的谱减法及MMSE-MLSA相比较,该算法增强后的语音失真及残余音乐噪声更小,增强效果更明显。
1 语音增强算法原理
图1显示了文中算法的原理。含噪语音信号先通过改进对数谱幅度最小均方误差谱估计作增强处理,然后使用感知滤波器掩蔽上一级增强信号中的残余噪声,最终获得增强后的语音。从图1可知,整个增强算法分为四个部分:MMSE-MLSA谱估计、噪声估计、掩蔽阈值估计和感知滤波器。
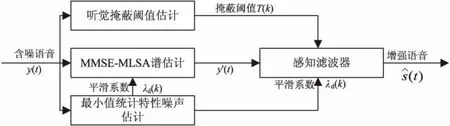
图1 MMSE-MLSA语音增强算法原理
1.1 MMSE-MLSA谱估计
设s(t)为纯净语音信号,n(t)为噪声信号,y(t)为含噪语音信号,若仅考虑加性噪声,有如下表达式[11-12]:
y(t)=s(t)+n(t)
(1)
令Y(k)、S(k)、N(k)分别表示y(t)、s(t)、n(t)作FFT变换后所对应的第k个频谱幅度,并假设语音与噪声统计是独立的,则有:
Y(k)=S(k)+N(k)
(2)
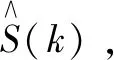
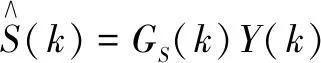
(3)
相比于MMSE估计法[13],MLSA-MMSE估计法更适合人耳的听觉特性,能更好地抑制噪声,故文中语音增强算法初级选择MLSA-MMSE估计法。对MLSA-MMSE估计法的谱增益函数GS(k)作如下定义:
(4)
其中,ξ(k)为先验信噪比;γ(k)为后验信噪比,则有[14]:
(5)
γ(k)=Y2(k)/λn(k)
(6)
v(k)=ξ(k)γ(k)/(1+ξ(k))
(7)
假设H0(k)和H1(k)分别表示语音缺失和存在,并且假设对于语音和噪声短时傅里叶变换系数的复高斯分布,信号的条件概率密度作如下定义:
(8)
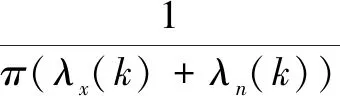
(9)
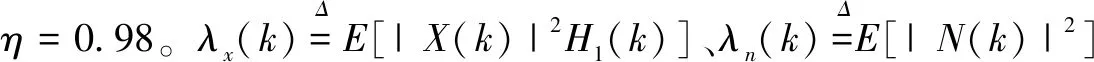
(10)
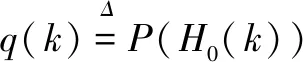
令A=|S|代表语音谱幅度,谱增益函数Gmin作如下定义:
exp{[logA(k)|Y(k),H0(k)]}=Gmin.|Y(k)|
(11)
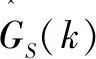
(12)
1.2 噪声估计
作为语音增强算法中的重要组成部分,如果噪声估计过高,则弱语音将被消除,增强后的语音将出现失真;如果估计过低,则增强后的语音将残留过多的噪声。基于最小值统计特性,估计算法能使估计的噪声较好地跟踪噪声改变。所以,在该算法中,噪声估计选择最小值统计特性算法。
1.3 听觉掩蔽阈值估计
听觉掩蔽是听觉系统的一个心理声学特性,在音频编码中应用广泛。通过模拟人耳的频率选择特性和掩蔽特性来计算掩蔽阈值。在对掩蔽阈值作计算之前,语音谱需作粗略估计。其中,语音谱的粗略值可通过下式进行估计:
(13)
1.4 感知滤波器
含噪信号经初级增强后,存在一定的残留噪声,其可以被人耳的听觉掩蔽特性掩盖而不被完全去除。如果它被完全去掉,则可能降低语音的可懂度,导致语音失真。因此,基于听觉掩蔽效应的感知过滤器被用作过滤处理。
|G(k)|2×|N(k)|2≤T(k)
(14)
其中,T(k)为掩蔽阈值。
感知滤波器模型定义如下:
(15)
其中,0<θ<1。通过实验取θ=0.8。
2 实验与结果分析
实验用的语音数据采样率为16 kHz,帧长为512,重叠1/2,每一帧添加Hanming窗。实验用的噪声来自Noisex-92数据库中的白噪声、factory噪声和M109坦克噪声。将上述噪声信号和纯净语音信号混合成10 dB、5 dB、0 dB、-5 dB的含噪语音信号。
分别采用谱减算法、MMSE-LSA算法及文中提出的算法对含噪(M109)语音作增强处理,结果如图2所示。从图2可知,对于语音信号中语音幅值较弱的部分,谱减算法和MMSE-LSA算法的增强效果都不佳,尤其是谱减算法,几乎完全丢失了语音幅值较弱的信号;而文中提出的算法不仅能较好地去除含噪语音中的M109噪声,同时能较好地恢复出原来语音幅值较弱的部分。
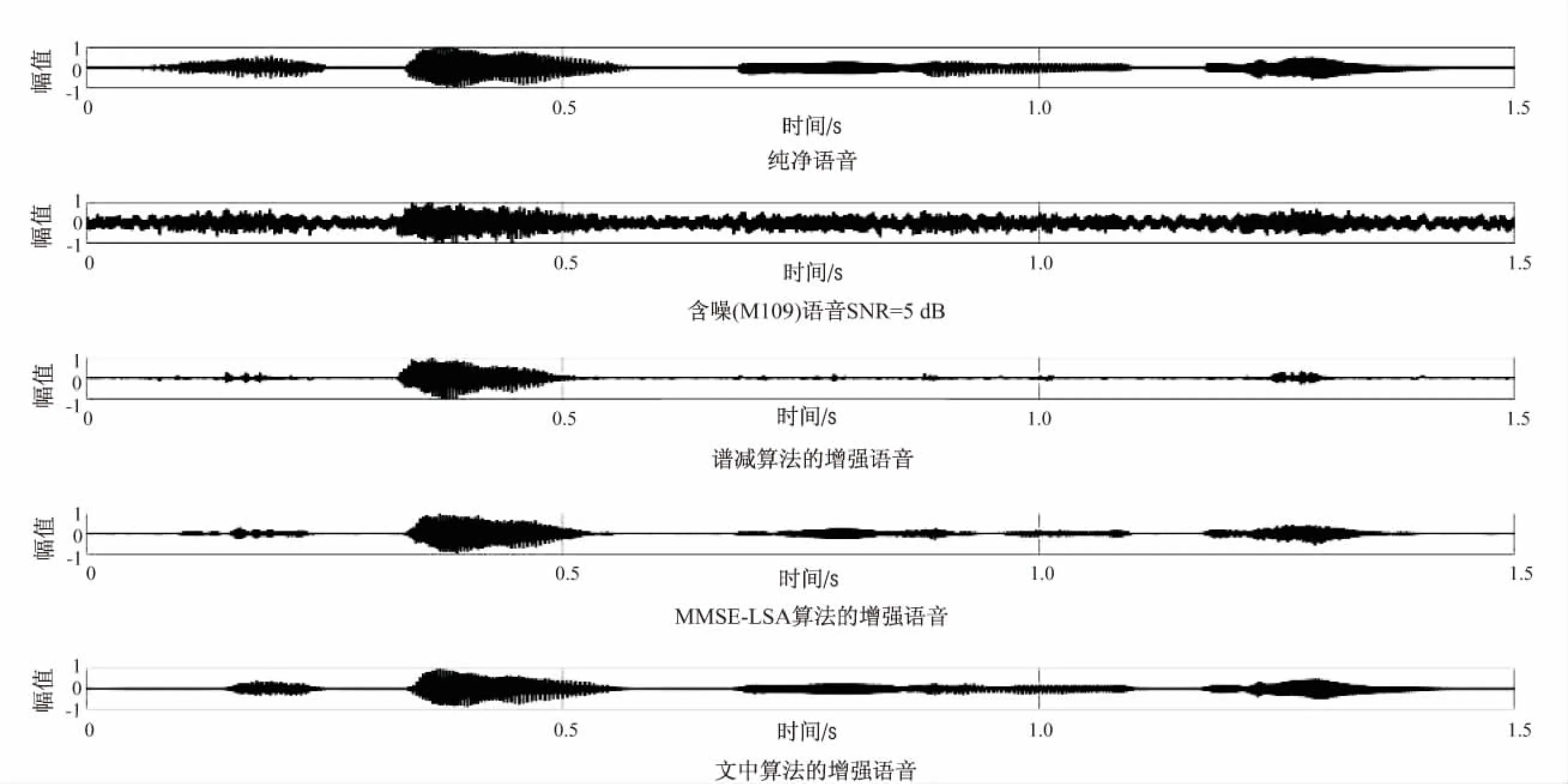
图2 含噪(M109)语音SNR=-5 dB的语音增强结果
2.1 分段信噪比(SEGSNR)
利用SEGSNR的提高量来衡量噪声的衰减量:
(16)
其中,L表示帧数;N表示帧采样点。
通常SEGSNR越大,表示信号中包含的噪声和语音失真越小,相应波形越接近纯净语音。
对一定信噪比的含噪语音分别采用谱减法、MMSE-LSA和文中算法进行语音增强仿真测试,结果如图3所示。可以看出,文中提出的语音增强算法SEGSNR提高量最大。
2.2 MOS得分
MOS得分测试由10名本专业学生(男女各5人)进行语音试听,由试听者对原始语音和增强后语音作对照测听,给出主观得分,结果如图4所示。

图4 各种算法在不同SNR下的MOS得分
从图4可知,文中算法的MOS得分最高,MMSE-LSA次之,谱减法增强后语音中存在更多的残余音乐噪声,且主观听觉较差,因此增强后的得分最低。而文中算法对增强后的信号中的噪声作掩蔽处理,因此主观评价较高,虽然存在少量的背景噪声,但音乐噪音的减少更明显,主观听觉更好,分数更高。
3 结束语
文中提出了基于MMSE-MLSA与感知滤波的语音增强算法。语音增强算法分为两级,初级采用MMSE-MLSA对含噪语音作谱估计增强处理,去除含噪语音中的大部分噪声。针对初级语音增强中存在的残余噪声,次级使用感知滤波器对初级增强后的信号进行感知滤波,进一步去除信号中的残余音乐噪声。仿真实验结果表明,在低信噪比的复杂噪声环境下,与谱减算法及MMSE-LSA算法相比较,该算法能有效降低语音失真及去除残余音乐噪声,语音增强效果更明显。

