基于GA-RBF融合算法的玉米病虫害产量损失预测研究

王冬雪　陈桂芬　李英伦　史树森

摘要：鉴于玉米病虫害等影响因素在预测玉米产量损失时所具有的复杂及非线性等特点，采用传统的径向基函数（radial basis function，简称RBF）神经网络预测起来相对较难，且其预测精度较低。针对上述问题，提出1种基于遗传算法（genetic algorithm，简称GA）和径向基函数神经网络相融合的优化算法，对病虫害所造成的玉米产量损失进行预测。该融合算法利用人工神经网络的非线性拟合能力强和遗传算法寻优能力强的优点，建立最优产量损失预测模型，将该模型的估算值与玉米产量的实际值进行拟合，得到较好的拟合效果图。为了验证算法的可行性，以国家863计划示范基地榆树市弓棚镇13号村的试验数据为样本数据进行仿真预测。结果表明，经过GA-RBF融合算法的预测误差为0.207，较优化前误差降低了0.151，预测精度得到提高，实现对玉米病虫害产量损失的有效预测。预测结果可为农民进行科学有效的病虫害防控提供科学依据，经济有效地降低受灾程度，提高玉米产量。

关键词：遗传算法;RBF神经网络;融合算法;玉米病虫害;产量损失预测模型

中图分类号： TP312;S126文献标志码： A

文章编号：1002-1302（2019）09-0263-04

玉米不仅作为东北地区的主要粮食种植作物，而且在整个粮食生产中也具有重要的地位。病虫害是影响玉米产量的重要因素之一，现阶段病虫害频发对玉米的产量及质量造成了极大的威胁[1-3]。病虫害农业产量损失预测与防治已成为农业经济发展中一个不可或缺的环节。因此，对其进行研究和分析预测具有较强的实际指导意义。

鉴于玉米病虫害等影响因素在预测玉米产量损失时所具有的复杂及非线性等特点[4]，采用传统单一的人工神经网络对其进行预测不仅相对困难，且预测精度不达标，在解决样本量少、噪声多的问题时整体效果达不到预期。神经网络技术虽在各个领域均有不同的应用，但仍然存在一些难以解决的问题[5]，因此须对其进行相应的改进，使其发挥良好的预测作用。

针对以上问题，本研究提出一种基于遗传算法（genetic algorithm，简称GA）与径向基函数（radial basis function，简称RBF）神经网络融合的优化算法，这种基于遗传算法和神经网络的GA-RBF融合算法不仅可以充分发挥神经网络良好的映射能力，而且可以提高RBF神经网络的收敛及自适应学习能力，在处理产量损失预测时具有独特的优势。通过融合后的优化算法建立GA-RBF预测模型，对玉米病虫害的产量损失进行预测。根据预测结果分析病虫害的发生动态对玉米产量的影响程度，可使种植者及时防治灾害，经济有效地降低受灾程度，提高玉米产量。

1 研究方法

1.1 GA-RBF优化算法模型的构建

本研究主要采用MATLAB软件，采用的技术路线分为3个部分：首先，利用遗传算法工具箱优化RBF神经网络;然后，将优化后的RBF神经网络与遗传算法融合，建立新的 GA-RBF 工具箱;最后，构建产量损失预测模型。

1.1.1 优化指标的选取

通常在通过遗传算法优化设计神经网络时[6-8]，最关键的步骤是对神经网络各参数的选择，即数据中心ci、扩展常数（宽度）σi以及权值wi大小的选择。本研究主要是通过遗传算法对神经网络的宽度及中心值进行精确的选择以及优化，只有选择了精确的参数值，才能更好地发挥RBF神经网络的逼近效果，提高预测精度。

首先需要对径向基神经网络隐含层的基函数g（x）进行选择，不失一般性，选择的隐含层基函数为径向基神经网络中常被选用的高斯函数[9]。并最终确定其在径向基神经网络中的激活函数为：

式中：x=（x1，x2，…，xn），为网络输入矢量;ci=（ci1，ci2，…，cin）为隐含层中心矢量（所属第i个神经元），与x具有同样的维数;σi是第i个基函数的宽度;m是隐含层神经元的数量;‖x-ci‖ 表示矢量x、ci之间的欧式范数[10]。其完成的非线性映射方程如下：

式中：X∈Rn是输入矢量;φ是1个R+→R的非线性函数[11]。

在确定RBF神经网络对应的函数以及相应参数后，将通过遗传算法对其进一步优化及修正。

1.1.2 优化流程

1.1.2.1 训练样本的预处理

采取归一化方法[12]对数据样本进行处理：

式中：xpi为第p个样本的第i个变量的原始数据;x′pi为第p个样本的第i个变量的归一化处理数据。预处理后的样本数据范围为（0，1）。

1.1.2.2 对应于RBF的遗传编码

在本研究提出的算法中，主要思想是让RBF神经网络的宽度同中心一起，通过遗传算法对其进行优化和修改。常用的编码包括二进制法和实数编码法[13]。由于本研究中是对网络结构的中心及宽度进行优化，选择的中心值较大，若采取二进制编码法，会造成计算量大的缺点。因此，最终决定采用实数编码法进行编码，这种方法比较直观简单，减少了编码过程及计算量，方便神经网络隐含层的设计，提高了网络的训练速度、运行效率及识别精度。

1.1.2.3 创建初始种群

试验时，设定遗传算法的初始种群数为20个，最大进化代数为1 000。初始种群，即初始基函数g（x）的中心值。

1.1.2.4 構造适应度函数

在进行网络训练时，原始数据样本分为训练数据集和测试数据集。通过训练误差和网络规模来确定相应网络的适应度。适应度函数在选取时需要依据具体问题的情况来确定，且该函数须保证为非负[14]。通过遗传算法对RBF网络进行编码后，网络以输入、输出数据作为样本训练数据集，运行后以所有训练数据集的输出与期望值的误差平方和的倒数作为适应度函数，得到的适应度函数能够较好地反映个体性能的差异。适应性函数的取值是衡量算法的一个关键信息，也是能否找到最优解的关键[13]。

采用的适应度函数如下：

式中：L、p为样本数;d为实际输出;y为预测输出。

1.2 仿真参数的设置

遗传算子的赋值[15-16]：通过选择、交叉、变异等遗传操作，可以产生新一代种群，并逐渐演变为近似最优解的最优状态。遗传算法是一个迭代过程，每次迭代都会保留一些候选的解决方案以及排序的利弊，这些解决方案是根据遗传算子的指标选择和计算，产生的新一代候选解决方案，最终使目标达到收敛。

（1）选择率（代沟）：经多次计算试验认为，比值为0.8时，进行选择方法的转换是比较合适的。通过比例选择法确定比值[17]，计算公式如下所示：

pi=Fi∑F;i=1，2，3，…，m。（6）

（2）交叉率：通常来说，交叉概率的取值在0.5～1.0之间，不宜过小。因为交叉概率太小会使搜索停滞[18]。本研究中交叉概率的取值经计算选择0.7。所采用的“实数交叉法”操作如下：

akj=akj（1-b）-akjbalj=alj（1-b）+aljb。（7）

式中：akj、alj分别为第k、l个染色体在j位进行的交叉操作;b为[0，1]间的随机数。

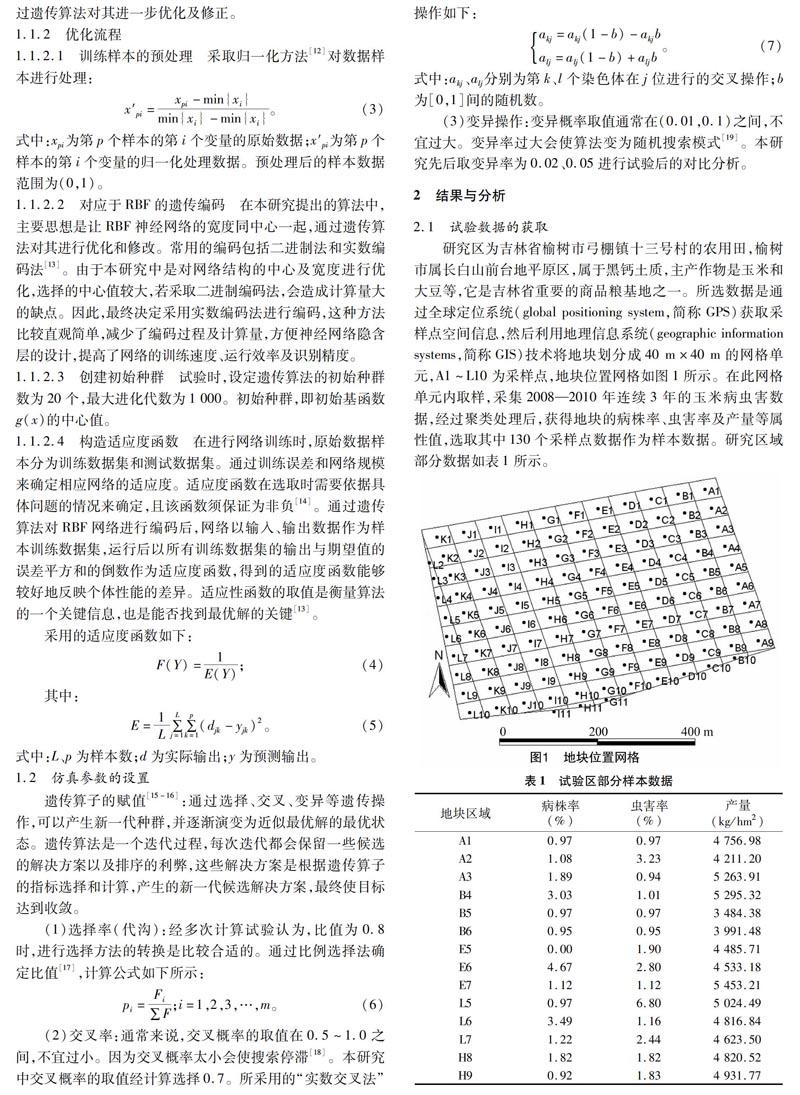
（3）变异操作：变异概率取值通常在（0.01，0.1）之间，不宜过大。变异率过大会使算法变为随机搜索模式[19]。本研究先后取变异率为0.02、0.05进行试验后的对比分析。

2 结果与分析

2.1 试验数据的获取

研究区为吉林省榆树市弓棚镇十三号村的农用田，榆树市属长白山前台地平原区，属于黑钙土质，主产作物是玉米和大豆等，它是吉林省重要的商品粮基地之一。所选数据是通过全球定位系统（global positioning system，简称GPS）获取采样点空间信息，然后利用地理信息系统（geographic information systems，简称GIS）技术将地块划分成40 m×40 m的网格单元，A1～L10为采样点，地块位置网格如图1所示。在此网格单元内取样，采集2008—2010年连续3年的玉米病虫害数据，经过聚类处理后，获得地块的病株率、虫害率及产量等属性值，选取其中130个采样点数据作为样本数据。研究区域部分数据如表1所示。

2.2 部分MATLAB代码

通过遗传算法对RBF神经网络进行优化的部分MATLAB代码如下：

net=newrb（train_x，train_y，0.01，1，5，1）;

%构建神经网络

Test_y=sim（net，test_x）;

FieldDD=rep（RANGE，[1，NVAR]）;

Chrom=crtrp（NIND，FieldDD）;

%创建初始种群

gen=0;

ObjV=objfuns（net，Chrom，train_x，train_y）;

%计算初始目标函数值

tic

while gen

FitnV=ranking（ObjV）;

%分配适应度值（Assign fitness values）

SelCh=select（‘sus，Chrom，FitnV，GGAP）; %选择

SelCh=recombin（‘xovsp，SelCh，0.7）;%重组SelCh=mutbga（SelCh，FieldDD，[0.05，1]）;%变异

ObjVSel=objfuns（net，SelCh，train_x，train_y）;

%计算子代目标函数值

[Chrom ObjV]=reins（Chrom，SelCh，1，1，ObjV，ObjVSel）;

gen=gen+1;

trace（gen，1）=min（ObjV）;

trace（gen，2）=sum（ObjV）/length（ObjV）;

2.3 仿真结果分析

2.3.1 确定变异算子

变异算子的确定是本研究中衡量预测是否合理化的一个关键。在遗传算法中，变异操作是不可或缺的，变异率的选择是产生新基因必不可少的辅助方法[20-22]。因此，选择适当的变异率是整个寻优过程中的一个重要步骤，若变异率过大，会造成算法变为随机搜索方法。

根据试验样本数据集，最终设定RBF神经网络的输入层神经元为2个，即玉米病株率与玉米虫害率;输出层神经元为1个，即玉米产量;利用迭代方法来设计训练RBF神经网络，通过训练，逐渐增加迭代次数，每迭代1次网络结构就增加1个神经元，直到误差平方和低于目标误差，或网络神经元的数目达到最大值时，迭代停止。本试验最终得到1个含有5个隐层神经元的网络模型。

为选出适当的变异率进行操作，先后分别采用变异率为0.02、0.05进行仿真试验。试验结果如图2、图3所示。

通过仿真试验，对部分数据进行归一化处理后，得到2种不同变异率情况下的预测结果，对预测结果进一步计算后得出：變异率为0.05时的预测精度高于变异率为0.02时的预测精度。因此，在对比后采用了0.05的变异率进行最终预测。通过对比2种预测结果，可以看到变异率为0.05时，产量预测整体归一化趋势较好，且采用GA-RBF融合算法进行玉米病虫害产量预测的相对误差要小，预测精度较传统单一的RBF神经网络得到了提高。

由此可见，对遗传算法变异率的选择是一个十分重要的

过程[23-25]，选择合适的变异率才会使算法达到最优。

2.3.2 预测误差的比较

为将误差进行对比，在经过多次仿真试验后，得到如下结论：随着网络训练集样本的数量逐渐增加，本研究所提出的GA-RBF融合算法相较于传统的RBF网络而言，无论是在收敛速度或是在网络逼近的准确性上均有所提高且网络的全局搜索能力较好。本研究依次采用3种不同算法来分别测试样本数据。

由表2可以看出，对于预测精度来说，本研究构建的 GA-RBF 模型，预测误差为0.207，明显优于RBF网络和BP网络;在处理速度方面，在預测10个样本的情况下，GA-RBF网络较单一的RBF网络和BP神经网络速度均有提高。

同时，为了验证算法的准确性，并将预测值与实际值的误差更明显地反映出来，通过优化后的算法工具箱来输出误差曲线，截取部分数据作误差曲线分析，误差结果对比如图4所示。

分析误差曲线可以得出，预测值和实测值偏差较小，表现出较高的预测精度。进一步证明改进算法后的RBF网络比单一的RBF网络和传统的BP网络具有更高的精度和更快的速度，实用性得到了加强。

3 结论

玉米病害、虫害等影响因素是影响玉米产量损失的重要因素之一，其所具有的复杂特性导致在使用传统单一的神经网络进行预测时相对困难，且预测精度不够理想。因此，针对以上问题，本研究提出1种基于遗传算法和径向基函数神经网络相融合的优化算法，对玉米病虫害所造成的玉米产量损失进行预测。研究结果表明，基于遗传算法优化后的RBF神经网络模型，可实现对玉米病虫害产量损失的有效预测。该模型能够较好地处理病虫害影响因素与玉米产量损失之间的非线性关系，效果优于传统的预测模型，作为一种定量模型可有效用于病虫害的适时防控工作。通过计算分析后得出，采用单一RBF神经网络模型对样本数据集进行训练时，所得到的预测误差为0.358 01;而经过GA-RBF融合算法的预测误差为0.207，较优化前的误差降低了0.151。由此可见，经 GA-RBF 融合算法优化参数后，玉米产量损失预测精确度得到了提高。经过多次仿真试验验证，当网络的训练样本数增加时，本研究提出的GA-RBF融合优化算法较传统RBF网络在收敛速度和网络逼近的准确性上相对提高，其网络的全局搜索能力较好。从整体上而言，预测结果与实际影响产量损失相对吻合，取得了良好的预测效果，对玉米农作物在防虫工作中起到了有效的参考作用。

本研究主要从影响玉米产量的空间区域来研究玉米产量损失的预测，没有考虑时间特性和其他因素。今后，随着实践的不断深入，数据的积累不断丰富，将继续进行深层次多方面的研究。

参考文献：

[1]姜玉英，曾 娟，陆明红. 2015年全国农作物重大病虫害发生趋势预报[J]. 中国植保导刊，2015（2）：10-12.

[2]刘 杰，姜玉英. 2012年玉米病虫害发生概况特点和原因分析[J]. 中国农学通报，2014，30（7）：270-279.

[3]孙甜田，范作伟，刘淑霞，等. 吉林省不同熟期玉米病虫害发生情况[J]. 中国农学通报，2014，30（30）：222-227.

[4]符保龙. RBF网络在农业病虫害预测中的应用研究[J]. 安徽农业科学，2008，36（1）：388-389.

[5]刘 璇，唐慧强，许遐祯，等. 基于神经网络的农业病虫害损失预测[J]. 农机化研究，2009，31（4）：13-16.

[6]刘鲭洁，陈桂明，刘小方. 基于遗传算法SVM参数组合优化[J]. 计算机应用与软件，2012，29（4）：94-100.

[7]Chen G F，Dong W，Jiang J，et al. Variable-rate fertilization decision-making system based on visualization toolkit and spatial fuzzy clustering[J]. Sensor Letters，2012，10（1）：230-235.

[8]曹丽英. 玉米主产区土壤养分与玉米产量的时空变异及其相关性研究[D]. 合肥：安徽农业大学，2013.

[9]旷 岭. RBF神经网络的粮食产量预测[J]. 计算机仿真，2011，28（11）：189-191，200.

[10]张方舟，郝庆辉，周 勃，等. 遗传算法的RBF神经网络在线损计算中的应用[J]. 计算机技术与发展，2014，24（6）：192-195，199.

[1]庄 健，杨清宇，杜海峰，等. 一种高效的复杂系统遗传算法[J]. 软件学报，2010，21（11）：2790-2801.

[12]王铭泽，关新红，闫吉府，等. 股票的GA-RBF预测模型[J]. 辽宁工程技术大学学报（自然科学版），2014，33（7）：970-973.

[13]张 纪. 基于遗传算法优化神经网络的粮食产量组合预测研究[D]. 新乡：河南师范大学，2015.

[14]Ahmadi M A，Zendehboudi S，Lohi A，et al. Reservoir permeability prediction by neural networks combined with hybrid genetic algorithm and particle swarm optimization[J]. Geophysical Prospecting，2013，61（3）：582-598.

[15]曾 钰. 基于遗传算法优化的RBF神经网络在光伏发电MPPT中的应用[D]. 株洲：湖南工业大学，2015.

[16]Jaddi N S，Abdullah S，Hamdan A R. A solution representation of genetic algorithm for neural network weights and structure[J]. Information Processing Letters，2016，116（1）：22-25.

[17]周维华. RBF神经网络隐层结构与参数优化研究[D]. 上海：华东理工大学，2014.

[18]纪思琪，吴 芳. 基于神经网络的蔬菜病害静态预警模型[J]. 电脑知识与技术，2016，12（10）：189-196.

[19]Hu J，Li D L，Duan Q L，et al. A fuzzy C-Means clustering based algorithm to automatically segment fish disease visual symptoms[J]. Sensor Letters，2012，10（1/2）：190-197.

[20]任艳娜，席 磊，汪 强，等. 粮食产量预测模型的应用与仿真研究[J]. 计算机仿真，2011，28（4）：208-211.

[21]唐 忠，谢 涛. Matlab神经网络工具NNTool的应用与仿真[J]. 计算机与现代化，2012（12）：44-47，54.

[22]龚 纯，王正林. 精通MATLAB最优化计算[M]. 北京：电子工业出版社，2009：2-4.

[23]齐灵子. 大豆食叶害虫危害损失预测模型的研究[D]. 长春：吉林农业大学，2013.

[24]王晓娟. 基于模糊控制与RBF神经网络的桃病虫害发生预测研究[D]. 保定：河北农业大学，2011.

[25]王志敏，方保停. 论作物生产系统产量分析的理论模式及其发展[J]. 中国农业大学学报，2009，14（1）：1-7.