电气化铁路长大隧道区段牵引回流特性研究
朱远帆,陈民武,赵周鉴,孙亮,叶琪
(1. 西南交通大学 电气工程学院,四川 成都 610031;2. 通号(北京)轨道工业集团有限公司 轨道交通技术研究院,北京 102613)
0 引言
近年来电气化铁路在我国中西部地区迅速发展,而中西部地区地形地质条件复杂且多山岭,使得铁路线路出现了较多长大隧道区段。隧道区段接触网采用刚性悬挂方式,没有架设承力索,使隧道区段牵引网阻抗特性与非隧道区段相比存在显著差异[1-2]。此外新建铁路隧道区段均采用无砟轨道,为减小机车对钢轨产生的冲击采用了加厚垫板,增大了两轨之间及轨地之间绝缘,因而增大了钢轨对地泄漏电阻[3]。由于隧道设置防水密封系统,导致经过隧道区段大地的回流较少,钢轨、回流线、综合贯通地线为主要回流路径。同时,长大隧道区段往往伴随长大坡道路段,机车取流进一步增大,使钢轨对地电位进一步抬升。过高的钢轨电位易危及沿线铁路工作人员的人身安全,并导致与钢轨相连的信号设备产生运行故障及加速轨道绝缘垫片老化等问题[4-6]。因此,对铁路隧道区段牵引回流与钢轨电位分布规律进行深入研究具有重大意义。
目前国内外学者对电气化铁路牵引回流及钢轨电位已开展了卓有成效的研究。文献[7]基于Matlab/Simulink仿真平台建立直供带回流线供电方式下高速铁路牵引供电系统仿真模型,对正常运行与短路故障工况下钢轨电流与电位分布情况进行研究。文献[8]从理论角度分析钢轨电位产生机理,并仿真分析上下行钢轨横连、CPW线、支柱基础接地、埋地地线等影响因素对降低钢轨电位的作用及可行性。文献[9]、文献[10]针对重载铁路采用综合接地系统达到降低钢轨电位的作用,研究综合地线半径、埋设深度以及与钢轨横向连线间隔等因素对钢轨电位的影响规律。文献[11]从理论上推导钢轨电流和电位的计算公式,并结合实际工程案例计算分析了回流线、综合地线设置前后钢轨电位变化情况及各回流通路电流分配比例。但上述文献中均未考虑隧道区段的特殊电磁环境及牵引网阻抗参数,不能完全准确地描述隧道区段的牵引回流和钢轨电位的分布规律。
在此,首先建立电气化铁路长大隧道区段直供带回流线供电方式下牵引网链式模型,并计算隧道中各导线阻抗参数,对多导线阻抗及导纳矩阵进行推导,进而建立隧道区段牵引供电系统仿真模型,并在此基础上研究隧道区段牵引回流及钢轨电位分布规律。
1 隧道区段牵引网数学模型
牵引供电网络可视作由平行多导体传输线构成的一个复合链式网络。通过对牵引供电系统中牵引变电所、电力机车和牵引网的特定切割,得到由纵向串联阻抗元件与横向并联导纳元件2部分组成[12]的链式网络(见图1)。设牵引网的平行导体数为m,牵引供电系统由N个切面组成[13],其总体链式电路模型见图2。其中,Zi(i=2,…,N)表示2切面间的阻抗矩阵;Yi(i=1,…,n)表示切面i的导纳矩阵;Ii(i=1,…,N)表示切面i注入的电流源向量。阻抗矩阵及导纳矩阵为m阶方阵,电流源向量I为m维向量。

图1 牵引网等效电路
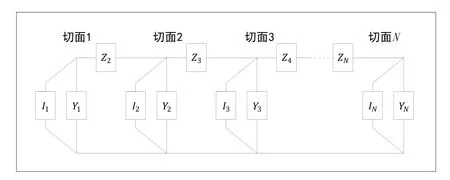
图2 牵引网总体链式电路模型
2 隧道区段牵引网导线参数提取
隧道作为电气化铁路特殊路段,牵引网系统是以接触线和汇流排作为传输导体,钢轨、回流线、综合地线与架空线等作为回流导体构成的复杂多导体传输系统[14]。正确描述隧道区段牵引网数学模型及电气参数是掌握牵引供电系统电气性能的前提,对长大隧道区段牵引网电气参数计算方法需要特殊考虑。Tylavsky[15]提出四周无限圆形隧道模型:圆形隧道四周为具有同一电阻率ρ和磁导率μ并向无限远处延伸的大地(见图3)。
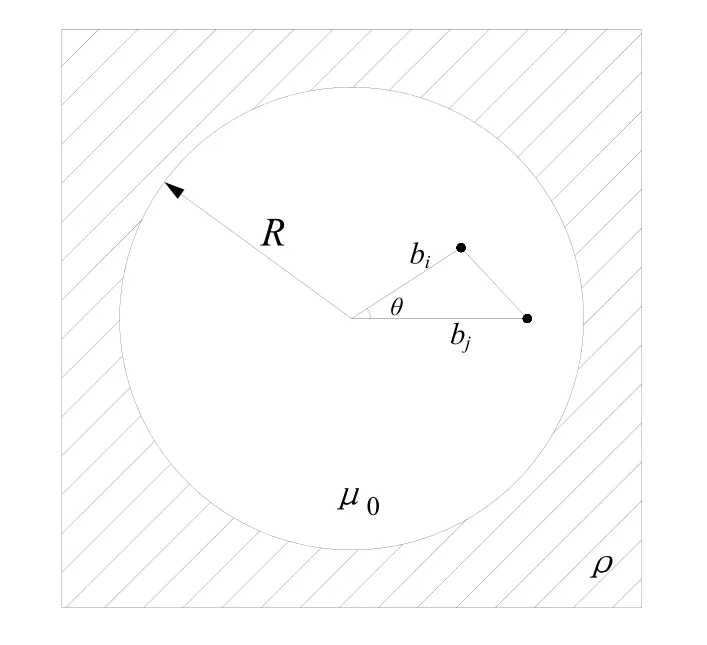
图3 四周无限圆形隧道内导线分布示意图
在工频条件下,平行导体数为m的牵引网中,沿传输线方向单位长压降与传输线电流满足:

式中:Ui为导线i的对地电位,V;Ii为流经导线i的电流,A;Zii为导线i的单位自阻抗,Ω/km;Zij为导线i、j间的单位互阻抗,Ω/km。式(1)可写为:

Z即为导线间单位串联阻抗矩阵。平行导体数为m的牵引网中,导线i的对地电位Ui与线电荷密度qi满足:

式中:pii为导线i的自电位系数;pij为导线i、j间的互电位系数。利用静电场镜像法可得到导线的自电位系数及导线间的互电位系数为[16]:

式中:ε0为真空介电常数;R为隧道截面半径,m;r为导线半径,m;bi、bj为导线与圆心距离,m;bij为2导线间距离,m;θ为2导线对圆心夹角。由式(3)可得电容矩阵:
式中:f为频率,Hz。
Tylavsky以矢量磁势的波动方程为出发点,提出隧道中导线自阻抗、互阻抗计算公式[17],考虑μr=1的条件下公式可简化为:
式中:ri为导线自电阻,Ω/km;ω为角频率,rad/s;μ0为真空磁导率,H/m;p为复数深度,ρ为土壤电阻率,Ω·m。
实际隧道内牵引网各导线空间分布见图4,将实际隧道截面按等周长原则等效为圆形截面,其等效圆半径为3.80 m,各导线距等效圆心距离见表1,牵引网导线参数见表2。
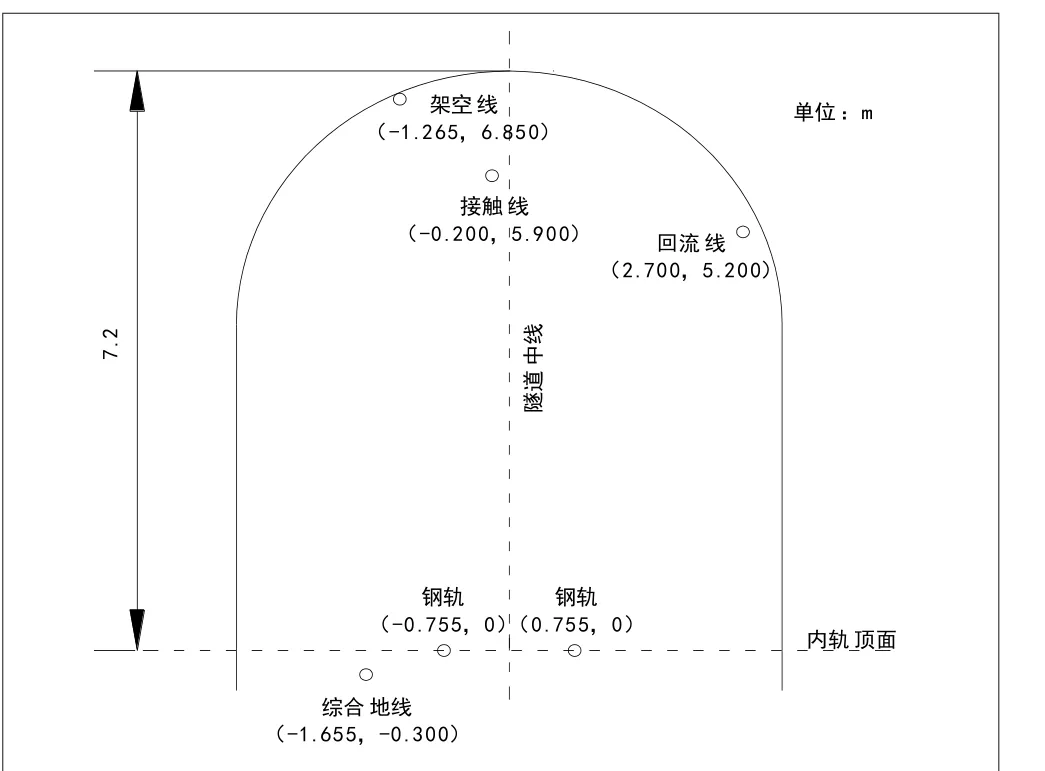
图4 隧道内牵引网各导线空间分布
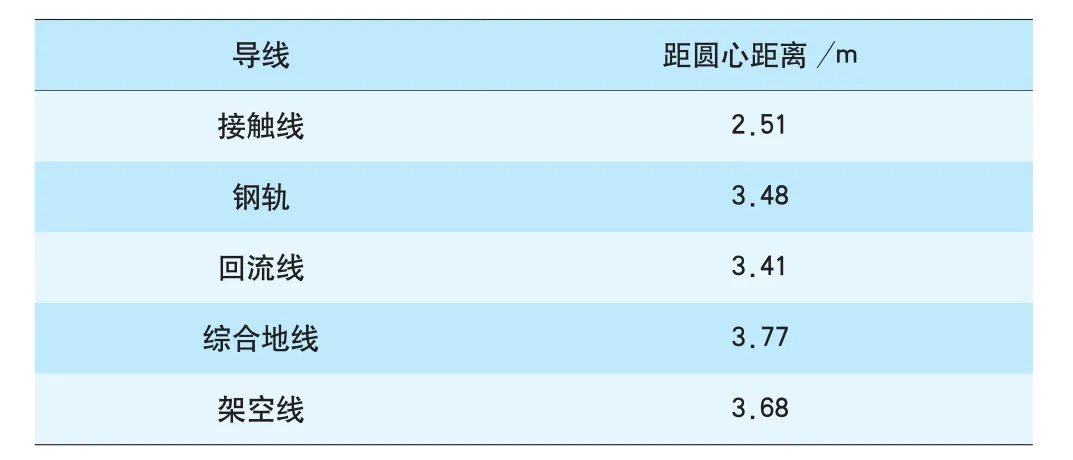
表1 牵引网导线距等效圆心距离
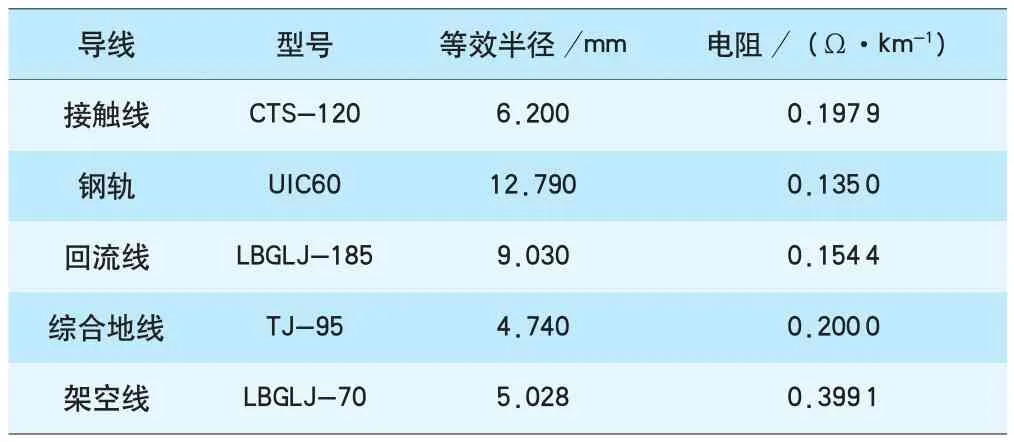
表2 牵引网导线参数
依据上述导线的空间分布与实际参数,利用Tylavsky公式计算牵引网阻抗矩阵参数,计算结果见表3。
3 隧道区段牵引供电系统建模仿真
基于Matlab/Simulink仿真平台建立牵引供电系统仿真模型,其基本条件如下:采用带回流线的单线直接供电方式,接触网采用刚性悬挂,供电区间长度为30 km,牵引变压器为三相V/v接线,额定容量为25 MVA。依据山岭地区土壤电阻率典型值取100 Ω·m,取一般无砟轨道钢轨对地电阻典型值100 Ω·km,机车功率为7 200 kW。牵引网子网每0.25 km封装成1个仿真模块,每个模块的综合地线接地电阻取3 Ω,2条钢轨按照等效合并原则并为1条。隧道区段牵引供电系统仿真模型见图5。

表3 隧道区段牵引网阻抗矩阵参数

图5 隧道区段牵引供电系统仿真模型
仿真模型中考虑无综合接地系统与设有综合接地系统2种条件,机车起始位置距变电所0.25 km,每间隔0.25 km改变1次机车位置进行仿真计算。仿真模型中钢轨间隔2.5 km与回流线钢轨横连,间隔1.5 km与综合地线横连,同时架空线间隔0.5 km与综合地线横连。
4 隧道内牵引回流分布特性
通过仿真计算,有、无综合接地系统2种条件下,当机车以恒定功率运行时机车位置处钢轨电流最大值分布情况见图6,在设置综合接地系统后隧道区段单机车运行过程中钢轨电流超过150 A的比例从60.8%下降到29.2%,钢轨电流的波动幅度同样明显减少,钢轨电流值为56~217 A。由于牵引回流在横向连接处会重新分配,当未设置综合接地系统时,在回流线与钢轨横向连接处钢轨电流大幅度降低;当设有综合接地系统时,由于在回流线的基础上增设了综合地线和架空线2条回流通路,在回流线、综合地线与钢轨横连处钢轨电流均明显降低。

图6 机车所在位置钢轨电流分布
实际工程中,隧道区段牵引回流系统设置综合接地系统后,机车位置处牵引电流随机车位置变化在各回流路径内的分布情况见图7。机车处于不同回流路径的并联点时,经过钢轨回流的电流分配比例显著降低:若机车位于回流线与钢轨横连处,牵引回流在回流线分配比例约占30%,在钢轨的分配比例占42%~55%;若机车位于综合地线与钢轨横连处,牵引回流在综合地线和架空线上的分配分别约占20%、30%,在钢轨的分配比例占22%~39%。机车位于隧道内典型位置处牵引回流分布情况见表4。

图7 机车所在位置牵引回流分布
在设置综合接地系统后,机车运行时钢轨电位同样得到有效降低。有、无综合接地系统2种条件下机车位置处钢轨电位分布情况见图8,在设置综合接地系统后,机车运行时钢轨电位最大值为57 V。综合接地系统对钢轨电位的钳制作用其根本原因是增大了钢轨对地漏泄电导。由于增设综合接地系统使得牵引回流系统由钢轨、回流线、综合地线及架空线4条并联线组成,各导线间每间隔一定距离进行横向连接,使得等效钢轨的自阻抗减小,同时综合地线需要保证良好接地,使得等效钢轨对地漏泄电导进一步增大,其特性阻抗较设置综合接地系统前明显减小,因此机车运行引起的钢轨电位抬升得到有效抑制。
由于隧道封闭环境使得土壤电阻率对钢轨电位的影响甚小,在设置综合接地系统后,钢轨与综合地线的横向连接间距是影响钢轨电位的重要因素。
在模型中考虑钢轨与综合地线的不同横连间距时,假定机车位于隧道内距变电所16 km处,仿真计算隧道区段钢轨电位分布情况,钢轨电位极大值出现在变电所处及机车位置处(见表5)。钢轨电位极大值随综合地线与钢轨横连间距减小而逐渐降低,在满足经济性要求下适当减小横连间距可有效降低钢轨电位。
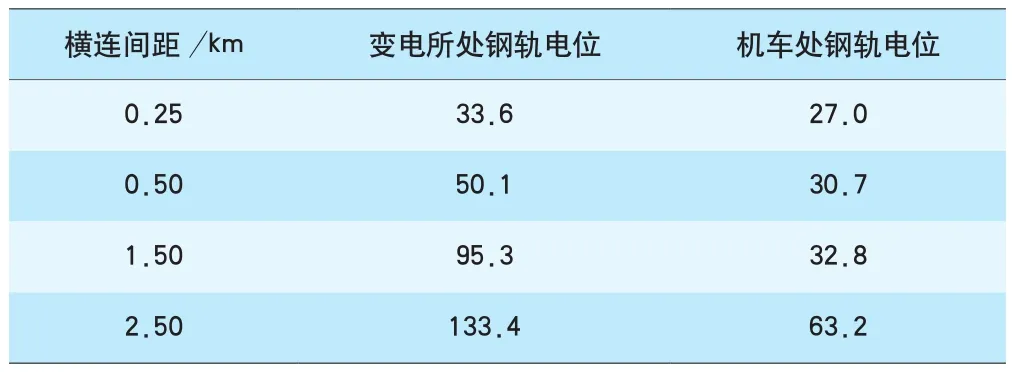
表5 综合地线与钢轨不同横连间距下钢轨电位极大值 V
5 结论
对刚性悬挂接触网方式下牵引网导线参数进行计算,建立电气化铁路长大隧道区段牵引供电系统仿真模型,为隧道区段牵引回流系统的设计提供参考依据,并得出以下结论:
(1)综合接地系统能有效降低隧道区段钢轨电位的抬升,对于线路较长的供电区间综合接地系统的抑制作用越为明显。同时通过减小钢轨与综合地线横连间距可作为进一步降低隧道区段钢轨电位的有效措施。
(2)设置综合接地系统使牵引回流系统形成多线并联的金属性回流通路,有效改善机车运行时牵引回流分布,使经过钢轨上的回流分配比显著减少,尤其当机车位于钢轨与回流线、综合地线横连处,经过回流线、综合地线及架空线的总回流比例将超过45%。

