多股票组合有效前沿的确定——利用Excel求解

(广西大学商学院 广西 南宁 530000)

一、引言

马科维茨投资组合理论模型也称为马科维茨的均值-方差组合模型(Markowitz Mean-Variance Model),该理论模型为分散资产提供理论依据，使人们在理论上对分散资产可以有效降低风险形成系统化的认识，并且该理论模型已广泛应用到各资产类型的投资组合最优配置分析活动中。在实际应用中，马科维茨投资组合理论也存在一定的局限性。技术方面，马科维茨投资组合模型需要大量的基本数据，并且由于模型的运用过程中所需要用到的协方差矩阵的计算工具多、计算量过大,导致期望的估计值存在误差，会使得模型求解存在一些不稳定性，虽然如此，但在发达的金融市场中，该模型已被证明是行之有效的，马科维茨投资组合理论在资产投资组合理论中仍占据重要位置。现本文以2001年到2016年189个月股票市场中的任意具有相关关系或无相关关系的10支股票的交易数据来分析了解多个股票如何进行有效组合,计算出各股票在达到最佳组合时所占的比例，以求得到更具普遍性和广泛性的结论。

二、股票组合有效前沿的研究背景

美国经济学家Markowitz于1952年发表《投资组合的选择》，标志着金融学的“大爆炸”开始产生，他将数理统计方法应用于资产组合选择的研究中，Markowitz的理论也被誉为“20世纪华尔街的第一次革命”!国外特别是发达国家股票市场发展相对成熟，在投资组合研究方面出现了不少学术大亨及丰富的研究成果，其研究可追溯到二十世纪五六十年代，研究方法方面：如Tobin(1958)提出的“二基金分离定理”；Hicks(1962)的“组合投资的纯理论”;Wiliam.F.Sharpe(1963)的“单一指数模型”；Sharpe(1964)、Mossin(1966)等人提出各自的资本资产定价模型(CAPM)等理论极大地丰富了投资组合的研究领域。应用范围方面：Branson(1968)利用马科维茨—托宾资产选择模型来研究本国与国外资产配置问题；Lakonishok等人(1997)将股票分为价值型和成长型投资组合，分别研究了这两种投资组合的业绩表现。投资组合不仅不应用于资本市场中的股票、证券等产品,还可应用到货币市场、黄金市场、房地产市场等投资市场，Harris C.Friedman(1971)将与投资组合理论应用于房地产中，研究结果表明，所建立的选择普通股组合的模型可适用于房地产投资组合的选择。

国内对股票组合的研究始于1990年，相比国外而言起步很晚，到2000年才逐渐利用有效前沿方法来研究股票组合。近年来国内股票市场呈现出起步晚，发展迅速的态势，用了20多年的时间走过了西方国家200多年的历程，但快速发展的同时也带来不少问题，其中之一就是对股票市场的整体性学术研究匮乏。在CNKI中以股票组合有效前沿为主题进行检索，并对检索结果进行计量可视化分析，从总体发文量趋势结果可以发现，国内对股票组合有效前沿的研究比较少而且研究热情也不稳定。从检索文献内容来看，研究主要集中在应用Markowitz均值-方差组合模型和CVaR条件风险价值约束下的均值-方差组合模型来对股票投资组合选择进行分析，可见，目前我国的研究主要是借鉴发达国家的经验方法。在理论上对股票市场进行研究，不管是对投资者还是管理者都有利于加深对股票市场的认知，投资者还可以规避不必要的风险。因此说国内对股票市场的研究还有待进一步提高。

图1 股票组合有效前沿发文量的总体趋势和关键词共现网络图

三、样本确定及参数说明

(一)样本确定及参数选择

每个股民都有自己的喜好、偏好，因此本文选择任意股票市场中不能直接判断他们之间有无相关关系的10支股票(s1，s2……s10)的每个月的收盘价(pit，i=1,2……10;t=1,2……N;N为样本时限内月份数,这里N=189)作为研究对象。股票的选取覆盖了地产、商业、建筑业、工业等多个行业，综合了多个方面选取了10支股票(详见表1),因其涉及范围广及无目的性的选择使结论更具普遍性。综合上文对股票组合有效前沿的背景分析，本文选择时间范围是从2001年1月到2016年11月共189个月。数据来源：通达信数据库。

表1 10支股票详情

四、过程计算与结果分析

(一)过程计算

1.基础计算

(1)模型中用到的其中一个参数是无风险收益率rf,根据我国当前金融市场的实际情况,将一年期定期储蓄存款利率1.75%折算成无风险月收益率,即rf=1.75%÷12≈ 0.15%。

(2)第i支股票在第t月的收益率为下一期的收盘价减当期收盘价除以当期收盘价，公式为rit=pit+1/pit-1(t=1，2，…，N；i=1，2，…，10;N=188)，pit表示第 i 支股票在第 t 月的收盘价。此步骤结束后t=1，2，…，N-1。

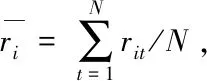
(二)有效前沿曲线图的绘制

(3)绘制前沿曲线:前沿组合1为(σx，Ex)，前沿组合2为(σy，Ey)，计算两个前沿组合在不同投资比例下，如-30%……0，10%……60%，组合的期望收益和标准差，以此绘制前沿曲线。

(4)绘制资本市场线：令c=rf，通过1.2的1)和2)步骤可计算得出市场组合的期望收益Ep、标准差σp和投资比例矩阵p。无风险股票(0,rf)和市场组合(σp，Ep)之间的连线，即资本市场线。得到的无风险资产及市场组合的标准差及期望值分别是：无风险资产的标准差等于0，期望收益等于0.0015；市场组合的标准差等于0.0954，期望收益等于0.0156。

最后由3)的结果绘制前沿曲线图，由4)中(0,0.0015)和(0.0954,0.0156)这两点绘制资本市场线，结果如图2：

图2 有效前沿曲线及资本市场线

在满足相同风险水平下，投资者选择最大收益率的组合；对于相同预期收益率下，投资者选择风险最小的组合这两个条件的投资组合集称为有效前沿。绿色直线的下部分为无效投资部分，就是说投资者在同一风险下会选择高收益的组合，所以投资者不会选择绿色直线的下部分无效率的蓝色曲线，因此上半部分的蓝色曲线为有效前沿曲线，红色直线及其延伸是资本市场线。两条线相交于(0.0954,0.0156)点。

(三)结果分析

投资者关心投资收益率，也关心投资风险，有效前沿曲线描绘了投资组合的风险与收益的最优配置。M是资本市场线与有效前沿曲线的切点组合,与此同时也是市场组合，M点坐标为(0.0954,0.0156),在此点上本文中选择的十个股票的最优组合投资比例为(0.424717,-0.10671，0.197821，-0.05167，-0.01455，0.079364，0.086014，0.319436，0.165343，-0.09977)(记为p，负值表示可卖空)，也就是说在房地产-万科、银行-平安银行、石油-华锦股份、煤炭-冀中能源、旅游-华侨城、酒店-华天酒店、建筑-神州长城、建材-金圆股份、环保-南华生物、钢铁-鞍钢股份这十支股票中，投资者以投资比例p 的组合形式来对这十支股票进行分资投资，以获取最大收益或最小风险。从结果中也可以发现，最优组合的投资比例与市场组合的投资比例完全一致，进一步印证了在市场处于均衡状态时，最优组合等于市场组合。

五、结论总结

股票投资组合是为了减小风险而对各股票进行合理搭配。投资者熟知“鸡蛋不能放在一个篮子里”的风险观念，因此采取分散投资的方法，将资金合理的分散投入若干股票以此来规避风险。不同投资者对股票有不同的喜好，本文简单介绍了面对多个股票时如何利用Excel软件进行最优的资产配置的探究分析，在综合多个市场选取了10支股票作为基础数据，应用马科维茨投资组合模型方法，计算出这10支股票的最优组合投资比例，并且印证了在市场处于均衡状态时，最优组合等于市场组合的结论。不足之处在于未能分析股票个数与风险之间的关系，未能确定最优组合的股票个数。

【注释】

①需要数据结果请联系作者。

②Excel中MMULT函数返回两数组矩阵乘积，MINVERSE函数返回数组的矩阵的逆矩阵。注意的一点是必须同时按Ctrl+Shift+Enter才会出准确的结果。