正定矩阵的判定及应用
(成都理工大学 四川 成都 610059)
矩阵不仅是数学研究的分支和高等代数的主要研究对象,还是理学研究中不可缺少的具有实用价值的工具。矩阵已经成为了处理有限空间和数量关系的重要的工具。正定矩阵在矩阵的研究中占有十分重要的地位,对于正定矩阵的研究有利于我们日后更加详尽的研究二次型、线性空间和线性变换。
一、正定矩阵的定义

二、判定
(一)利用定义判定
利用定义证明矩阵A正定需要证明:对任何的非零实列向量X,XTAX>0.
例设A是m×n矩阵,B=λE+ATA,证明当λ>0时,B是正定矩阵。
证明因为BT=(λE+ATA)T=λE+ATA=B,故B是n阶实对称矩阵,对于任意的n维实向量x≠0,有
xTBx=λxTx+xTATAx=λxTx+(Ax)TAx=λ‖x‖2+‖Ax‖2
由于x≠0,λ>0,则恒有λ‖x‖2>0,而λ‖x‖2≥0,因此xTBx>0(∀x≠0),由定义可得B是正定矩阵。
(二)利用顺序主子式判定
n阶实对称矩阵A是正定的充要条件是A的顺序主子式都大于零,所以我们可以利用顺序主子式来判定一个矩阵是否是正定矩阵。
运用顺序主子式判定矩阵是否正定,首先我们需要确定矩阵的各阶顺序主子式较容易得到,然后根据矩阵的各阶顺序主子式均大于零,可以快速的判断出矩阵是否为正定矩阵。此方法只适用于各阶顺序主子式方便计算的矩阵,具有一定的局限性。
(三)利用特征值判定
运用特征值判定正定矩阵,首先要计算出矩阵的所有特征值,如果所有的特征值都为正数则该矩阵为正定矩阵。如果可以保证所有的特征值全部为正数,那么也可不计算特征值的具体数值直接判定。此方法适用于根据已知可以容易判断特征值是否全为正数的矩阵。
(四)总结
正定矩阵首先必然为实对称矩阵。因此在判定一个矩阵是否正定时必须首先判定该矩阵是否为对称阵,若它不是对称阵,那么其一定不是正定矩阵,若是对称阵则可以继续判定。若给出的是一个具体数字的实对称矩阵,那么在判定时可以验证各阶顺序主子式是否全大于零;若给出的是一个抽象矩阵,那么在判定时可以利用定义或者特征值来进行判定。
三、正定矩阵在广义积分计算中的应用
积分上下限皆为无穷的N重广义积分,传统的积分方法对这类积分往往难以奏效,本节介绍一种利用二次型理论计算这类广义积分的方法。
考虑如下形式的n重广义积分
(1)
其中f(x1,x2,…,xn)是二次多项式,为简单起见,我们可以设f(x1,x2,…,xn)是一个n元二次齐次式(借助于正交变换,总可以化成此类情况的计算)。于是我们只需考虑如下形式的n重广义积分:
(2)
这里f(x1,x2,…,xn)=XTAX是一个实二次型,X=(x1,x2,…,xn)T,A是该实二次型的矩阵。当A是正定矩阵时,上述积分(2)的计算已得到解决:
(3)
但当A是非正定矩阵时,上述积分是发散的,从而可将结果合并表示为:
(4)
现先将(4)式两个结果一起证明如下:
这里λ1,λ2,…,λn是A的特征值,从而A=PTΛP,于是
又由于P是正交矩阵,从而在正交变换X=PY下,体积元素dx1dx2…dxn可以用体积元素dy1dy2…dyn代替,于是(4)中的积分变为:
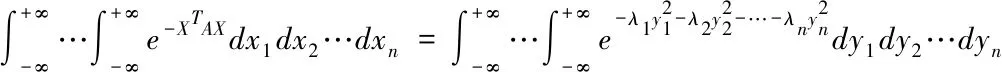
(5)


