多重同步压缩变换及其在模拟地震记录中的应用

(成都理工大学 四川 成都 610059)

一、研究背景

作为处理非平稳信号方法的重要组成部分，时频分析是现代信号处理的研究热点之一，其清楚地描述了信号的频率随时间变化的关系。2018年，于刚等人提出了一种时频分析方法-多重同步压缩变换(MSST)。此方法首先通过严格的数学理论推导，将短时傅里叶变换(STFT)结果在一定频率范围内的时频能量“压缩”到信号的中心频率附近，得到同步压缩变换(SST)的结果；紧接着对SST结果继续进行多次同步压缩操作，以此迭代操作来达到提高时频分辨率的目的。另外作者将此方法运用于通过数值检验和故障震动信号，实验结果证实了MSST的有效性。为了考查其是否能运用于地震信号领域，本文接下来尝试将此方法运用于地震信号处理中，并检验其适用性。

二、多重同步压缩变换

N重同步压缩变换表达式如下：

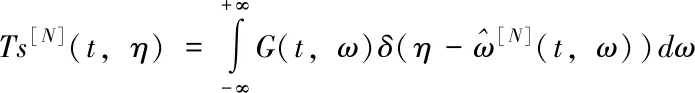
(1)

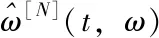
(2)

其中φ(t)是被处理信号的相位。

三、处理模拟地震记录

为了探究MSST在地震信号处理中的适用性，同时为实际数据的处理提供有力的参考依据，本文设计了一个模拟地震记录来分析MSST的时频表征能力，并将处理结果与短时傅里叶变换处理结果进行对比。

在能量衰减与干扰波的影响忽略不计的情况下，地震反射波记录可认为是地震子波与地震反射系数褶积而成。本文采用Ricker子波模型为

RicWave(t)=[1-2(πfmt)2]e(-(πfmt)2)

(3)

其中子波的主频率fm本文分别取30Hz与40Hz。下图1是本文设置的6个反射系数，在0.51s附近的两个反射系数大小相同且距离较近。此模拟地震记录的采样时间间隔是0.001s。图2是模拟地震记录的时域波形图，对其用MSST进行时频分析，得到的结果如图3所示。

从图3、图4可以发现，虽然STFT处理得到的时频谱也能看出反射层大概位置，但是其模态混叠较为严重，特别地，在0.51S附近的两个地层交错在一起；相比而言MSST方法处理得到的时频谱具有较好的时频分辨率，能准确地刻画出反射地层所处位置，分辨率也很好，且在0.51s处的两个地层也得到了较好的反映，并没有因两个地层太近而产生模态混叠的情况。

图1 反射系数

图2 模拟地震信号

图3 STFT时频谱

图4 MSST时频谱

四、结论

为了验证同步压缩变换是否适用于地震信号处理，本文设计了一个模拟地震记录来进行研究。从处理的结果可以发现，此方法能很好地对模拟地震记录进行刻画，且得到的时频分辨率高。这个实验为MSST方法进一步运用于地震实际数据提供了有力的参考。