基于BP 神经网络法的某公路隧道涌水量研究

文旭卿 胡赤兵 郑会康 王昭根

(1.江西交通咨询有限公司，江西南昌 330008; 2.江西省高速集团南昌西管理中心，江西南昌 330100)

1 概述

21世纪以来，经济蓬勃发展，为了满足日益增长的运输需求，交通需要更加的快速与便利，公路隧道建设进入高速发展的时期。公路隧道施工过程中，对隧道涌水量进行合理的预测关系到施工安全以及工程质量，同时也是指导施工的重要依据［1］。本文基于BP神经网络原理，为了预测隧道建设出现涌水的涌水量，建立了公路隧道涌水量预测模型，可以根据预测结果提前采取相关措施。

2 BP神经网络模型

BP人工神经网络是一种具有较强的联想记忆以及推广能力的反馈式全连接多层神经网络。神经网络示意图如图1所示。标准BP神经网络模型由三部分组成(输入层、隐层和输出层)。BP模型输入层的输入和输出满足Oj=Xj。输出层和隐层满足下列等式:

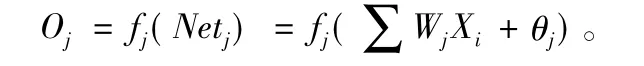
其中，fj为神经元j对应的激发函数;现在使用次数最高的是Sigmoid函数:

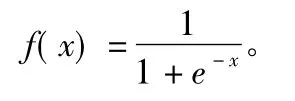
其中，θj为神经元j的阈值;Xi为对神经元j的各个输入;Wj为该神经元j与其对应输入的连接权值。

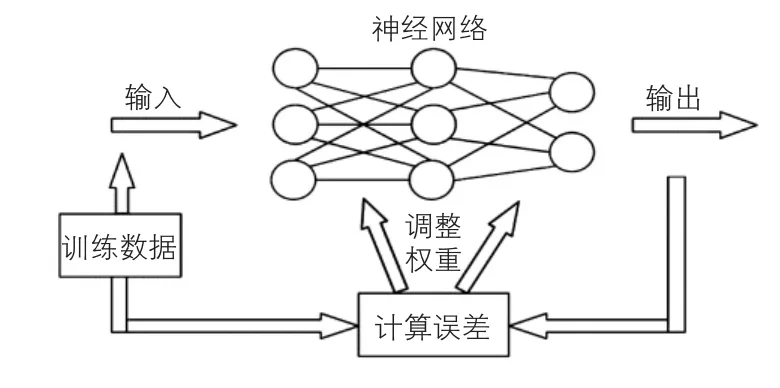
图1 神经网络示意图

BP网络信息储存主要依赖于体系结构和相邻层节点之间的连接权值。体系结构包含网络的输出层，输入层，隐含层的节点个数。把学习率η、隐含层的节点个数、系统误差ε作为结构的主要参数。其中系统应用控制输入层输出层节点个数，用户凭经验控制隐含层节点个数。一般来说学习率取0.01～0.9之间，训练次数和学习率大小成反比。但是，如果学习率太大，会影响网络结构的稳定性。拟定误差ε由输出结果的要求控制，ε越小，要求的精度越高。

BP神经网络算法的具体步骤如下:1)确定神经网络的输入向量X以及目标输出向量T，同时将网络权值初始化;2)进行神经网络实际输出计算;3)进行实际输出向量和符合要求的目标输出值的误差计算;4)不断进行权值学习，直至误差到最小值。

重复上述流程，把系统误差控制到最小。

3 工程应用

3.1 工程概况

本论文所研究的隧道是江西省境内某隧道，其所在区地势整体南高北低，由西南向东北倾斜，成坐南朝北斜坡，垂直高差变幅较大，区内最高海拔712.10 m，最低海拔142.3 m，相对高差一般为60 m～150 m。标段线路经过复杂的地貌，包括山间凹地、剥蚀构造低山、冲洪积沟谷、丘陵等。地表水方面隧址区水系属于赣江水系，地表水较不发育。地下水主要有风化带孔隙裂隙水，基岩裂隙水以及构造裂隙水。

3.2 评价指标

通过分析隧道区域的地质信息及参考前人做过的研究和相关文献，选择地质构造、渗透率、降水量和水头高度作为评价因子。其中将地质构造，依据发育程度和产状的区别，分成5个等级，并对等级进行量化评定，如表1所示。

表1 地质构造量化等级

3.3 BP神经网络学习样本

根据实际现场考察和整理，同时考虑到样本选取典型且全面，选取20个不同的有代表性的洞段的相关参数作为样本，如表2所示。

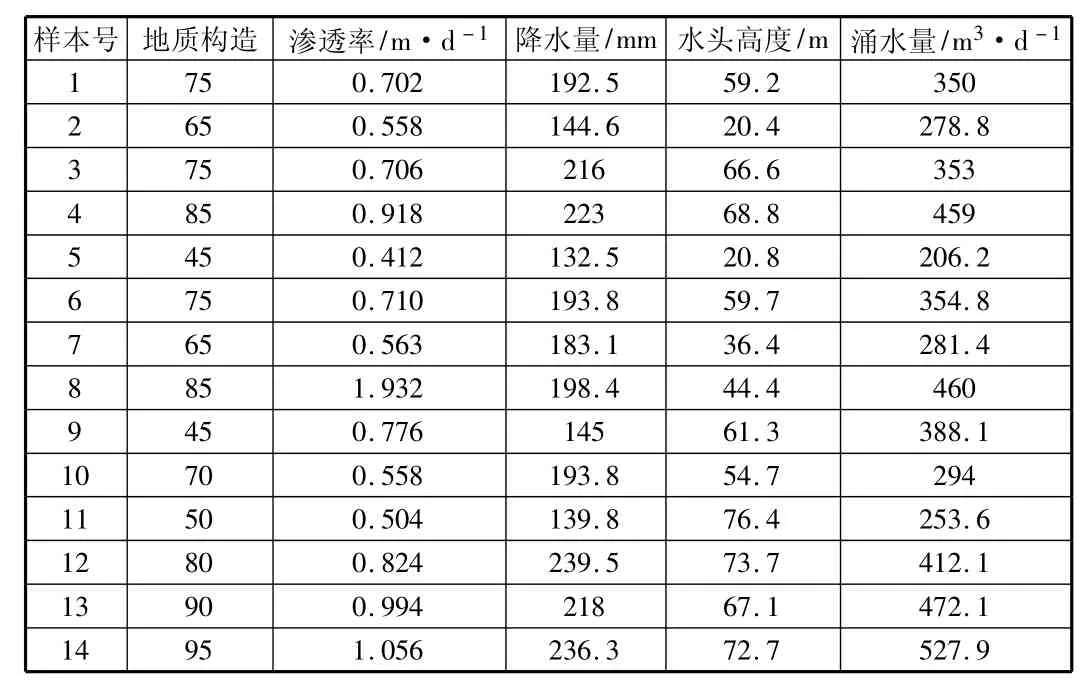
表2 隧道涌水研究样本

3.4 BP神经网络模型

利用BP神经网络对样本进行学习，输入节点为上述四个指标，输出节点为涌水量值，隐含层节点控制在9个。考虑到量纲问题，为了保证不干扰网络的收敛速度和训练模型的可靠性，公式如下:

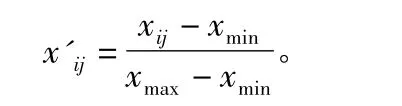
其中，xij为第i项指标第j个数据;xmax，xmin分别为原始数据中的最大值、最小值，归一化后的值介于0～1之间。

经过对前8个具有代表性的样本训练学习，模型误差在第78 213次学习后小于0.02，证明所建网络模型收敛。

3.5 神经网络模型检验

为了保证神经网络的有效性和可行性，对后6个样本进行检验，结果如表3所示。预测结果表明，BP神经网络模型预测值与实测涌水量很接近，其中，相对误差范围在0.825% ～9.66%之间，平均为3.8%，是被允许的误差值范围;结果表明，利用BP神经网络预测模型预测涌水量精度高，有一定的实用价值。

表3 利用BP神经网络模型预测涌水量与实测涌水量的比较

4 结语

选取地质构造、渗透率、降水量和水头高度作为评价因子，基于BP神经网络提出了公路隧道涌水量预测模型，通过与工程实例对比表明，利用BP神经网络模型对隧道内发生的涌水量进行预测是比较准确的。