边坡降雨入渗与坡面径流耦合数学模型及有限元模拟

宋秋明

(湖北省地质勘察基础工程有限公司，武汉 430070)

0 引 言

边坡岩土体的强度和受力与渗流场密切相关，因此边坡渗流分析是其稳定性评价的基础。在降雨,特别是强降雨条件下，边坡渗流与坡面径流过程相互影响，十分复杂。坡面径流分析还可为坡地产汇流、水土保持等分析提供依据。

边坡非饱和渗流过程可采用Richards方程[1]描述；坡面径流过程可采用运动波方程或扩散波方程[2]描述。边坡渗流场和径流场之间，在边坡表面存在一定的流量交换(其值等于入渗率)，是求解两场的必需参数。目前研究中，依据对入渗率处理方式的不同，可大体分为两种方法。第一种采用迭代方法求解入渗率[3-5]。基本思路是先假定一个入渗率，以此为边界分别求解两场，然后根据计算结果基于达西定律更新入渗率后再求解两场，如此循环计算；以前后两次计算是否足够接近为依据结束迭代。迭代法计算量较大，而且入渗率计算的精度往往较差，因此这种方法计算效率较低。第二种方法则设法消去入渗率[6-9]。具体做法是，把离散后的两场方程组(例如有限元格式的离散方程组)相加消去交换流量。这种方法的优点是可以避免计算入渗率；缺点是离散后的方程组系数矩阵不再正定对称，给线性方程组的求解带来不便。

目前研究中，还未见同时描述边坡渗流和径流过程的数学方程。因此，本文将基于径流控制方程和非饱和渗流控制方程，构建同时描述边坡渗流和径流的积分弱解格式的数学方程；然后实现数学方程的有限元模拟；最后通过算例验证数值模拟程序的正确性。

1 问题描述及基本理论

1.1 边坡几何模型

本文分析的边坡几何模型如图1所示。其中x为水平方向坐标，y为竖直向上坐标，x′为沿坡面向下的坐标，α为坡表AB的倾角。简单起见，假设边坡土体均质且各向同性；对边坡渗流而言，只考虑边界AB的降雨，其它边界不透水，忽略源汇项；对坡面径流而言，只考虑降雨和垂直坡面的入渗。

图1 几何模型Figure 1 Geometric model

1.2 非饱和渗流控制方程

边坡非饱和渗流过程采用基于质量守恒和达西定律的Richards方程[1]：

(1)

式中，H为总水头，是位置和时间的函数。H=y+h，

y为位置势；非饱和时h为基质吸力，饱和时为压力水头。C=∂θ/∂h，为容水度。t为时间。K为土体渗透系数。

初始条件为：H(x,y,0)=H0(x,y) 。在边界AB(记为Γq)上：

(2)

式中，n为垂直于坡面的内法线单位向量。nx和ny分别为n在x和y轴方向的投影，其中nx=cosα，ny=sinα。i为垂直于坡面的入渗率，指向坡体内。

1.3 坡面径流控制方程

采用运动波模型描述坡表AB的径流过程，包括连续性方程：

(3)

以及运动方程：

(4)

式中，h′为垂直于坡面方向的水深。q为单宽流量。R为竖直方向的降雨强度。nman为坡面糙率。

初始时刻坡面无径流；径流上游边界(分水岭处)水深一直为0。

2 降雨入渗与坡面径流耦合模型

(5)

根据格林公式：

(6)

(7)

将式(6)、(7)代入(5)：

(8)

(9)

式中，ΓH为定水头边界。在该边界上，限制v=0，则式(9)可进一步简化为：

(10)

式(10)即为式(1)的积分弱解形式。然后将运动波方程融入到式(10)。根据式(4)由链式求导法则有：

(11)

(12)

将式(12)代入到(10)，有：

(13)

考虑到运动波方程适用于描述缓坡的径流过程，因此边坡倾角α一般较小。此时坡面的竖直水深与垂直水深近似相等，即：

h≈h′

(14)

同时由于边坡位置不随时间变化，故：

(15)

将式(14)和(15)代入式(13)得：

(16)

式(16)即为同时描述边坡渗流和径流的积分弱解格式的数学方程。

采用Galerkin有限元法可实现式(16)的数值求解。将图1所示的边坡求解域划分成有限单元。在某一单元e上，将场函数近似表示为：

H=∑NmHm

(17)

式中，Nm为单元e的形函数。m为单元的节点号，m=1,…,n，n为单元节点号。Hm为节点处的总水头，为待求未知量。

同时令

v=Nj，j=1,…,n

(18)

结合式(17)和(18)，则式(16)在单元e上等价于如下矩阵格式的方程：

(19)

其中，矩阵Ae的元素为

(19a)

矩阵Be的元素为

(19b)

3 算例与讨论

本节利用文献[10]中的试验验证上节所建模型。试验装置如图2所示，T1-T13为土壤水势监测点。试验过程为：将土壤完全饱和后放置24h开始降雨；第一次降雨持续45min，雨强0.69cm/min，降雨完成后放置60min；再进行第二次降雨30min，雨强0.69cm/min。AD、DC不透水；出流口用于排水。

图2 试验装置示意Figure 2 A schematic diagram of test installation

数值模拟的初始条件确定如下：将AB、AD、DC视为不透水边界；BC为排水边界；从土体饱和开始计算24h后的结果作为初始条件。降雨开始后，AB改为降雨边界；其余不变。

排水边界的处理：计算过程中如果边界上的节点压力水头大于0，则改为定水头边界，水头值等于高度。计算参数见表1。

表1 数值模拟参数

图3为部分测点压力水头的模拟值与试验结果对比。可见，数值模拟与试验结果符合较好，表明所编程序能够反映土体降雨入渗的非饱和渗流过程。

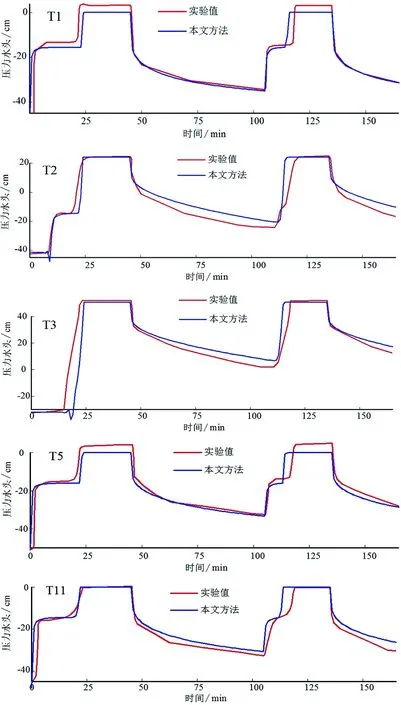
图3 压力水头结果对比Figure 3 Comparison of hydraulic head results

图4为沿坡底各测点压力水头的实验值和模拟值。总体来讲，数值模拟反映出了湿润锋从坡底下侧向坡底上侧推进的过程。

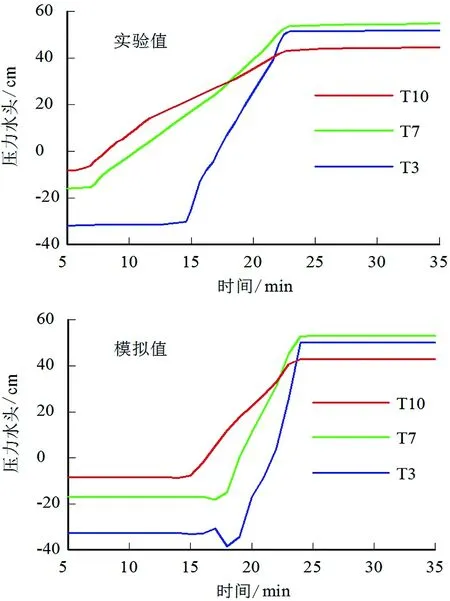
图4 坡底各点压力水头变化Figure 4 Hydraulic head variation of slope base points

当然，数值模拟与试验结果也存在一定差异：如图3中，在第一次降雨时，模拟所得T1和T5在饱和后压力水头较试验结果偏低，这是由于模拟时降雨边界处理方式导致。图4中模拟结果较实验值滞后，主要原因是数值模拟采用的非饱和土渗透参数与实际土体存在一定偏差，特别是在土体较干时，误差较大，是目前非饱和土渗透模型存在的共同问题。此外，当土体接近饱和状态时，数值模拟结果有数值震荡；例如图3中测点T2在10min时、T3在20min时，均有此现象，这可能跟数值计算程序中的迭代方式有关，迭代中渗透系数取值无法匹配迅速变化的渗流场，将在后续研究中进一步改进迭代方法。

4 结论

本文构建了同时描述边坡渗流和径流的积分弱解格式的数学方程。采用Galerkin有限元法实现数学方程的有限元模拟。算例表明，所建有限元模拟方法可用于模拟降雨时的边坡渗流和坡面径流过程。