分析全球副高指数与苏北地区降水关系

周 威 曹春泉 王 岩

（江苏省淮沭新河管理处，江苏 淮安 223001）

1 研究的目的和背景

我国的降水在苏北和苏南地区也存在一定的差异，长系列径流实测资料更有利于准确地探寻随机水文现象统计规律。本文选取1961年到1997年的4月和5月的平均降水资料，分析了苏北地区的降水及其规律的变化，通过数据处理分析和建立相关的水文预报模型确定苏北地区的降水分布特征及其降水规律。

2 苏北地区降水概况

苏北地区一般4、5月份进入雨季，一直到9、10月份。苏北地区多年平均降雨量达到800～1 000 mm，其中在汛期占比偏大，但是苏北地区数量库容有限，上游来水也是丰枯不均，总的来说，苏北地区水资源相对比较紧缺。

3 计算步骤

3.1 建立标准化的正规方程组

假设预报因子X是由m个组成，每个因子的长度为n；预报对象y，其长度为n。在逐步回归中采用的是国土调查逐渐标准化的正规回归方程组：

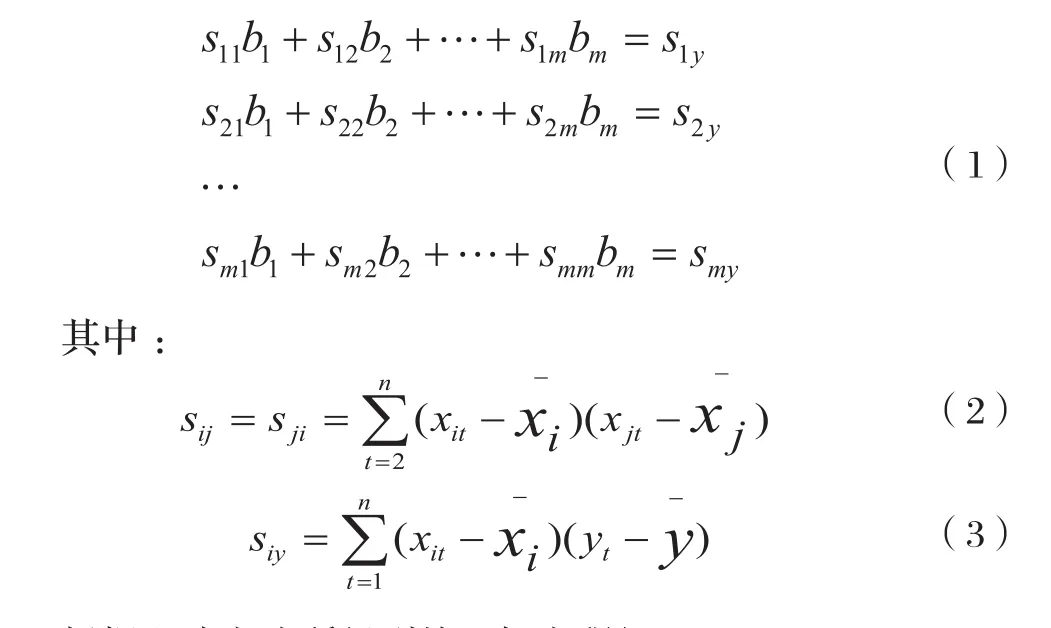
根据上述方法所得到的正规方程组：

回归系数bi是相应的预报因子的系数，但各个因子的单位不一样，为消除单位的影响，引入标准回归系数的概念。对式进行变换。

令：

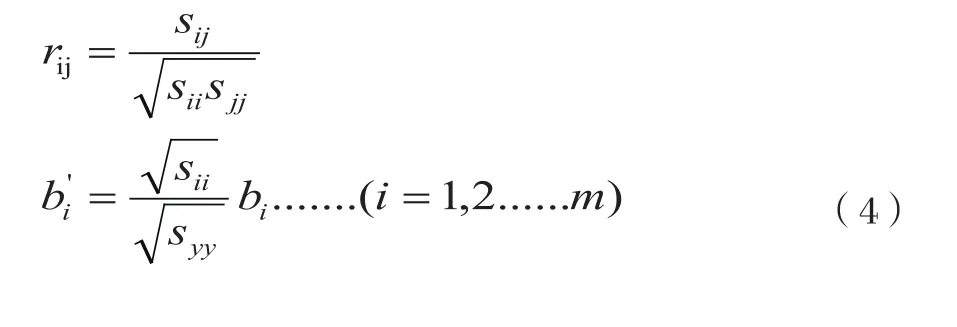
有如下关于bi’的相关矩阵方程组：

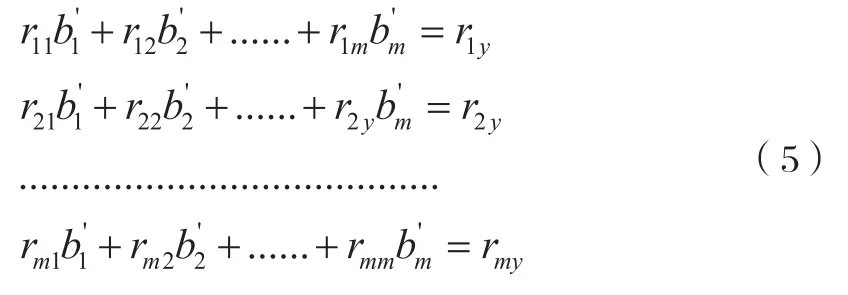
方程组关于标准化回归系数的标准化正规方程组，其中的回归系数bi’与x及y所取的单位无关。称为标准回归系数。

相应的增广矩阵：

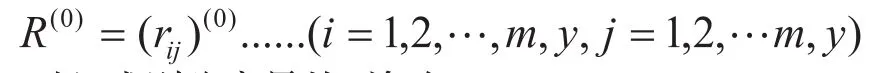
3.2 引入或剔除变量的F检验

（1） 定义方差比 ：

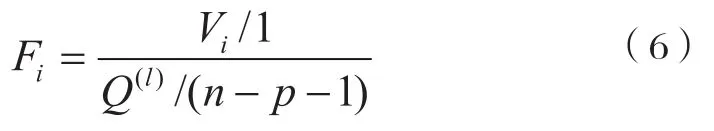
给定自由度 （1，n-p-1），信度α查表得Fα，若Fi＞Fα拒绝原假设，xi作用显著，可以引进xi。

若Fi≤Fα接受原假设，xi作用不显著，要剔除xi。

（2） 剔除因子 ：

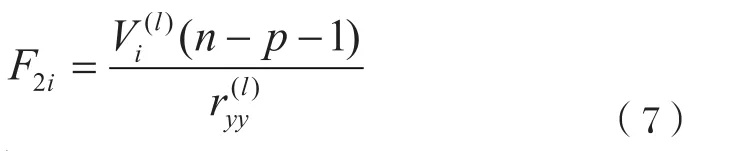
当F2i≤Fα时，剔除因子。

（3） 引入因子 ：

引进因子公式：

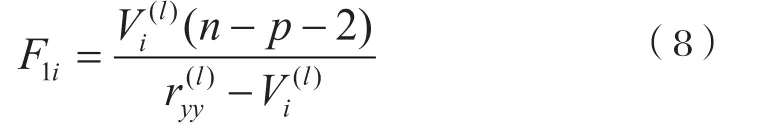
给定信度α，自由度 （n-p-2） 查表得Fα值，当F1i＞Fα时引进因子。

（4） 标准回归方程：

（5） 回归方程 ：

代入关系式：

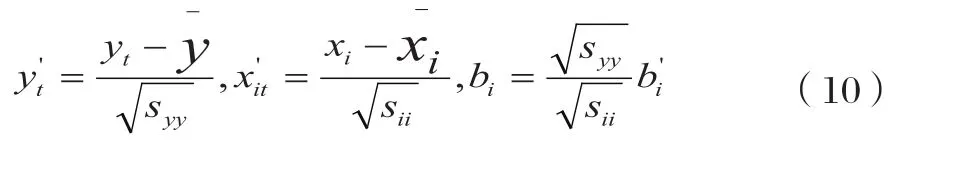
得回归方程：

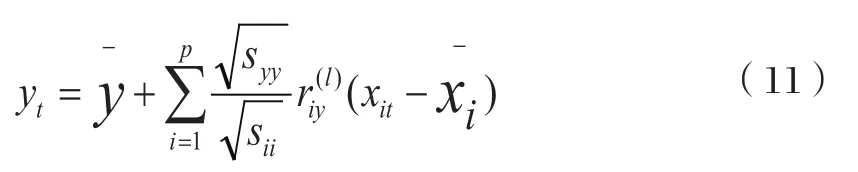
4 回归效果的检验

利用逐步回归分析所得到的优势因子计算其复相关系数和剩余标准差sy，对回归方程回归效果进行检验。

（1） 复相关系数 ：

R成为复相关系数，由它来衡量回归效果的好坏，0≤R≤1，复相关系数R＞Rα，则回归效果就好。

（2） 剩余标准差 ：

剩余标准差sy可作为衡量回归效果和预报精度的标志。若sy愈小，则回归方程来预报y的值就愈精确。

5 结果分析

根据已有的降雨资料和降雨资料数据处理分析及其变化规律，并且从中挑选出相关性大的影响因子然后利用编写好的程序得出预报方程的系数，建立预报模型并根据此模型对1961～1997年的苏北地区4月份和5月份平均降雨量进行预报。

5.1 建立预报模型

首先使用单相关系数计算方法，从83项大气环流因子中挑选出部分与预报对象相关性较高的因子，在本节中预报因子是提前1年来挑选的（ 即预报对象的序列为1953～2008年，预报因子序列为1952～2007年），挑选因子的显著性水平信度a为0.01时通过单相关系数检验可以初选出15个大气环流因子，而信度a为0.05时通过但相关系数检验可以初步选出33个大气环流因子。

5.2 实验结论分析

本次研究的是全球副高指数与苏北地区降水的关系分析，通过本次课设对相关数据的实测值处理分析得到了该地区4月份和5月份的平均降水，然后通过多元回归分析、逐步回归分析和M-K突变检验的方法处理分析，通过相关模型得出一些相应的结论：首先，通过在因子表中筛选出3组因子，通过相关系数法和给定的逐步回归和多元回归辅助程序得到相关趋势图。通过单相关系数法和逐步回归给定的程序，得到拟合期的误差范围是0.142 873 061，实验期的误差范围是0.080 938 452，属于允许误差范围，符合标准。

6 结语

本次主要是进行数据的处理与计算，通过逐步回归的方法去分析和处理数据，最后得出拟和曲线图，探究全球副高指数与苏北地区降水的关系。