改进的Canny算子在靶场光学数据处理中的应用
高 燕,侯艳杰,夏 霏
(太原卫星发射中心,山西 太原 030027)
0 引言
靶场外测事后数据处理系统担负着飞行试验结束后,通过对外测系统的原始测量信息进行整理、加工、扣除系统误差及减少随机误差,得到用户所需飞行器外弹道参数及弹道参数精度的职能。光学事后数据处理主要是利用光电经纬仪拍摄的光学图像,通过人工判读得到测元信息,进行2站或多站交汇弹道解算。
光电经纬仪在跟踪飞行目标的过程中,由于随动系统动态滞后及操作等原因,使视轴(主光轴)偏离目标一定角度,产生脱靶量,或称为跟踪误差[1]。由于设备内部安装反射镜片,在跟踪拍摄时,转动镜头造成反射片挤压变形,发生位置移动,造成光轴中心偏移。进行脱靶量修正不足以抵消设备十字丝中心偏移对弹道解算产生的影响,因此在试验任务中需要对光十字丝进行修正,提高弹道解算精度。
杜飞明等人提出的十字丝综合检测方法[2],计算量小,方便可行,已经稳定应用于在线测试,但是对于消除假十字丝的方法还有待进一步简化;李立春等人提出的基于随机Hough变换(RHT)[3]的十字丝自动检测算法,对十字丝目标的灰度、大小和形状变化具有鲁棒性,从而能够快速识别十字丝目标,但是该算法需要满足4条十字丝识别准则才能进行,大大限制了算法应用的范围;曾接贤等人提出的基于格式塔完形规则的闭合轮廓提取方法[4],融入显著性约束和折线逼近边缘拟合算法,减少背景边缘和噪声对算法的影响,通过分析边缘间的闭合关系与区域的显著性,得到最终闭合轮廓。该算法虽然能有效提高边缘提取的准确性,但是对边缘显著性存在一定的依赖,不利于工程实际应用。
结合工程实际,利用改进的Canny算子进行边缘检测,提取出十字丝边缘,由于十字丝宽幅较大,提取边缘较为粗糙,因此运用自适应的迭代阈值分割技术进行直线提取,为获得十字丝中心点位置坐标,使用加权整体最小二乘法,通过对拟合方程联立方程组求解,得到交点坐标[5]。本文提出的基于改进的Canny算子的边缘提取算法对光十字丝进行修正,提高了弹道解算精度。
1 传统Canny算子
Canny算子的基本思想是对初始图像采用高斯函数进行平滑滤波,然后进行图像梯度计算,利用一阶微分极大值提取图像边缘点,同时由二阶导数的零值交点确定图像的强边缘和弱边缘,最后通过设置高低检验阈值对图像进行强边缘和弱边缘检测[6-7]。Canny边缘检测算法流程如图1所示。

图1 Canny边缘检测算法流程
1.1 高斯平滑滤波
设二维高斯函数为:
(1)
对原始图像F(x,y)进行卷积得到平滑处理后的图像I(x,y)为:
I(x,y)=G(x,y)·F(x,y),
(2)
式中,符号·表示卷积。
1.2 计算图像梯度
采用2×2邻域内一阶偏导数有限差分计算I(x,y)的梯度幅值和梯度方向,将点(x,y)在x方向和y方向的一阶偏导数分别记为Kx(x,y),Ky(x,y),
(3)
则有梯度幅值为:
(4)
梯度方向为:
θ(x,y)=arctan(Kx(x,y)/Ky(x,y))。
(5)
1.3 梯度幅值非极大值抑制
若像素点(x,y)的梯度幅值M(x,y)大于或等于沿梯度方向θ(x,y)两个相邻像素点的梯度幅值,则判定该点为可能的边缘点[7]。
1.4 双阈值检测和边缘联通
对经过非极大值抑制的图像设置高、低2个阈值,大于高阈值的认为是强边缘点,小于高阈值但大于低阈值的认为是弱边缘点,小于低阈值的点直接剔除,分割得到两阈值边缘图像T1[x,y],T2[x,y]。T1[x,y]由高阈值得到,理论上不含假边缘,但在轮廓上可能存在间断。双阈值算法的目的就是要在T1[x,y]中把边缘连接成轮廓,达到轮廓端点时,采用低阈值得到的边缘图像T2[x,y]的8邻域位置寻找可进行轮廓连接的边缘,反复使用T2[x,y]进行边缘搜索,直至将所有T1[x,y]的间隙连接完成[8]。
2 改进的Canny算子
传统Canny算子采用在2×2邻域内进行有限差分求梯度,由于对噪声过于敏感,易出现误判的假边缘和丢失部分真边缘的问题,导致边缘检测不准[8-10]。
常见3×3邻域的4邻点梯度公式为:
(6)
计算45°方向导数
K45°(i,j)=G(i-1,j+1)-G(i+1,j-1)。
(7)
计算135°方向导数:
K135°(i,j)=G(i+1,j+1)-G(i-1,j-1)。
(8)
计算水平方向差分:
K0°(i,j)=Kx(i,j)+(K45°(i,j)+K135°(i,j))/2。
(9)
计算垂直方向差分:
K90°(i,j)=Ky(i,j)+(K45°(i,j)+K135°(i,j))/2。
(10)
针对45°,135°旋转可变性的缺点,采用改进水平和垂直方向差分[11]的公式为:
(11)
(12)
改进的梯度幅值为:
(13)
3 自适应迭代阈值分割技术
阈值的选取直接影响边缘检测算子的效果,本文采用自适应的迭代阈值分割技术,其基本思想是选择图像灰度的中值作为初始阈值T0,将图像分割为2个区域,分别计算这2个区域的灰度均值μ1,μ2,利用μ1,μ2计算新的阈值Ti+1,计算Ti+1,Ti的差值,小于某一给定值迭代终止[12]:
(14)
4 加权整体最小二乘法
假设最小二乘模型为:
y+ey=(A+EA)ξ,
(15)
式中,y为N×1维观测值;A为N×q维的真实系数矩阵;ey,EA为对应的随机误差矩阵,ey~N(0,σ02Qy),eA为vec(EA)~N(0,σ02QA),vec表示拉直算子,vec(EA)表示按列拉伸后的向量;Qy,QA为矩阵y,A的协方差矩阵;ξ为q×1维的待估参数。
将ey看作是EA,ξ的非线性函数,将式(15)按照Taylor公式展开并忽略二次以上极小项,式(15)变为:
(ξ0T⊗IN)δeA-y,
(16)
由最小二乘平差问题可知,为保证随机误差最小,式(15)需满足残差向量和权矩阵乘积最小,即满足:
(17)
式中,Py为观测值的权重矩阵;PA为真实系数矩阵的权重矩阵。对目标函数和约束条件构造拉格朗日函数
(ξ0T⊗IN)δeA)。
(18)
对式(18)两边各未知分量求一阶偏导数并令等于零,解得
(19)
式中,
Py=Qy-1,PA=QA-1。
(20)
加权整体最小二乘法间接平差形式迭代求解方法如下:
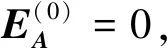

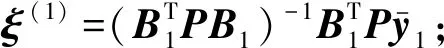
④ 设置迭代终止阈值ε,若满足|ξ(i)-ξ(i-1)|<ε,则迭代终止,否则,转入②;
⑤ 输出最终解ξ。
5 基于融合算法的光十字丝修正
提出的基于改进的Canny算子的边缘提取算法流程如图2所示。

图2 基于改进Canny算子边缘提取算法流程
首先进行边缘检测,运用改进的Canny算子对边缘进行粗提取,由于提取出来的边缘不够精细,因此使用自适应迭代阈值分割技术进行十字丝边缘精确提取,阈值的选择是关键。利用加权整体最小二乘法对十字丝的2条直线进行拟合,目的是计算出直线的交点,即十字丝中心点位置,需要根据中心点位置对设备十字丝进行脱靶量修正。
在靶场试验中,光十字丝图像如图3所示,从图像中可以看出,十字丝中心点位置较为模糊,在实际操作中,需要依靠人眼进行人工判读,其判读结果的准确性与判读人员相关性较大,存在较大的判读误差。采用本文算法对十字丝图像进行精确提取,获得准确的中心点位置,在此基础上进行脱靶量修正,避免人为操作带入的误差。使用本文算法进行十字丝中心提取后的图像如图4所示。

图3 原始光十字丝图像
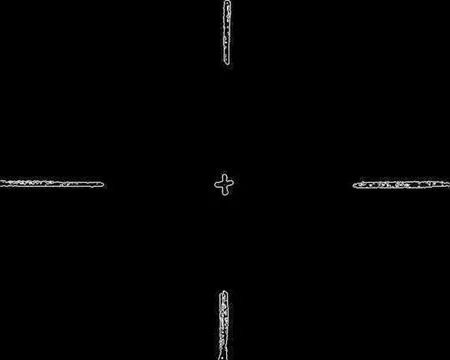
图4 基于改进Canny算子的光十字丝图像
获取十字丝中心点位置后,在拍摄的光学图像中进行脱靶量修正。在画幅上记录的方位角和高低角是胶片坐标原点即主光轴的角坐标αk,γk,它与目标的真实角坐标之间的差就是跟踪误差,记为Δαk,Δγk,有:
(21)
式中,
(22)
式中,f为设备的焦距,计算单位与x,y单位一致。
6 仿真结果分析
仿真实验在Matlab中完成,设置高低阈值分别为255,0,进行边缘粗提取,多测速数据采用仿真数据进行解算。与全局Otsu方法和局部阈值分割方法比较,自适应迭代阈值分割算法选取阈值为0.265 4,图像轮廓更加清晰。加权整体最小二乘法迭代12次终止,输出中心点位置坐标,将得到的中心点位置图片进行脱靶量修正,进行光学弹道解算。
比对实验从光学弹道反算测元与多测速弹道反算测元残差比对、光学部修测元与多测速弹道反算测元残差比对、光学综合弹道与多测速弹道比对、光学综合弹道与多测速弹道位置比对、光学综合弹道与多测速弹道速度比对5个方面,对使用本文算法的光十字丝修正和简单光十字丝修正(即使用肉眼进行十字丝中心判断)效果进行比对,简单修正方法和使用本文提出算法进行光十字丝修正解算出的光学弹道设备反算测元与高精度多测速弹道反算测元的角度残差比对如图5所示,在图5基础上添加部位修正后的效果比对如图6所示,简单修正方法和使用本文算法解算的光学综合弹道与多测速弹道位置比对如图7所示,在图7基础上细化的位置和速度残差比对如图8和图9所示。

图5 2种算法解算光学弹道与多测速弹道反算测元角度残差比对
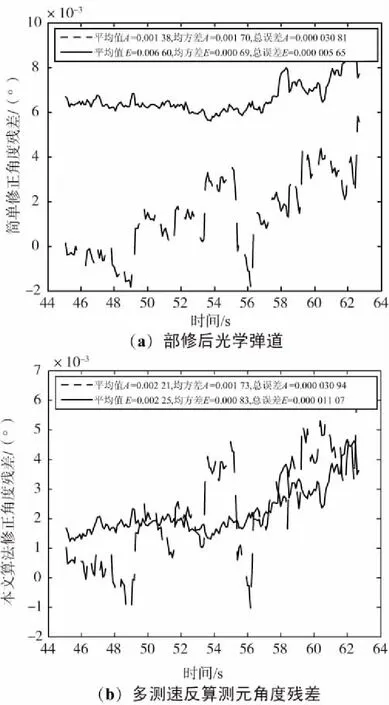
图6 部修后光学弹道与多测速反算测元角度残差比对
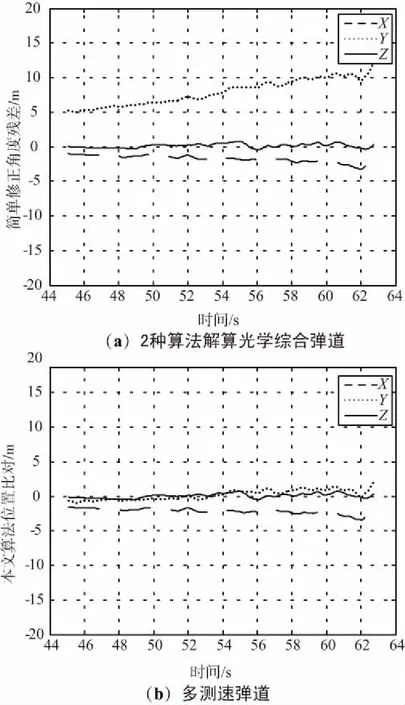
图7 2种算法解算光学综合弹道与多测速弹道比对

图8 2种算法解算光学综合弹道与多测速弹道位置残差比对

图9 2种算法解算光学综合弹道与多测速弹道速度残差比对
从图中可以看出,使用本文算法修正后的光学弹道和简单进行十字丝修正的光学弹道与其他高精度弹道比对,无论是在反算测元测角、位置还是速度,总体精度要更高。
7 结束语
提出的基于改进的Canny算子的边缘提取算法进行光十字丝修正,相对于简单进行十字丝修正的方法,确实能够提高弹道解算精度,同时减少人眼判读识别带来的修正误差。但是由于融合算法计算复杂度相对较高,导致图像判读处理的时间相对增加。今后将在改进阈值分割算法的基础上,不断优化算法,减少算法的时间复杂度,保证在较短时间内,解出高质量弹道。

