极化SAR图像解译中的不相似性度量

潘 婷，杨祥立 ，宋 辉，杨 文

(武汉大学 电子信息学院，湖北 武汉 430072)

0 引言

SAR通过微波成像具有全天时、全天候工作等特点，并能提供大尺度、高分辨率的地表观测数据，其独特的优越性使其在对地观测中发挥着重要作用[1-2]。极化SAR(Polarimetric SAR，PolSAR)系统通过收发不同极化状态下的信号，能够更好地反映散射单元的信息，被广泛应用于环境保护、灾害监测、地形测绘以及城市规划等领域。目前大量的星载、机载极化SAR系统能够持续提供高质量的极化SAR图像用于地面精确观测。

常见的极化SAR图像解译任务包括滤波、目标检测、图像分割、地物分类和变化检测等。在这些任务中，不相似性度量扮演着重要角色。不相似性与相似性是一组相对概念，二者分别从正、反两方面反映待评估样本数据之间的相关性，通常范围在-1～1或者归一化到0～1，本文用不相似性进行统一。许多学者对不相似性度量进行了研究，然而在现有的距离中，没有一种不相似性度量是最优的，也没有一种不相似性度量适合所有极化SAR图像应用。因此，本文旨在分析、归纳目前常用的不相似性度量，并结合极化SAR图像处理的特点，对不相似性度量未来的研究趋势进行了展望。文献[3-4]已对极化SAR数据中常见的不相似性度量进行了一定的总结归纳，本文在其基础上进一步完善与扩展，并对近几年提出的不相似性度量等工作进行了补充。值得注意的是，由于极化协方差矩阵和相干矩阵数据作为极化SAR数据最常用的表达形式，被广泛应用于各种应用中[4]。因此，本文主要探讨和研究基于矩阵表示形式的极化SAR数据之间的不相似性度量。

1 背景知识

1.1 极化SAR数据

对于极化SAR数据而言，散射矩阵描述了一种完全极化的过程，一般只能较好地描述点目标。如果将散射矩阵S看成一个随机变量，为了统计其表征目标的信息，通常会采用一个矢量化操作V(S)将散射矩阵S转换为散射矢量的形式，即等效的四维散射矢量k4：

(1)

(2)

式中，tr(·)为矩阵的迹；T为矢量转置；Φ为一组正交矩阵基。采用不同的矩阵基可以得到不同的矢量表达形式。Lexicographic基和Pauli基是2种常用的矩阵基[4]：

k4L=[SHH，SHV，SVH，SVV]T，

(3)

(4)

假设散射矢量k的维度为d，其等价于系统极化通道数。d=4时为全极化；d=2时为双极化；d=1时为单极化SAR配置[4]。在单基站的情况下，一般假设天线满足互易定理，散射矩阵S的交叉极化分量近似相等，SHV=SVH，此时散射矢量k的维度d=3，记为k3。在Lexicographic基及极化条件下，散射矢量k服从多变量圆复高斯分布，概率密度函数为[1-2]：

(5)

式中，Σ=E{kkH}定义为协方差矩阵；H表示复共轭转置。

假设有L个服从d维复圆高斯分布的独立随机散射矢量样本{k1，…，kL}，满足L>d。由这些散射矢量样本计算得到的协方差矩阵C是非奇异的，定义为：

(6)

在匀质区域，样本协方差矩阵C服从复Wishart分布，其概率密度函数为[1-2]：

(7)

对于复Wishart分布模型，其模型参数为尺度矩阵Σ=E{C}和形状参数L。在SAR图像统计分析问题中，L表示视数，是一个与多视处理有关的量。而在其他背景下，该参数则表示模型的自由度。考虑到视数间并非完全独立，且存在一定的相关性，这一概念通常被等效视数所替代[4]。

1.2 距离测度

在极化SAR图像解译任务中，一个关键的问题是如何选择合适的距离测度来度量样本数据之间的不相似性。协方差矩阵包含了全部极化信息，因此常使用定义在矩阵数据空间上的距离函数来度量矩阵数据之间的不相似性。而不同的距离函数反映了数据不同的性质。按照严格的数学定义，当距离函数满足一定条件时，可被称为距离测度。在数学上，测度(Metric)被定义为集合上X的一个函数(距离)[4]：

d(·)：X×X→。

(8)

且对任意的x，y，z∈X满足下列条件：

①d(x，y)≥0(非负性)；

②d(x，y)=0，当且仅当x=y(同一性)；

③d(x，y)=d(y，x)(对称性)；

④d(x，z)≤d(x，y)+d(y，z)(三角不等式)。

严格意义上，如果一个映射仅仅满足上述前3个性质时，将其称作伪测度(Pseudo Metric)。由于极化SAR数据本身的特点，如几何、统计分布特性等，对其定义的距离往往是非欧氏的，甚至是非测度的；另一方面，在极化SAR数据解译任务中，往往只关心由距离函数计算出的样本数据之间的相似性/不相似性程度，并不要求不相似性度量必须满足数学上定义距离测度的4条性质[4]。

2 极化SAR不相似性度量

2.1 基于特征的不相似性度量

描述2个样本协方差矩阵C之间的差异性最简单的方法是从协方差矩阵中提取典型的实值特征f，并用距离测度函数计算所提取特征之间的不相似性[5]。一般来说，常用的距离函数为[5]：

dfs(Cx，Cy)=f(Cx)-f(Cy)，

(9)

dfa(Cx，Cy)=|f(Cx)-f(Cy)|。

(10)

极化SAR数据中具有代表性的特征ψ有散射总功率(Span)、矩阵特征值(Eigenvalues)、极化散射熵(Polarimetric Entropy，H)、极化各向异性度(Polarimetric Anisotropy，A)、目标随机性(Target Randomness，TR)、极化因子(Polarimetric Factor，PF)和极化不对称性(Polarimetric Asymmetry，PA)等[5]。对于给定的协方差矩阵C=(cij)，1≤i，j≤d做特征值分解[5]：

C=[u1...ud]diag(λ1，...λd)[u1...ud]T，

(11)

式中，ud为特征向量；λd为相对应的特征值，满足λ1≥λ2≥...≥λd，对于单基站的极化数据来说d=3。式(12)～式(18)给出上述几种常见特征的计算方法：

(12)

Eigenvalues：λi，

(13)

(14)

A：(λ2-λ3)/(λ2+λ3)，

(15)

(16)

PF：1-3λ3/(λ1+λ2+λ3)，

(17)

PA：(λ1-λ2)/(λ1+λ2-2λ3)。

(18)

这种基于特征的不相似性度量虽然计算成本低，但是由于没有充分考虑各个极化通道之间的相关性，不能充分挖掘极化SAR数据之间的极化信息，因此，在描述样本数据时，不能较好地描述数据间的差异性，应用效果也一般。

2.2 基于统计分布的不相似性度量

Wishart距离是目前广泛用于分类和分割的一类极化SAR数据距离测度。Lee等人[1-2]最先将Wishart分布引入极化SAR数据分类任务中，提出一种基于最大似然(Maximum Likelihood，ML)的分类器，定义了样本协方差矩阵C到第m个类别中心Σm的距离：

(19)

Wishart距离本质上是描述样本点到集合(类别)中心的距离，结合经典的中心聚类算法，如K-Means等，即可衍生为极化SAR数据中最常用的迭代Wishart分类器。Wishart距离用于地物覆盖分类任务时具有许多优点，例如可用于经过相干滤波的极化SAR数据(独立于视数)；独立于极化基，具有鲁棒性，可扩展到多频极化SAR分类等[1-2]。在Wishart距离的基础上可以进一步定义类内距离和类间距离[6]。目前，迭代Wishart分类器已经成为许多极化SAR数据分类方法中的重要组成部分。

从数学意义上讲，Anfinisen等人[7]指出Wishart距离并不是一个良好的距离测度，因为它不能很好地满足上文定义测度的4个条件。由于Wishart模型属于指数分布模型，其负对数似然可以表示为一个唯一确定的Bregman散度与没有分布参数的函数之和：

-lg(p(Ψ，θ)(x))=dφ(x，μ(θ))-lg(bφ(x))，

(20)

式中，lg(·)为自然对数函数；x为统计量；Ψ为累积量凸函数；θ为自然参数；φ是Ψ的凸共轭函数；μ为期望函数。在复Wishart模型中，Bregman散度可以定义为：

(21)

Anfinisen等人[8]将复Wishart分布中L>d的限制条件去掉，得到了松弛复Wishart分布。Frery等人[9]在此基础上，推导了松弛复Wishart分布之间的4种随机距离。针对异质以及极端异质区域的统计建模问题，有时需要更复杂的模型，例如极化K分布[10-11]、极化G分布[12]和Kummer-U分布[13]等。其中，Kummer-U分布最开始是用于极化向量数据的分割问题建模，Akbari[14]等人将Kummer-U分布推广到复协方差矩阵，也就是Ud分布，多用于多视极化数据中的簇建模。其中Doulgeris等人[15]基于Ud分布，提出了一种自动聚类分割算法。复杂的分布模型往往具有更复杂的密度函数形式，由对应的对数似然函数也可导出相应的极化SAR不相似性度量，然而它们往往形式复杂或者不具有解析的表达形式，限制了其使用场合。

2.3 基于假设检验的不相似性度量

假设检验是统计推断中用于检验统计假设的一种方法，常被用于数学统计与通信信号处理等方面。针对极化SAR变化检测应用，Conradsen[16]等人提出了基于复Wishart分布的假设检验衡量2个协方差矩阵的不相似性度量。假设X，Y为d×d厄米特正定(Hermitian Positive Definite，HPD)矩阵，服从复Wishart分布，即X∈Wc(d，n，Σx)，Y∈Wc(d，m，Σy)。关于它们是否相等的假设检验为：

零假设H0：Σx=Σy，

非零假设H1：Σx≠Σy。

(22)

则最大似然比统计量为[16-17]：

(23)

假设n=m即得到样本协方差矩阵之间的Bartlett距离：

(24)

式中，Σx+y=n/(n+m)Σx+m/(m+n)Σy。

进一步假设Σy已知，则得到修正的Wishart距离：

(25)

(26)

Kersten等人[17]将dB和dRW应用于模糊聚类中。在谱聚类的框架中[7，19]，希望用具有对称性的距离来衡量不相似性。Anfinsen等人[7]讨论了针对极化SAR矩阵数据定义逐对相似度的问题，并将dB和dSRW用于谱聚类中。

除了常用的基于最大似然比假设检验的统计量，Akbari等人[20]基于HLT(Hotelling Lawley Trace)假设检验提出了一种新的统计量。该统计量可用于描述复协方差矩阵之间的差异性，其抽样分布近似于Fisher-Snedecor(FS)分布[20]。Akbari等人[20-21]将这种新的统计量用于极化SAR数据的非监督变化检测中，并取得了不错的实验效果。在基于区域和分层的聚类方法中，需要衡量2个区域或2个类别之间的差异性。根据Conradsen的范式，Cao等人[22]推导了针对2个样本集合间的距离测度，假设其服从具有同样等效视数的复Wishart分布：

(27)

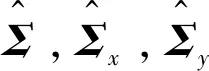
Alonso-Conzàlez等人[26-27]利用极化SAR数据构建二分树(Binary Partition Tree，BPT)的过程中也涉及到比较2个区域的差异性。该不相似性度量与区域的2个因子有关：包含极化信息的协方差矩阵和区域大小。在这种情况下，SRW距离可以写成：

(28)

式中，Σx，Σy为2个区域的协方差矩阵；Nx，Ny为区域大小。

2.4 基于信息论散度的不相似性度量

信息论一般用于研究如何量化数据中的信息，因此基于信息论散度的距离测度被广泛应用于极化SAR数据中。例如，修正的Wishart散度dSRW实际上就是2个服从Wishart分布的协方差矩阵的Kullback-Leibler (KL)距离。Goudail等人[28]利用KL，Bhattacharyya距离来衡量2个服从复圆高斯分布的不相似性。Erten等人[29]利用互信息导出一种距离测度，对时间序列多通道场景之间的相干性进行描述。Frery等人[30]则将h-φ信息散度引入随机距离中，密度函数fX，fY的h-φ散度定义为：

(29)

式中，h：(0，∞)→[0，∞)，φ：(0，∞)→[0，∞)均是严格的单调递增函数，且h(0)=0。当选取合适的h，φ，就会得到一些常用的散度距离，例如KL，Rènyi，Bhattacharyya，Hellinger距离[31]。为了保持测度的对称性，提出了

(30)

通过这种方式推导出来的不相似性度量一般都具有测度的前3个性质，因此由信息论散度导出的极化SAR距离测度在极化SAR图像解译中具有重要作用。

在复Wishart模型的前提下，许多常用的信息论散度可以获得解析的表达式，这对于极化SAR图像处理来说非常有利。结合复Wishart模型与Bregman散度，可以推导出不同情况下具有解析表达式的极化SAR不相似性度量。对于复杂场景，还可以考虑用混合Wishart模型建模。然而在描述混合Wishart模型之间的差异性时，一些常用的信息论散度是不存在解析解的，如KL散度。而柯西-施瓦茨(Cauchy-Schwarz，CS)散度[32]以及total平方欧式(tSL)散度对于混合Wishart模型则存在解析解。宋、杨等人[4，33]给出了混合Wishart模型下，CS散度以及tSL散度[34]的具体表达式，并将其应用于地物分类以及变化检测等应用中，取得了不错的实验效果。

除了常见的几种信息论散度之外，文献[31]基于Hölder散度以及Hölder伪散度[35]的定义推导了在复Wishart分布下，2个样本协方差矩阵之间的不相似性度量HPDW(Hölder Pseudo Divergence for Wishart)以及HDW(Hölder Divergence for Wishart)，并用于监督和非监督分类等应用中，取得了不错的分类效果。在复Wishart分布下，不同参数的选取，HPDW以及HDW等价于一些常见的不相似性度量，如Chernoff距离和Bartlett距离。

2.5 基于信息几何的不相似性度量

除了前面几种定义不相似性的方法之外，也可以通过用测地距离来定义矩阵的不相似性。常规的距离测度都是针对欧氏空间中的矢量数据的，因此一种简单的处理方法是将样本协方差/相干矩阵矢量化。然而Kersten等人[17]认为欧氏距离并没有考虑协方差/相干矩阵的非欧氏几何特性，并用实验证明其在滤波、分类等应用中效果较差。由于协方差/相干矩阵位于HPD矩阵组成的锥体中，该锥体空间具有黎曼流形结构，简单的矩阵矢量化忽略了其几何性质。然而定义在流形上的距离测度却能够有效地描述矩阵的空间几何性质，尽管这一类距离测度都是定义在实数空间上的，但是很容易被推广到复数域[25， 36]。D’Hondt等人[25]提出考虑2种黎曼流形距离测度，分别为仿射不变黎曼测度(Affinity Invariant Riemannian Metric，AIRM)和对数欧氏黎曼测度(Log-Eu-lidean Riemannian Metric，LERM)：

(31)

dLE(Σx，Σy)=‖lg(Σx)-lg(Σy)‖F，

(32)

式中，lg(·)表示矩阵对数；‖·‖F表示Frobenius范数。

AIRM是目前应用最为广泛的黎曼流形测度，它刻画了流形上2个点间的测地线距离。AIRM对于矩阵逆及相似变换具有不变性。然而其计算涉及到特征值分解以及矩阵对数运算，具有较高的计算复杂度。LERM作为AIRM的一种替代方案，仍然保留了AIRM 的一些性质(如对求逆和相似性变换保持不变)，实际上采用了一种映射方法：将不平坦的黎曼流形上的点映射到平坦的欧氏空间。JBLD(Jensen-Bregman LogDet Divergence)是AIRM的一种替代方案。JBLD除了保有AIRM的一些性质外，还能更有效地衡量相似性[18，37]。Alonso-Gonzales等人[27]在BPT构建的框架下运用了不同的距离测度，实验结果证明黎曼距离拥有最好的结果。

除了上面几种常见的定义在流形上的距离测度之外，Wasserstein距离也定义在流形上。p-Wasserstein距离是一种基于最优传输理论定义的距离测度，当p=1时，是常见的地球移动距离；p=2时，Wasserstein距离是一种黎曼流形测度，在流形空间描述2个概率分布之间的测地线度量。文献[31]利用复散射矢量服从复高斯分布的性质，推导了适用于复高斯分布的Wasserstein距离，并用于监督和非监督分类等极化SAR数据应用中。对于服从复高斯分布的散射矢量kx～N(0，Σx)，ky～N(0，Σy)，二者之间的Wasserstein距离为：

dWG(kx，ky)=tr(Σx+Σy-2(Σx1/2ΣyΣx1/2)1/2)，

(33)

式中，tr(·)为求矩阵的迹。dWG虽然描述的是2个复散射矢量之间的差异性，但实际上参与计算的只有协方差矩阵，因此也可以间接看作是描述2个样本协方差矩阵之间的不相似性。

2.6 其他不相似性度量

前面提到的距离测度都是针对正定矩阵(满秩)的，只有在此情况下矩阵求逆和对数行列式值运算才有效。对于充分多视的极化数据可保证满足这一要求。然而在很多应用中，极化数据通常是未经过充分多视、甚至是单视的，此时上述距离测度均无法使用。考虑到这一点，Alonso-González等人[26]提出了只利用协方差矩阵对角元素的距离测度，并运用于基于BPT的极化SAR滤波框架中。这些距离测度对于反映各个通道之间的相关性的非对角元素不敏感。仅仅考虑协方差矩阵的对角元素，不仅可以确保矩阵的满秩，而且避免了矩阵正则化时的滤波操作[27]。一般情况下，基于对角元素定义的不相似性度量会假设协方差矩阵的非对角元素为0。常见的对角不相似性度量有：

对角修正Wishart距离：

(34)

对角测地线距离：

(35)

对角相对归一化距离：

(36)

对角相对距离：

(37)

除了极化SAR数据的协方差矩阵，通过极化数据、极化目标相干/非相干推导出的极化特征向量对极化SAR数据处理也很重要。对于这些特征向量，常用的不相似性距离包括欧氏距离、余弦距离和马氏距离等。对于极化SAR数据来说，一种常用的欧式距离是基于不同极化通道信号强度定义的[1-2]：

(38)

然而，式(38)定义的距离并没有将各个极化通道之间的相关性考虑进去，因此，Hu等人[38]提出了一种考虑协方差矩阵中所有元素的欧式距离：

(39)

由于极化SAR图像固有的成像机制，基于区域的统计分布特征可能比单个像素的矢量特征更好地描述极化SAR数据。因此作为经验特征分布的非参数估计，基于特征直方图的距离测度也很有用。这些距离测度包括Minkowski距离测度、直方图交集(Histogram Intersection，HI)距离测度、 Kolmogorov-Smirnov (KS)距离测度、X2统计距离测度等。

3 不相似性度量的发展趋势及展望

结合极化SAR图像处理问题的特点，对不相似性度量未来的发展趋势进行如下展望：

① 对于不同的任务，如极化SAR图像的分割或分类。极化SAR图像的处理通常包括3种不同类型的距离测度计算：像素点与像素点之间、像素点与区域(如超像素块)之间和区域集与区域集之间。找到或定义一个对于上述3种类型都适用的、鲁棒的距离测度是十分必要的。

② 对于时间序列的极化SAR图像滤波、分类和变化检测任务，为了更好地分析多时相极化SAR数据，需要提出一种新的不相似性度量，能够一次性计算多幅极化SAR图像。

③目前的不相似性度量大多建立在复Wishart分布的基础上。复Wishart分布主要用于描述基于高斯分布的多视极化SAR数据。然而在高分辨率极化SAR数据中，非高斯模型往往能够提供更好的性能。因此需要研究基于不同分布(例如K，G0分布)情况下的不相似性度量[39]。

④ 针对不同的任务，人为设定的距离测度往往不能满足所有需要，且对于数据的改变不鲁棒。因此在极化大数据时代，希望能够借助测度学习自动地选取最好的不相似性度量[26，40-44]。根据不同的极化SAR图像处理需求自动学习距离函数，可以考虑基于深度学习网络去学习一个距离函数。

4 结束语

不相似性度量在极化SAR图像解译任务中扮演着十分重要的角色，是极化SAR遥感邻域的研究热点。本文从多个角度出发，对经典的及近几年来提出的极化SAR不相似性度量进行了归纳与总结。随着极化SAR大数据时代的到来，基于深度学习的不相似性度量将会是下一个研究热点。