基于自适应目标融合技术的指挥控制系统研究
张梦骏,郑益凯,朱 恺,陈天群,魏兵卓
(上海机电工程研究所,上海 201109)
0 引言
新形势下,防空武器系统面临着防御各种导弹、预警机、隐身飞机和无人机等越来越多新型武器的硬杀伤威胁,同时面临防御电磁干扰、网络攻击等软杀伤武器威胁,单一的目标探测传感器已经不能满足对复杂战场环境感知的需求,迫切需要利用多传感器对战场环境进行多方位、多角度感知,再进行态势融合[1],从而快速、准确和连续地对威胁目标进行跟踪、识别和打击等[2]。
数据融合技术在20世纪70年代出现于美国,首先在声呐侦察潜艇中提出了数据融合,随后美国在90年代投入了大量资金开展了研究,取得了飞速发展。我国起步较晚,20世纪80年代开始了相关技术研究,90年代初,出现了较多的理论研究成果,90年代中期出现了一批有初步融合能力的多传感器融合系统。但是,总体而言,大部分融合系统存在融合准确性低、融合精度差和抗干扰能力差的问题。
针对多部多种雷达、光电跟踪设备协同作战,各传感器探测精度不同,且传感器自身在实际环境中受各种因素干扰影响测量数据精度[3-4]等的问题,为指控系统设计了一种自适应多源数据融合技术,通过探测信息系统的时空采样,对目标进行检测、关联和自适应融合等多级多功能处理,提高系统空间和时间的精度范围,增加系统的利用率,提高系统目标探测识别能力,为指挥员提供有用的决策信息[5-6]。
本融合算法通过内插外推法进行高实时性时间配准;通过UT变换技术[7]进行空间对准,控制了变换中的误差;通过简单加权法与滑窗判决逻辑结合的方式进行航迹关联;改进了传统融合算法,通过计算某一传感器探测数据被系统中其他传感器测量值的综合支持程度确定其权重系数,来提高融合算法的抗干扰能力。
1 时空配准算法
1.1 时间配准
防空武器系统对目标数据的实时性要求较高,时间段内插外推法满足目标实时性要求。
信源的目标航迹序列如图1所示。在t1时刻,只存在信源1的信息,此时不进行外推配准。在t2时刻,信源n得到目标信息,将信源1在t1时刻的信息采用外推法外推到t2时刻,这时,信源1和信源n就可以进行航迹关联处理。在t3时刻,信源2得到目标信息,则将信源1在t1时刻的信息和信源n在t2时刻的信息分别外推到t3点,然后,信源1、信源2以及信源n就可以进行航迹关联处理。

图1 信源的目标航迹序列
这里的外推航迹是与待融合航迹已经相关或者有可能相关的航迹。与之无关航迹不外推。
采用内插外推的方法,将在相同时间段内,由高精度传感器探测到的目标数据推算到低精度传感器探测到的目标数据的时间点上,最终形成多个等间隔的目标探测数据,为融合处理做好准备。
同一时间片内的观测数据常有多个,如图2所示。

图2 时间配准
高精度a向低精度b归结:
速度的外推:假设在同一时间片内,目标做匀速直线运动,则有时间点t1外推至时间点t2速度不变,即Vt1=Vt2。
1.2 空间配准
空间配准是将所有信源的信息转换到同一空间坐标系下,从而实现数据链信息与其他信源信息的融合[8-10]。
由于多载体多传感器探测运动目标时,各传感器存在校准误差、卫星导航系统偏差和环境误差等,而坐标系变换的非线性将导致系统误差无规律地放大或缩小,因此,传统空间配准方法常会出现航迹偏移的情况,降低融合系统性能。UT变换技术能够以EKF的计算量实现强非线性坐标系的精确变换,因此采用UT变换校准技术[11-12]对误差进行有效地控制。

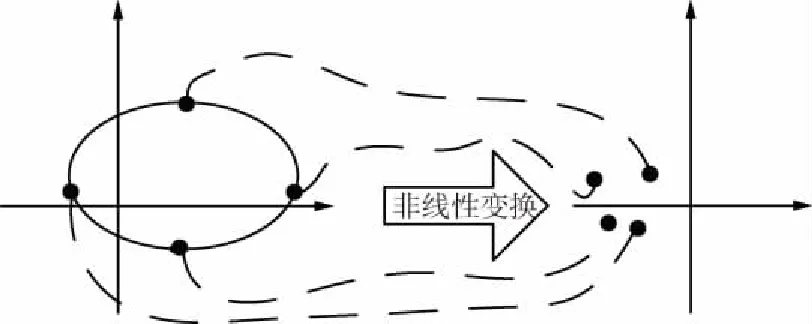
图3 UT变换方法
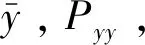
y=f(x)。
UT变换算法框架步骤如下:

② 通过f(·)非线性变换处理输入变量Sigma点集{xi}中的每个Sigma点,从而求得处理后的Sigma点集{yi}。
yi=f(xi),i=1,...,L。
在相关文献[13]中对UT变化的精度给出了具体证明,相比于一阶线性化,UT的精度更为优异。
Sigma点采样策略的选取是UT变换算法最重要的点,其中包括确定Sigma点的数量、位置值和相应的权值。在选取Sigma点时,需要保证其抓住了x最为重要的特征,因此需要满足以下条件:
g[{xi},px(x)]=0,
式中,Px(x)为x的密度函数。
随后,通过c[{xi},px(x)]=0这个代价函数来进一步优化Sigma选取点。通过代价函数,所需要的特征被进一步增强,但同时,也不要求与所引入特征完全一致。采样策略的精度与代价函数值的增加成反比。
通过以上2个函数,就确定了Sigma点选择依据:在g[{xi},px(x)]=0的条件下,最小化c[{xi},px(x)],从而采用对称采样的Sigma点采样策略。
2 航迹关联与融合
本融合算法是一种分布式[14]融合跟踪,分为2个步骤,一是航迹关联,即识别出哪些航迹出自同一批目标;二是融合估计,即对同一目标的不同航迹进行融合处理,求得全局状态估计[15]。
2.1 航迹关联
所谓航迹关联,就是由不同传感器探测到多条航迹时,识别出哪些航迹是出自同一批目标[16]。
在防空指挥控制系统中,各信源提供的是目标航迹信息。一般而言,各子系统并不提供各信源跟踪处理的模型,无法构造互协方差[17],而且在实际系统中,各个融合时刻所利用的信息并不一定固定来源于某一传感器。因此,本算法采用简单加权法处理航迹关联问题,同时,对各个通道进行解耦,实现解耦的简单加权航迹关联算法。简单加权法仅给出一个融合时刻的航迹相关情况,因此将简单加权法与滑窗判决逻辑结合,来确定整个时间序列中航迹相关情况。
首先,对传感器的类型按照状态维数进行分类。然后,针对要判断关联的2个传感器数据按照图4,依照解耦的简单航迹关联算法判断是否关联。

图4 航迹关联判断表(依据不同的状态类型)
根据融合处理的时间设定,周期性地读取航迹数据,对于该周期内的各传感器航迹数据,首先根据航迹时刻排序,对于最新的航迹,按照航迹的新旧逐次处理。对于尚未进行关联判断的航迹,在时间校准后,进行航迹关联的假设判断。对于航迹关联确认的航迹,建立航迹匹配,并启动航迹融合。在完成该航迹融合后,将涉及航迹融合的所有航迹从航迹排序表中删除。然后对剩余航迹中最新航迹重复上述过程实现融合,当航迹融合处理时限到达时,停止融合。
首先引入一些基本表示和描述方法。设局部节点1,2的航迹号集合(即其相应的目标号集合)分别为:
U1={1,2,...,n1},U2={1,2,...,n2}。

设H0和H1是下列事件(i∈U1,j∈U2):


这样航迹关联问题便转换成了假设检验问题。

Cij(l|l)=Etij(l)tij(l)′=

加权法使用的检验统计量是:
当αij(l)小于采用χ2分布得到的某一门限,则认为假设H0是正确的;相反,则认为假设H1才是正确的。在H0中,tij(l)是一个高斯分布,从而可以知道,αij(l)是一个nx自由度的χ2分布。其中,nx代表状态估计向量的维数。采用多拍累积下的加权航迹关联,从而提高同一性识别的稳定性。
2.2 航迹融合
当航迹关联成功后,进行目标的状态估计融合,对各目标的实际位置、速度等参数进行估计。航迹融合主要解决的是在降低探测到目标信息噪声值的条件下一个将来自某一个目标的多个探测信息相互融合。一致性数据融合算法[18]是一种有效的融合算法,通过对各个传感器数值进行比较,建立不同传感器之间测量数据的联系,从而选择进行融合的传感器数据。传统的一致性数据融合算法存在着主观性影响大、易受传感器测量扰动的影响[10],因此在传统方法上进行改进,根据某一传感器测量数据受其他测量值的支持程度确定其权重系数,通过这种自适应的方式,提高融合数据的精度,降低测量扰动影响。
假设有n个传感器测量的航迹关联成功,i传感器的测量值为xi,σi为该传感器的测量精度,则在算法中i传感器测量模型为:
用dij,dji表示传感器i与传感器j测量数据相互之间的支持程度,称为传感器i与传感器j的置信距离。理论上而言,置信距离应该具备对称性,因此,将dij,dji的计算模型定义为:
由上式可以看到,测量精度较低的传感器在求置信距离时其测量值的权重系数较小,测量精度较高传感器测量值的权重系数较高。通过这种方式,来将不同传感器测量精度对置信距离的影响程度显示出来,相比传统直接求算数平均等方法而言,因为考虑到了测量精度的问题,更具备先进性。
从置信距离的求解公式可以看到,dij是一个介于0~1之间的数值,这个值越小,说明传感器i测量数据越被传感器j所支持。
传统方法通过将置信距离与人为定义阈值进行比较的方式,来确定传感器间的支持程度度量r,支持数只能为0或1。这种方式由于阈值确定的主观性存在较大误差,因此,这里定义r的值为:
rij=1-dij,(i,j=1,2,…,n)。
这种直接用置信距离来刻画传感器测量数据间的支持程度,可以规避人为定义阈值带来的误差,同时又能减小扰动因素对融合结果的影响。
求解传感器两两间的支持程度度量数后,所有传感器的支持矩阵可以表示为:
有了传感器支持矩阵,进一步计算传感器i测量值被所有其他传感器测量值综合的支持程度,这里,定义βi为传感器i测量值被所有其他传感器测量综合支持程度。由信息分享原理可知,最优数据融合估计的信息量之和可分解为若干信息量之和,而各信息量具有的全系数应该满足和为1的要求,即:
由概率源合并理论可知,存在p1,p2,…,pn,使得:
βi=p1·ri1+p2·ri2+...+pn·rin,(i=1,2,…,n),
式中,p1≥0,(i=1,2,…,n)。
用矩阵可以表示为:
β=Rn·P,
式中,β=(β1,β2,...,βn)T;P=(P1,P2,...,Pn)T。
支持矩阵Rn是一个非负对称矩阵,根据Perrorr-Frobenius[19]定理,Rn存在最大模特征值λ(λ>0)征值,从而λ对应的特征向量Y=(y1,y2,...,yn)T为正,并满足:
RnY=λY。
由上式可知,λY可以用于表示测量数据的综合支持程度的度量。第k个传感器的综合支持程度可以表示为:
λyk=y1·rk1+y2·rk2+...+yn·rkn,(k=1,2,…,n)。
由上式可知,P就是Y归一化后的结果,所以,令:
αk即为第k个传感器的综合支持程度,多传感器的最终数据融合值可以表示为:
通过这种改进的方式,从而实现航迹的自适应融合。
3 数值仿真计算
3.1 融合算法仿真
通过仿真的方式对整套融合算法的有效性进行验证。通过7个放置于地图上不同探测点的传感器模拟器对同一批目标进行探测(各模拟器在该批目标真实航迹的基础上加上各自不同的噪声),形成7组探测航迹。各传感器模拟器设置参数如表1所示。
表1 传感器模拟器设置参数

模拟器序号数据率/Hz探测参数延迟时间/ms11R,A,E4021/3R,A,E4031/2A,E5041A,E5051R,A3061R,A,E3071R,A,E30
不同传感器模拟器在数据率(探测周期)、探测参数(模拟三坐标雷达、二坐标雷达和光电探测装置)及延迟时间(处理延时、通信延时)不同,各探测传感器将航迹传送给中心指控系统,指控系统融合算法对目标各航迹进行时空配准、航迹关联和航迹融合。图5所示为融合后航迹。从图中可以看到,指控系统接收到来自不同传感器的7个批号的目标,经过融合后只输出了一个目标航迹,表明这7个航迹成功完成了关联,并且数据得到了有效融合。

图5 目标航迹融合
图6所示为目标真实航迹、融合航迹方位角与时间关系图,可以看到,融合后目标方位角与真实目标方位角基本吻合,融合基本有效。最大误差为2.4162°,满足当前一般防空武器系统使用要求,后续还需进一步改进算法来提高融合精度。

图6 目标真实航迹、融合航迹方位角与时间关系
3.2自适应一致性数据融合算法精度计算
通过数值计算的方式验证自适应一致性数据融合算法的有效性。这里引用文献[20]的数据,采用10个传感器对某一值进行测量,传感器参数及测量值如表2所示。
表2 传感器参数及测量值

传感器测量值xi方差值σi2传感器测量值xi方差值σi211.000.0560.650.2520.990.0771.010.1030.980.1081.020.1040.970.2091.030.1050.500.30101.500.30
通过本改进算法,计算出融合值为0.977。认为设置传感器发生扰动,将传感器1的测量值改为1.2,方差值改为0.04。再次进行计算,获得融合值为0.989。扰动前后融合值变化率为1.1%。而采用传统一致性数据融合算法[21]获得的融合值前后变化率为1.24%。可见,自适应一致性数据融合算法具备较强抗干扰能力,有助于提高融合精度。
4 结束语
针对在多防空武器系统进行协同作战情况下,指控系统对三坐标雷达、二坐标雷达和光电探测设备等多类型多个传感器对目标探测后数据融合,提出了一种先进的融合算法。采用时间段内插外推法对目标进行时间配准,采用UT变换校准技术进行空间配准,将简单加权法与滑窗判决逻辑结合进行航迹关联,采用解耦的简单凸组合航迹融合法进行航迹融合,采用改进的一致性数据融合技术完成数据融合。通过仿真对算法进行检验,实现了数据融合工作,且融合数据满足一定精度要求,证明了融合算法的有效性。通过数值计算验证了自适应一致性数据融合算法的先进性。

