矩形薄板的参数共振失稳理论与试验
钟子林,刘爱荣
(广州大学-淡江大学 工程结构灾害与控制联合研究中心,广州 510006)
0 引 言
关于板在动力荷载作用下的稳定性问题已有学者开展研究。Bolotin[1]推导了单边简谐荷载作用下四边简支矩形板的Mathieu-Hill方程,给出了横向位移函数只含单个谐波时的不稳定域解。Ostiguy等[2]推导了周期荷载作用下四边简支矩形板的Mathieu-Hill方程,探讨了长宽比对板动力失稳的影响。Pierre等[3]运用谐波增量平衡法求解出板在有、无阻尼情况下的不稳定域与非线性曲线。Nguyen等[4-5]对4种不同边界条件各向同性矩形板在动力荷载作用下的稳定和非线性振动进行了研究。钟子林等[6]利用伽辽金法将周期荷载作用下的四边简支矩形板的动力控制方程转化为马奇耶方程,运用特征值法求解了板的动力不稳定域和非线性振动曲线并与有限元数值解进行了对比分析,验证了解析解的正确性。Ganapathi等[7]基于位移和应力连续条件,对周期性面内荷载作用下板的非线性不稳定行为进行了研究。Robinson等[8]采用微分求积法求解了平面内运动矩形粘弹性板的凹凸截面微分方程,给出了横截面形状对板的稳定性影响的曲线图,并观察到板的发散失稳。傅衣铭等[9]推导出在纵横周期荷载共同作用下四边简支中厚板的非线性运动控制方程,探讨了板厚、长宽比、纵横周期荷载大小对不稳定域的影响。袁尚平等[10]通过Galerkin法得到四边简支矩形板在周期荷载作用下的非线性动力方程,求解出板在2倍超谐振动下的振幅,并运用仿真模拟的方法讨论了2倍超谐振动对屈曲薄板非线性振动的影响。Minh等[11]对具有中心裂纹的矩形FGM板的稳定性问题进行了研究,通过一阶剪切变形理论,建立动力稳定方程,分析了厚度变化对中心裂纹的矩形FGM板动力的稳定的影响。Wu等[12]分析了对边周期动力荷载作用下加强石墨烯板的动力稳定性,得到具有不同条件的石墨烯板的动力不稳定域,给出不同工况的激励荷载的临界频率值。杜菲等[13]分析了集中质量对各向同性板自由振动频率的影响。Darabi等[14]基于薄板大挠度理论,运用Bolotin法建立了层合板的非线性动力稳定方程,分析了不同铺层对板非线性失稳的影响。Sayed等[15]基于时间多尺度扰动法研究了对称交叉层复合材料层合压电板在复合激励下的稳定性。
本文运用特征值法求解四边简支矩形薄板的动力不稳定域和幅频响应,并设计相应的试验模型展开试验研究,应用时域分析法计算无附加质量和携带附加质量板参数共振失稳的临界频率,通过与理论解的对比分析,验证特征值法的正确性,阐明矩形薄板在周期荷载作用下动力失稳时外荷载与板自振频率的变化关系,揭示附加质量对板动力失稳的影响机理,为工程结构中板的设计与运用提供参考。
1 动力方程
图1所示为四边简支矩形薄板在x方向受到周期动力荷载
p(t)=α0Pcr+β0Pcrcosθt
作用的受力简图,其中:α0为静力荷载系数;β0为动力荷载系数;α0Pcr为动力荷载的静力分量;β0Pcr为动力荷载的动力分量;Pcr为板的屈曲荷载。图中:O为直角坐标系的原点;u、v和w分别为板在x、y和z方向的挠度;板的长度、宽度和厚度分别为a、b和h。

图1 板的受力简图
基于Von-Karman薄板大挠度理论,忽略板面内位移u、v与初始缺陷的影响,运用能量变分法分别得到板动力稳定的控制方程:
(1)
(2)
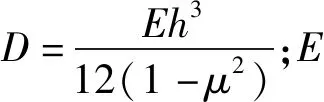
(3)
式中:ρ为单位质量密度;h为板的厚度;Mu为附加质量的大小;δ为狄拉克函数;xu与yu表示附加质量在板上所处的坐标。
假设横向挠度函数和应力函数为:
W(x,y,t)=Wkl(t)ϑk(x)Ψl(y)
(4)
Φ(x,y,t)=
(5)
式中:Wkl和Φpq分别为与时间相关的无量纲函数;ϑk(x)=sin(kπx/a);Ψl(y)=sin(lπy/b)。假设特征函数Xp(x),Yq(y)为:
Xp(x)=cosh(αpx/a)-cos(αpx/a)-
λp(sinh(αpx/a)-sin(αpx/a))
(6)
Yq(y)=cosh(αqy/b)-cos(αqy/b)-
λq(sinh(αqy/b)-sin(αqy/b))
(7)
1-cosαp,qcoshαp,q=0
(8)
(9)
系数αp,αq通过求解式(8)的超越方程得到。
将挠度函数和应力函数代入控制方程中,运用伽辽金法进行积分计算。考虑线性阻尼的作用,得到携带三次方非线性项的Mathieu-Hill方程:
(10)
式中:ξ为阻尼系数;Ω为外荷载作用下板的振动频率;Λ为激发系数;γ为非线性弹性系数。由下式计算得:
(11)
可知,随着附加质量M的增加,γ减小。
将横向挠度函数W周期为2T的解写成傅里叶级数的形式:
(12)
式(12)代入式(10),令sin(nθt/2)和cos(nθt/2)的同类项系数相同,得到关于振幅系数an和bn的线性方程组,令其系数行列式为零,通过整合行列式中的矩阵得到特征方程:


(13)

(14)
(15)
(16)
式中:Cn=nζ/π,Dn=n2,(n=1,3,…,2i-1,i=1,2,…)。
通过求解特征值的方法求解四边简支矩形薄板的动力不稳定域。
当仅研究主要参数共振下的非线性振动时,可以忽略其余谐波的影响,对横向挠度函数进行一阶伽辽金截断,将其代入式(10),令sin(nθt/2)和cos(nθt/2)同类项系数相同,得到关于定态振幅系数an和bn的线性方程组,要使方程组有非零解,则其系数行列式为零,即:
(17)
式中:ζ为阻尼比,通过实验测得;A为板的振动幅值。同样,利用求解特征值的方法,求解得出非线性振动定态振幅的解。i=0、j=1时,求得非线性振动的稳定解;i=1、j=0时,求得非线性振动的不稳定解。
2 试验模型
为验证理论结果的正确性,综合考虑试验设备、边界条件、加载等方面对试验的影响,对长、宽、厚分别为a=1.2 m,b=1.0 m,h=2 mm,密度ρ=2 700 kg/m3,泊松比μ=0.33的各向同性铝制薄板开展动力不稳定性的试验研究。
本试验主要采用德国TIRA激振器与ECON控制系统进行板的激振实验以及丹麦B&K的振动测量系统收集与分析数据。激振系统包括激振器、振动控制器、功率放大器和排风机,测量系统包括传感器、前端模块、电荷放大器和PULSE分析系统。
激振系统的工作原理为:在电脑端设置相关的参数并发出激振指令,指示振动控制器发出相应的振动数字信号,然后功率放大器将振动数字信号进行功率转换,将其转换成相应的电压信号并传输给激振器,激振器在线圈产生的电磁力作用下,控制激振器产生的激振力。当电脑端发出的振动信息超出试验控制值时,固定在激振头上的加速度传感器将该信号反馈给振动控制系统,激振器将会进行自我保护而停止激振试验。
板的振动信号由B&K加速度传感器收集,然后传输给电荷放大器,通过电荷放大器进行功率的转换,将电荷信号转换为电压信号,按振动规律变化的电压信号通过前端模块的储存处理功能转化为笔记本中Lab shop软件能够识别的振动数字信号,最后将板的振动信号进行处理与分析。
试验模型主要由激振台、滑动组件、U1和U3(短边)、U2和U4(长边)、槽形块、开口滚轴、加载梁、铝板等组成。激振台的4个边角用长螺栓和地面连接固定,保证了试验过程中激振台的稳定。如图2所示,4个U型边框内设置U型空间,两端的支撑块设有滑轮槽;铝板的4边嵌入到4个开口滚轴上,每个开口滚轴的两端设置滑轮,滑轮嵌入至U型边框两端支撑块的滑轮槽上并进行固定,从而使开口滚轴可以自由地转动,以此模拟四边简支的边界条件;U1分别与激振器的加载梁和滑动组件连接固定,U3与激振台的挡板连接,并在其底部安装3个滑轮,不仅可以使滑动组件在激振荷载作用下能左右滑动,而且限制滑动组件在加载过程中发生面外位移,影响试验结果;而U2和U4分别通过3个槽形块固定在滑动组件上;为了将激振器产生的集中荷载均匀地施加到板的对边,通过预制加载梁将激振力转换为均布荷载,由于加载梁的刚度很大,在激振力的作用下不产生变形,且其纵截面的中心与开口滚轴的中心平行,确保激振力施加至板横截面的中面上,避免产生偏心荷载影响试验结果。
通过振动控制器设置激振器输出的动力荷载类型为简谐荷载,并设置输出的最大激振力与扫频速率,激振力通过加载梁施加至U1并带动滑动组件向左滑动,由于U3被激振台的挡板限制,使得该激振力同时加载到U3的板边,从而实现对边加载的目的,解决了图1力学模型的模拟。

图2 试验模型
3 自振频率与阻尼比测定
采用丹麦B&K的振动测量系统进行数据的收集与分析。待结构模型安装完成后,将传感器粘贴在铝板测点上下对应的位置,并将各传感器和力锤的信号连接至功率放大器和前端模块,待相关的线连接完成后打开测量软件,然后用力锤敲击滑动组件,将激励同时施加到U1和U3,使铝板产生自由振动,待振动信号收集完毕后,进行OMA分析,得到铝板的自振模态与其对应的自振频率。由测量得到的衰减曲线,利用自由衰减法计算铝板的阻尼比,计算公式为:
(18)
式中:Ati和At(i+j)分别表示第i和第(i+j)时刻的振幅;j为从i时刻起铝板自由振动经过的周期数。图3为无附加质量作用下板的自由振动衰减曲线。

图3 自由振动衰减曲线
4 时域分析法
通过扫频试验发现,当外荷载的激振频率在板自振频率的2倍左右时,板发生强烈的面外竖向振动。为获得板参数共振失稳的临界频率,运用时域分析法观察其在不同激振力下时域曲线周期变化的特点,以此判断板发生参数失稳的时刻,结合扫频范围与扫频速率,通过计算获得不稳定域的临界频率值。
由图4所示时域图可知,板的振动幅值除了发生较大发散的现象之外,A时间段还出现较小突增的情况,其最大的振幅是稳定状态下的2~3倍,但板在该时间段是否发生参数共振失稳或者共振失稳仍不能确定,还需要进一步地分析。由图5可知,A时间段的时域曲线显示板的振动完成了16周循环,即该时间段板的振动频率为16 Hz,表明外荷载的激振频率(16.067 Hz)与板的振动频率近似相等,但与板实测的自振频率(一阶:8.275 Hz,二阶:18.775 Hz)不相等,且与参数共振失稳的特点不同,即在此时间段板未发生参数共振失稳和共振失稳,故该时间段外荷载激振频率未达到致使板发生参数共振失稳的临界值。
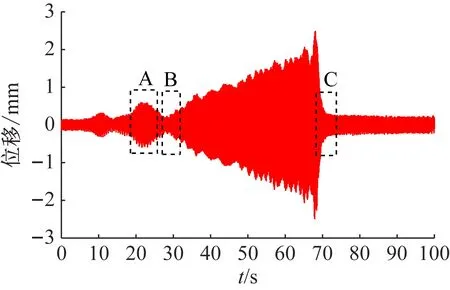
图4 90 N激振力下的时域图

图5 A时间段时域图
由图6可知,在27~30 s的时间段,铝板在1 s的时间里同样只完成了16周循环,即铝板的振动频率约为16 Hz,与激振频率基本一致;在30~33 s的时间段,铝板的振动幅值不断地增加,此时铝板在1 s内完成了8周循环,即铝板的振动频率约为8 Hz,与其自振频率相近,而外荷载的激振频率大约为16 Hz,是铝板自振频率的2倍,且振幅逐渐增加,呈现出参数共振失稳的特征,所以扫频时间30 s为稳定状态过渡至参数共振失稳的临界时间,此时的激振频率对应着板参数共振失稳的上临界频率;同理,由图7可知,在68~70 s的时间段,铝板处于参数共振失稳的状态,而在70~74 s的时间段,铝板的振动频率大约为16 Hz,与外荷载的激振频率基本相等,因此扫频时间70 s为参数共振失稳过渡至暂态振动[1]的临界时间,此时的激振频率对应着板参数共振失稳的下临界频率。
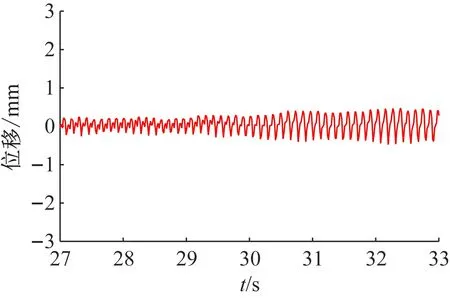
图6 B时间段时域图

图7 C时间段时域图
由上可知,在激振频率不断变化的动力荷载作用下,板发生动力失稳经历了3个主要阶段;当外荷载做功的速率小于板能量耗散的速率时,板处于暂态振动;当外荷载做功的速率大于板能量耗散的速率时,板由暂态振动过渡至参数共振失稳,其振动幅值逐渐增加;此时板发生弹性强化行为,产生硬化效应,相当于增加了板的刚度,板能量耗散的速率逐渐增加,当其值大于外荷载做功速率时,板的振动幅值下降,最终恢复至暂态振动。即板在频率不断变化的外荷载作用下发生动力失稳时,其振动幅值不会一直增加,但当外荷载的频率为上下临界频率区间的某一定值时,板始终处于动力失稳的状态。
5 动力失稳测试
5.1 临界频率确定
在扫频测试的过程中,只考虑简谐荷载中的动力分量,即静力荷载系数α0=0。通过调整不同的激振系数β=β0Pcr/Pmax进行扫频试验,运用时域分析法计算得到铝板发生参数共振失稳的临界激振频率值,其中Pmax是激振器输出的最大激振力,此次试验的最大激振力取100 N。
由OMA分析可知,铝板实测的一阶自振频率为8.275 Hz,由于板发生参数共振失稳的临界频率在板自振频率2倍附近,因此可取板自振频率的2倍作为中心值,根据中心值设置扫频试验的频率范围为15.7~17.7 Hz,并设置扫频试验时的扫频速率为1 Hz/min,设定不同幅值的激振力进行激振实验,通过B&K振动测试系统收集板的振动信号。
当激振系数为0.2时,板的振动幅值未发生变化,即在扫频激振过程中板始终处于稳定的状态,如图8(a)所示。当激振系数分别为0.4、0.6、0.8时,板发生参数共振失稳,振动幅值逐渐增加,如图8(b)~(d)所示。采用时域分析法确定不同激振系数下板发生参数共振失稳的临界时间并结合扫频速率计算上下临界频率值。

(a)0.2
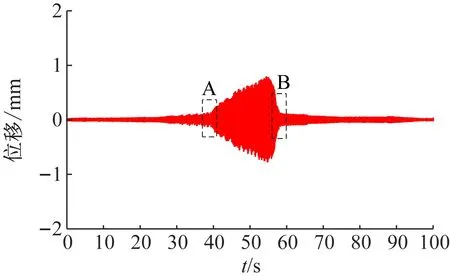
(b)0.4

(c)0.6
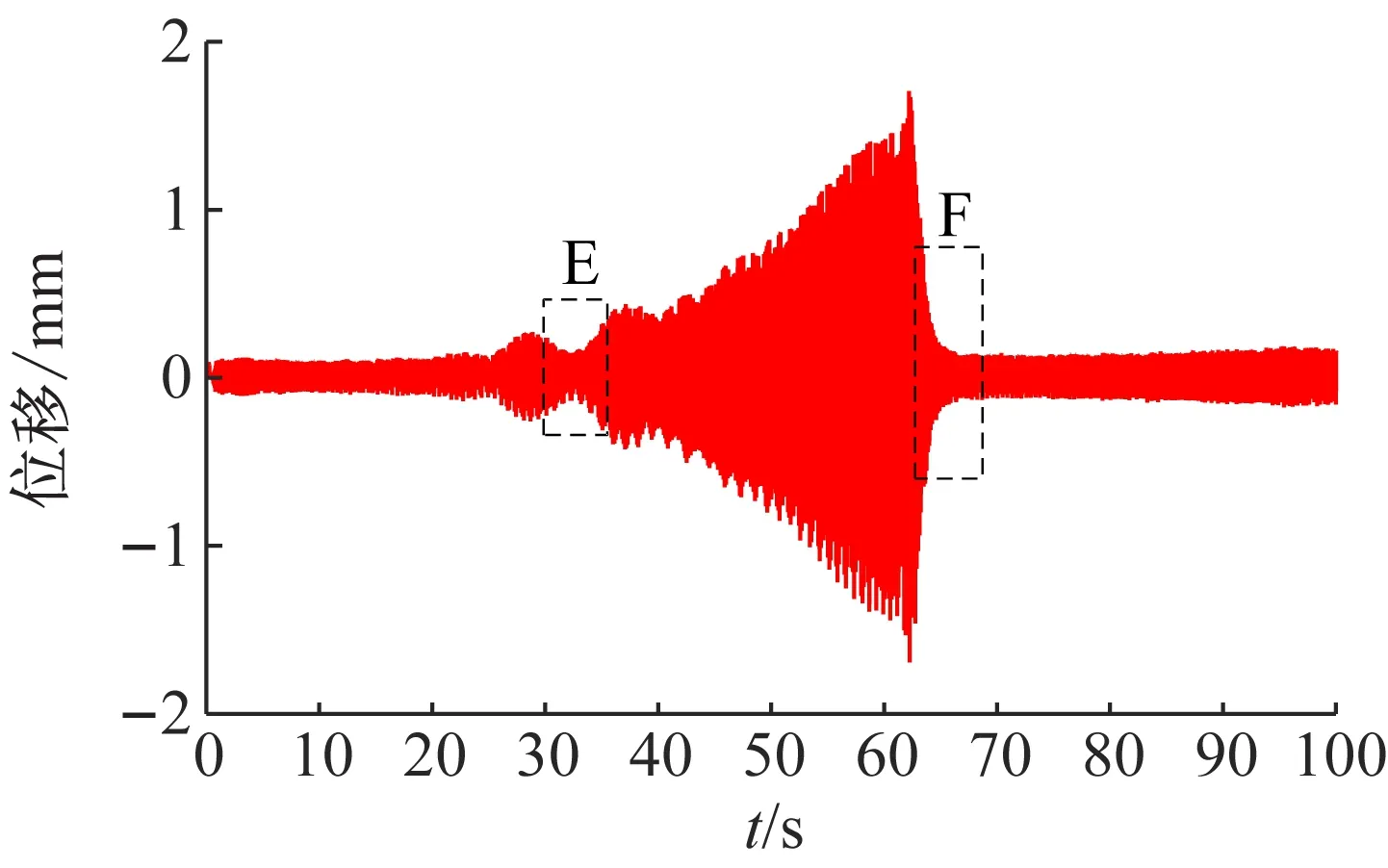
(d)0.8
由图9(a)可知,当激发系数为0.4(40 N)时,板的振动周期在39.6 s时发生变化,由暂态振动过渡至参数共振失稳,此时对应的激振频率为15.7+39.6/60=16.360 Hz,即为该激振系数下板动力失稳的上临界频率;由图9(b)可知,在58 s时板的振动周期再次发生变化,由参数共振失稳过渡至暂态振动,此时对应的激振频率15.7+58/60=16.667 Hz,即为该激振系数下板动力失稳的下临界频率。同理,按照类似的方法可以计算得出其余激振系数作用下无附加质量板以及携带附加质量板发生参数共振失稳时对应的上下临界频率值,并与解析解进行对比,如图10所示。
5.2 幅频响应
为研究面内周期动力荷载作用下板非线性振动的性质,对某一激振系数下的时域曲线进行傅里叶变换,得到该激振系数下板的幅频响应,将其与理论解进行对比,验证板在周期动力荷载作用下的非线性参数振动的正确性。由图11所示的激振系数为0.6时无附加质量板的幅频响应对比可知,试验结果与解析解基本一致,板在周期动力荷载作用下的非线性参数振动产生牵引现象。试验结果发现,当外荷载的激振频率未达到临界频率时,板的实测振动幅值不为零,因为外荷载做功的速率不为零,具有一定的能量使板产生微小的振动;当外荷载的激振频率进入临界频率区域时,板发生参数共振失稳,其振动幅值逐渐增加并表现出强烈的非线性性质,牵引其向大频率方向振动,直到外荷载的激振频率超出临界频率时,板的振动幅值下降,并恢复至稳定的状态。
5.3 附加质量影响
将质量块放置在板的中心位置(a/2,b/2),测试其在不同幅值激振力作用下的瞬态响应,运用时域分析法计算得到对应的临界激振频率。需要指出的是,附加质量作用下板的初始缺陷非常微小可忽略不计。
(a)A时间段

(b)B时间段

(c)C时间段

(d)D时间段

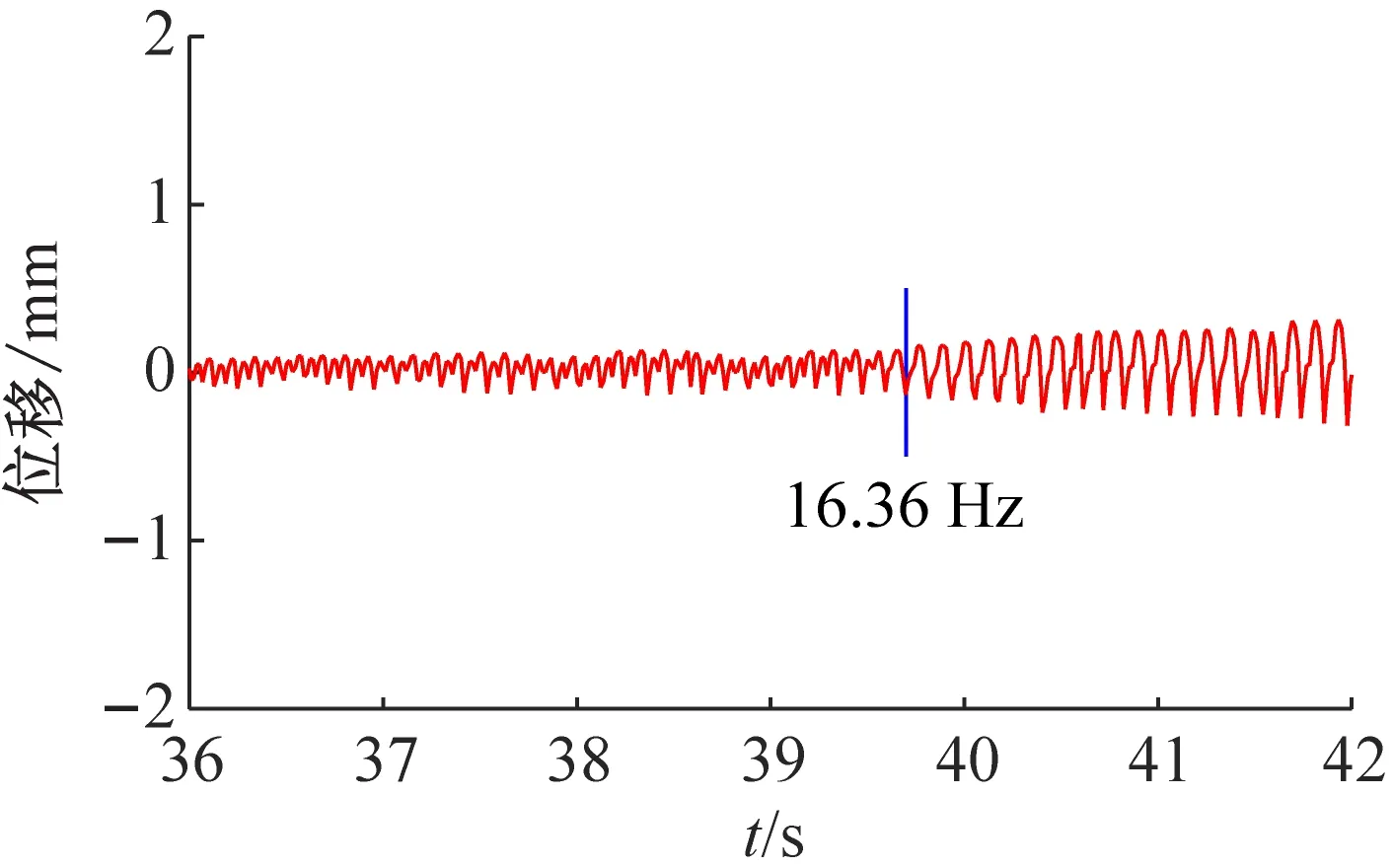
(e)E时间段

(f)F时间段

图10 不同附加质量对临界频率的影响

图11 不同附加质量对幅频响应的影响
将附加质量平均分成两部分,分别粘贴在板上下表面相同的位置处,且在激振试验过程中附加质量始终与板紧密连接,不产生相对位移。由图10所示的临界频率对比图可知,在附加质量的作用下,板的临界激振频率降低,不稳定域宽减小,在相同的激振力作用下,携带附加质量的板先失去稳定。当激振系数小于0.3时,携带附加质量0.25 kg板的临界频率为零,即板在30 N的激振力作用下始终处于稳定的状态,表明在附加质量的作用下,板的阻尼比与其能量耗散的速率增加,导致临界激振系数β相应地增加,在外荷载做功速率不变的情况下,需要更大的激振力才能使板发生参数共振失稳。图11为相同激振系数0.6(60 N)下携带不同附加质量板的幅频响应对比,结果表明随着附加质量的增加,板的非线性弹性系数γ减小,阻尼比增加,但当外荷载克服阻尼做功时,板发生参数共振失稳时的振动幅值增加。
将不同激振系数下扫频试验测试得到的携带不同附加质量板的临界频率与特征值法求解得到的理论不稳定域进行对比发现,实测的临界频率值整体向右偏移,主要的原因是试验无法完全模拟四边简支的边界条件,如边界存在的摩擦增大了边界刚度,使得实测的自振频率较理论值大,但试验与解析解吻合较好,两者的误差均在合理的范围之内,其中最大的误差为1.47%,如表1所示。

表1 临界频率误差对比
6 结 论
(1)通过理论与试验研究分析了对边简谐荷载作用下四边简支矩形薄板的参数共振失稳问题。结果表明,试验与解析解较吻合,证明了特征值法可正确求解板的动力不稳定域与幅频响应。
(2)提出的时域分析法可用于区别板发生参数共振失稳和共振失稳,计算参数共振失稳的临界频率值。
(3)对于对边周期荷载作用下的四边简支矩形薄板,当外荷载的激振频率是板自振频率的两倍左右时,板发生参数共振失去稳定。
(4)板发生参数共振失稳经历了3个主要阶段:当外荷载的做功速率小于板的能量耗散速率时,板处于暂态振动,外荷载的激振频率与板的振动频率相同;当外荷载的做功速率大于板的能量耗散速率时,板由暂态振动过渡至参数共振失稳,其振动幅值逐渐增加,外荷载的激振频率是板自振频率的两倍;当板的能量耗散速率大于外荷载的做功速率时,板的振动幅值下降,最终恢复至暂态振动。
(5)板发生参数共振失稳时,几何非线性限制了板振动幅值的无限增长,并牵引其往大频率方向振动。
(6)附加质量降低了板的自振频率,增大了板的阻尼比和振幅,减小了板的动力不稳定域宽,在相同激振力作用下携带附加质量的板先失去稳定,且随着附加质量的增加,板发生参数共振失稳的临界频率逐渐减小,临界激振系数逐渐增加。

